W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 24

Szczegóły: Kategoria: Zadania z fizyki; Opublikowano: wtorek, 29, grudzień 2015 17:54; Autor : Janusz Szcząchor; O mnie:; Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 3.118, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

Ze szczytu równi pochyłej zsuwa się niewielki ciężarek o masie m = 3 kg (3.38). Na końcu równi uderza o ścianę prostopadłą do kierunku ruchu, odbija się bez straty energii i porusza się pod górę równi. Na jakiej wysokości zatrzyma się ciężarek, jeżeli kąt α = 30°, AC = 3 m, a współczynnik tarcia wynosi f = 0,25?

Rozwiązanie - Analiza treści zadania

Jest to pierwsze zadanie w moim poradniku poświęcone zjawisku tarcia. Na chwilę pomińmy zjawisko tarcia i zastanówmy się jak wyglądałby w tak zmienionej sytuacji ruch naszego ciężarka?

Jasne jest, że tarcie wywołuje stratę energii mechanicznej, której część zamienia się wtedy na ciepło. Gdyby nie było tarcia, to nie byłoby straty energii, a zatem mielibyśmy w zadaniu bezstratne procesy przemiany energii potencjalnej ciężkości w energię kinetyczną i na odwrót. Zatem nie ulega wątpliwości, że wtedy ciężarek po odbiciu się od przeszkody zatrzymałby się na tej samej wysokości z jakiej zaczął się zsuwać.

Z treści zadania jasno wynika, że mamy tutaj do czynienia z tarciem kinetycznym, bo ciężarek się porusza. Straty energii mechanicznej przejawiają się w tym, że ciężarek wolniej się rozpędza i nie osiągnie przed zderzeniem ze ścianą prędkości, którą by osiągnął, gdyby tarcia nie było. Po bezstratnym odbiciu się od przeszkody ciężarek poruszając się w górę równi dalej traci energię. Dlatego nie osiągnie on pierwotnej wysokości, z której zaczął się zsuwać.

Jeżeli chodzi o typy ruchu jakimi się porusza ciężarek, to mamy dwa :

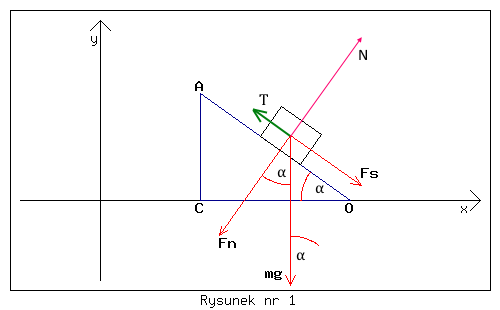
gdy ciężarek zsuwa się w dół, to porusza się ruchem jednostajnie przyspieszonym bez prędkości początkowej, przy czym składowa styczna siły ciężkości wywołująca ruch jest zmniejszona o siłę tarcia, patrz rysunek nr 1;
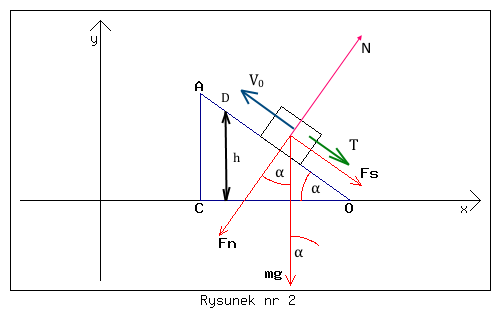
gdy ciężarek porusza się w górę równi, to porusza się ruchem jednostajnie opóźnionym z prędkością początkową v₀, przy czym teraz siły hamujące są dwie, styczna siły ciężkości oraz siła tarcia, patrz rysunek nr 2.

Rozwiązanie - Obliczenia

Aby obliczyć na jakiej wysokości zatrzyma się ciężarek musimy obliczyć drogę jaką on przebędzie od momentu odbicia się od przeszkody do chwili zatrzymania się. Wtedy korzystając z odpowiedniej funkcji trygonometrycznej obliczymy wartość pożądanej zmiennej. Jednak z uwagi na to, że ciężarek w górę równi porusza się ruchem jednostajnie opóźnionym, to najpierw musimy obliczyć prędkość początkową w tym ruchu. Ponieważ ciężarek odbija się bez straty energii więc jego prędkość początkowa w ruchu opóźnionym jest równa prędkości z jaką ciężarek uderza w przeszkodę. A ta z kolei jest równa prędkości końcowej jaką ciężarek osiągnie w ruchu w dół równi.

W typowych zadaniach zwykle podaje się czas, przez jaki ciało porusza się ruchem jednostajnie przyspieszonym. Wtedy prędkość ciała jest dana następującym wzorem

v(t) = at + v₀. (1)

U nas v₀ = 0. Jednak czas ruchu nie jest podany, a musimy go sami wyliczyć korzystając z faktu, że ciężarek przebędzie drogę całego stoku równi. Oznaczmy zatem jako l długość stoku równi (czyli odcinek AO) i korzystając z rysunku nr 1 możemy napisać, że

sinα = AC/l,

czyli

l= AC/sinα. (2)

Ponieważ ruch w dół równi jest bez prędkości początkowej, więc l jest dane zwykłym wzorem na drogę w ruchu jednostajnie przyspieszonym, czyli

l = at²/2 .

Zatem

t = (2l/a)^½. (3)

Podstawiając (3) do (1), uwzględniając, że v₀ = 0 oraz skracając pierwiastek kwadratowy z przyspieszenia a otrzymujemy, że

v(t) = (2al)^½. (4)

Teraz musimy przypomnieć, że siła tarcia jest dana jako

T = fN , (5)

gdzie f - współczynnik tarcia kinetycznego, a N - to siła nacisku podłoża na ciało, czyli na nasz ciężarek. Ponieważ ciężarek nie porusza się wzdłuż prostej prostopadłej do równi, więc nacisk równi N jest równy co do wartości składowej F_n siły ciężkości ciężarka prostopadłej do równi (patrz rysunek nr 1). Ponieważ F_n= mgcosα, zatem

T = fmgcosα . (6)

W końcu, II zasada dynamiki Newtona dla ruchu ciała w dół równi ma postać ( patrz rys. nr 1)

ma = F_s - T,

czyli przyspieszenie ciężarka jest dane zależnością (F_s = mgsinα)

a = g(sinα - fcosα). (7)

Zatem podstawiając (7) do (4) otrzymujemy wartość poszukiwanej przez nas prędkości końcowej w ruchu w dół równi jako

v(t) = [2lg(sinα - fcosα)]^½. (8)

Dla ruchu w górę równi, jak wcześniej to ustaliliśmy jest to prędkość początkowa, dlatego do dalszych obliczeń zmieniamy oznaczenia i teraz mamy

v₀ = [2lg(sinα - fcosα)]^½ . (9)

Po odbiciu się od przeszkody, w ruchu w górę równi, ( patrz rysunek nr 2 ) II zasada dynamiki Newtona przyjmuje formę

ma = F_s + T,

a zatem teraz przyspieszenie (ujemne) ciężarka to

a = g(sinα + fcosα). (10)

Teraz, aby obliczyć jaką drogę przebędzie ciężarek w górę równi musimy najpierw znaleźć czas po jakim prędkość ciała spadnie do zera. Prędkość ciała w ruchu jednostajnie opóźnionym jest dana wzorem

v(t) = v₀ - at₁. (11)

Tu dla odróżnienia, w tym ruchu czas oznaczyłem jako t₁. Podstawiając v(t) = 0 obliczamy z (11), że czas t₁ wynosi

t₁ = v₀/a. (12)

Na razie jeszcze, dla wygody rachunków, jawnie nie podstawimy v₀, lecz prowadzimy obliczenia dalej. Wzór na drogę w ruchu jednostajnie opóźnionym ma postać

s = v₀t₁ - a(t₁)²/2. (13)

Podstawiając (12) do (13) i dokonaniu uproszczeń otrzymujemy, że

s = (v₀)²/2a . (14)

Teraz już można wygodnie podstawić do (14) wzór (9), jak i (10). Po wykonaniu kwadratu oraz skróceniu w liczniku i mianowniku 2g otrzymujemy, że droga ciężarka w górę równi wyrażona już przez prawie same dane zadania za wyjątkiem l, to

s = [l(sinα - fcosα)]/(sinα + fcosα) . (15)

Korzystając z rysunku nr 2 widzimy, że wysokość h, na jaką się wzniósł ciężarek, dzięki przyrównaniu DO = s, to

h = s sinα . (16)

Teraz podstawiamy za s wzór (15), za l wzór (2), skracamy sinusy α ( oczywiście tylko te, które można ), a także dzielimy licznik i mianownik przez cosα, i w końcu otrzymujemy ostateczny wynik, że

h = [AC(tgα - f)]/(tgα + f) . (17)

Podsumowanie

W przedstawionym rozwiązaniu umieściłem szczegółowe wyprowadzenia wzorów. Uznałem, że niektórym z czytelników może się to przydać mimo, że to są dość proste wzory. Moim zdaniem na tym poziomie powtórek nigdy dość.