Rachunek różniczkowy i całkowy w fizyce szkolnej - część 7

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: czwartek, 18, maj 2015 23:25

Autor : Janusz Szcząchor

Zadanie 1.30, M.S.Cedrik i inni - "Zadania z fizyki", PWN, Białystok 1975

Dowieść, że przy braku oporu powietrza maksymalny zasięg rzutu ukośnego uzyskuje się dla kąta wyrzutu (tzn. kąta pomiędzy poziomem i kierunkiem prędkości początkowej) równego 45°. Zadanie rozwiąż wykorzystując rachunek różniczkowy.

Rozwiązanie

Rzut ukośny jest przykładem ruchu na płaszczyźnie. Jeżeli założymy, że pomijamy opór powietrza, to ciało rzucone wykonuje ruch złożony, który możemy rozłożyć na dwa ruchy:

poziomo

- ruch jednostajnie prostoliniowy z prędkością v_x = v₀ cosθ, gdzie v₀ to prędkość początkowa ciała, a θ to kąt pod jakim rzucono ciało,

pionowo

- ruch jednostajnie opóźniony prostoliniowy, gdzie opóźnienie jest równe g, a prędkość początkowa, to v_y = v₀ sinθ.

Mając to ustalone możemy wypisać równania ruchu, wzdłuż osi X

x = v₀t cosθ , (1)

oraz wzdłuż osi Y

y = v₀t sinθ - gt²/2 . (2)

Obydwa równania podają łącznie równanie ruchu rzuconego ciała w formie parametrycznej, gdzie parametrem jest czas.

Jeśli uda nam się wyeliminować parametr t z równań (1) i (2), to otrzymamy równanie ruchu ciała rzuconego w formie uwikłanej. Takie równanie wiąże bezpośrednio zmienne y i x ze sobą, a jego wykresem w płaszczyźnie xy jest tor ruchu ciała.

Zauważmy, że z (1) możemy wyliczyć czas, tj.

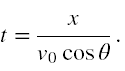
Podstawiając powyższe do (2) mamy

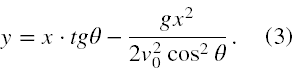
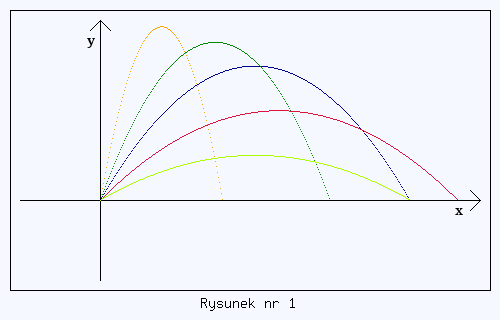
Aby zobaczyć jak wygląda tor ruchu dany równaniem (3) można przejść na stronę poświęconą animacji rzutu ukośnego lub przyjrzeć się poniższemu rysunkowi nr 1. Przedstawiono na nim 5 wykresów zależności y(x) z równania (3) dla kątów wyrzutu równych:

1. 80° (kolor pomarańczowy),
2. 70° (kolor zielony),
3. 60° (kolor niebieski),
4. 45° (kolor czerwony),
5. 30° (kolor żółty).

Parametr g/2v₀² z równania (3) jest dla wszystkich wykresów identyczny.

Powstaje teraz pytanie co to jest zasięg rzutu ukośnego? Dość chyba oczywistym jest, że chodzi tu o maksymalną dopuszczalną wartość położenia na osi x jakie ciało może osiągnąć, którą oznaczymy jako x_max. Jak obliczyć tę wielkość? W tym celu jest konieczne znalezienie równania na x_max, a do tego potrzebne jest ustalenie odpowiedniego warunku określającego, kiedy z taką sytuacją będziemy mieli do czynienia.

Można zauważyć, że gdy ciało kończy ruch, to z pewnością y = 0, a odpowiadająca tej wartości y wartość x, to właśnie x_max. Jednak ta sama sytuacja też zachodzi dla punktu początkowego ruchu, tj. gdy x = 0. Tę sytuację należy odrzucić. W tym celu równanie (3) można przepisać wyłączając x przed nawias i otrzymujemy

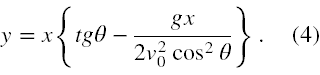
Przyrównując w (4) zmienną y do zera otrzymujemy, że albo x = 0, albo klamrowy nawias jest równy 0. Z uwagi na powyższe widzimy, że jedynym pożądanym rozwiązaniem jest wniosek wynikający z zerowania się nawiasu klamrowego, czyli

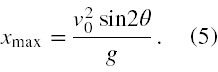
Tutaj po drodze skorzystaliśmy z tożsamości trygonometrycznej sin2θ = 2sinθcosθ. A zatem widać, że x_max zależy od kąta wyrzutu poprzez funkcję sin2θ.

Elegancki i uniwersalny sposób na znalezienie wartości θ, przy której x_max ma wartość największą, to skorzystanie z rachunku różniczkowego.

Zgodnie z tw. Fermata [1] warunkiem koniecznym na to, aby x_max jako funkcja kąta θ osiągała dla pewnej wartości tego kąta ekstremum jest, aby dla tej wartości kąta x_max miała względem θ obustronną pochodną o wartości skończonej i równej 0. Ponieważ funkcja sin2θ jest funkcją różniczkowalną, więc wymagania tego twierdzenia co do samego faktu posiadania przez funkcję pochodnej mamy spełnione. Stąd otrzymujemy równanie

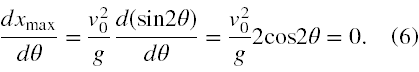
Pochodną obliczyliśmy zgodnie z regułą dla funkcji złożonej. Kosinus ma pierwszy punkt zerowy dla π/2, czyli 90°. Stąd

2θ = π/2 ,

czyli

θ = π/4 .

A zatem widzimy, że dla wartości θ = π/4 x_max może mieć ekstremum. Pozostaje zbadanie czy ma i czy jest to maksimum, czy też minimum?

Zgodnie z [2] warunkiem dostatecznym na to, aby x_max jako funkcja kąta θ miała dla θ = π/4 maksimum jest, żeby dla tej wartości kąta istniała druga pochodna x_max względem θ i była ona ujemna. Zatem

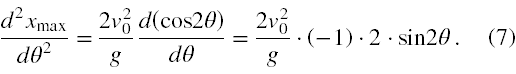
Funkcja sin2θ dla θ = π/4 (czyli sinus 90°) jest równa 1. Biorąc pod uwagę minus z różniczkowania oraz fakt, że pozostałe wyrażenia w (7) są dodatnie widzimy, że całe wyrażenie (7) dla θ = π/4 jest ujemne. W związku z tym mamy dowód na to, że dla kąta wyrzutu równego 45° zasięg rzutu ukośnego jest maksymalny.

LITERATURA

[1] G.M.Fichtenholz, Rachunek Różniczkowy i Całkowy,Tom I , PWN, W-wa 1978, § 109, § 134;
W.Leksiński, B.Macukow, W.Żakowski, Matematyka w zadaniach dla kandydatów na wyższe uczelnie, WNT, W-wa 1981 §9.5.Ekstrema funkcji.

[2] G.M.Fichtenholz, Rachunek Różniczkowy i Całkowy,Tom I , PWN, W-wa 1978, § 137.
W.Leksiński, B.Macukow, W.Żakowski, Matematyka w zadaniach dla kandydatów na wyższe uczelnie, WNT, W-wa 1981 §9.5.Ekstrema funkcji.