Rachunek różniczkowy i całkowy w fizyce szkolnej - część 4

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: sobota, 16, styczeń 2016 11:25

Autor : Janusz Szcząchor

zadanie nr 3.30 , Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

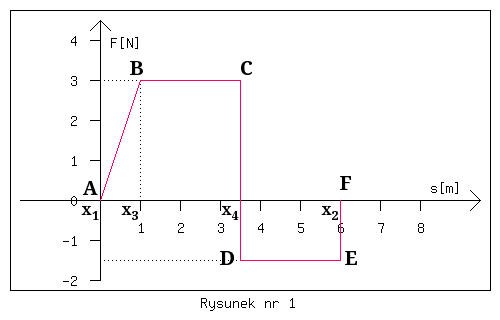
Oblicz pracę wykonaną przez siłę F, której zależność od przesunięcia podano na wykresie 3.7 (tutaj rysunek nr1) . Wektory siły i przesunięcia są równoległe. Zadanie rozwiąż używając rachunku całkowego.

Rozwiązanie

Jak wynika z wykresu na rysunku nr 1 (patrz poniżej) siła F nie jest funkcją stałą jako funkcja przesunięcia i dlatego ma tutaj sens zastosowanie całkowego wzoru na pracę. Wprawdzie można tu pracę policzyć bez rachunku całkowego, lecz charakter siły F jako funkcji s szczególnie, moim zdaniem, daje tutaj wyjątkową okazję do przedstawienia wyjaśnień co do takich zagadnień, które mogą stanowić poważny problem dla początkujących użytkowników rachunku całkowego w fizyce.

Przypomnijmy zatem, że całkowitą pracę wykonaną przez siłę F podczas przemieszczania się ciała z położenia x₁ do położenia x₂ można zapisać w formie

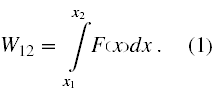
(Ograniczyłem się tutaj do pracy wykonanej tylko wzdłuż jednej osi, ponieważ wektory siły i przesunięcia są równoległe w tym zadaniu.)

Jednak zastosowanie bezpośrednie wzoru (1) do funkcji F(x) z rysunku nr 1 jest niemożliwe, a to dlatego, że funkcja ta nie jest funkcją, którą można przedstawić analitycznie w tym przedziale zmienności, tj. podać w formie jednego wzoru algebraicznego. Ponadto drugim powodem jest to, że funkcja F(x) jest nieciągła. Stąd potrzeba pewnych wyjaśnień.

Zgodnie z (¹) każda funkcja ograniczona o skończonej ilości punktów nieciągłości jest całkowalna. A taką jest tutaj funkcja F(x).

Z kolei całka oznaczona zgodnie z (²) ma tę własność, że jeżeli jest dany ciąg liczb a,b,c, ...,k,l napisanych w dowolnej kolejności, to zachodzi wzór :

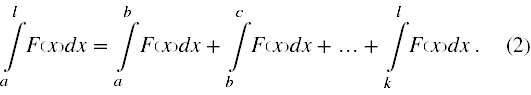
Dzięki temu możemy sprowadzić obliczanie całki (1) do zsumowania całek, z których każdą będzie można już policzyć analitycznie. Osiągniemy to poprzez podział przedziału <x₁,x₂> na takie podprzedziały, w każdym z których będzie można wyrazić siłę F(x) wzorem algebraicznym.

Przechodząc do sytuacji tego zadania wyrażonej na rysunku nr 1 (patrz niżej) można stwierdzić, że:

1. na odcinku AB definiując współczynnik α można wyrazić F(x) jako funkcję liniową przemieszczenia, tj. F(x) = 3xα, gdzie α=N/m,
2. na odcinku BC F(x) = 3N,
3. na odcinkach CD i EF praca jest równa 0, bo przemieszczenie jest równe 0, a wartość siły choć nie jest ustalona, ale jest ograniczona,
4. na odcinku DE F(x) = -1.5N.

Dlatego oznaczając punkty x₁, x₂, x₃ i x₄ (patrz rysunek nr 1) możemy przepisać wzór (1) w zastosowaniu do tego zadania jako

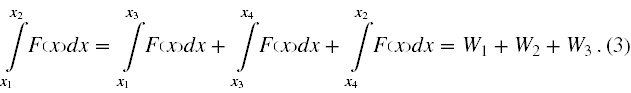
A więc liczymy.

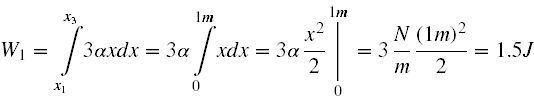
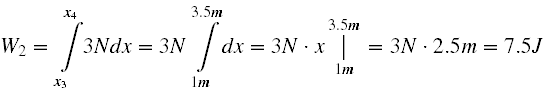
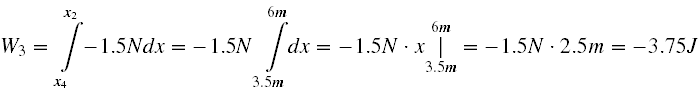
Łącznie W = W₁ + W₂ + W₃ = 1.5J + 7.5J - 3.75J = 5.25J .

LITERATURA

¹ G.M. Fichtenholz - Rachunek różniczkowy i całkowy, tom II, §298 Klasy funkcji całkowalnych

² W.I.Smirnow - Matematyka Wyższa Tom I , § 9.94 Podstawowe własności całki oznaczonej