W jaki sposób Schrödinger wyprowadził swoje niestacjonarne równanie?

Szczegóły

Kategoria: Publikacje naukowe

Opublikowano:piątek, 19 luty 2021 17:30

Autor : Janusz Szcząchor

How did Schrödinger derive his nonstationary equation?

Abstract: The article presents the second, original method of deriving the stationary and non-stationary Schrödinger equations. Its starting point is Hamilton's idea of the equivalence of Jacobi and Fermat principles. Then Schrödinger, assuming that matter is de Broglie waves, calculates their phase velocity on the basis of comparing the velocity of matter to the group velocity of these waves. Finally, noticing that de Broglie waves are longitudinal ones uses the wave equation for longitudinal waves in a fluid to get his both equations.

1. Wstęp

Jakiś czas temu napisaliśmy artykuł „Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 2” [11], oparty na [1], gdzie jest opisany pierwszy sposób, w jaki Schrödinger wyprowadził swoje równanie stacjonarne. Jednak jak wynika z jego kolejnej pracy [2], mimo sukcesu w wyjaśnieniu widma atomu wodoru, Schrödinger nie był całkowicie zadowolony ze swoich rezultatów. Zapewne powodem tego była niemożność wyprowadzenia równania niestacjonarnego.

Punktem startowym tamtej metody jest równanie Hamiltona-Jacobiego, gdy czas nie występuje w funkcji Hamiltona, a funkcja działania S zależy od funkcji falowej Ψ. Jednak nie da się tą metodą podać postaci niestacjonarnego równania kwantowego. Schrödinger zmuszony był poszukać nowego rozumowania, które zawarł w [2], jak i [3].

W tym artykule również starałem się przedstawić wiernie idee Schrödingera, jednak w paru miejscach musiałem niejako „wyprostować jego sformułowania i myśli”, albowiem wypowiada się w nich w sposób zbyt intuicyjny, co u osób nie zajmujących się zawodowo fizyką, zwłaszcza kwantową, mogłoby prowadzić do niezrozumienia tekstu. Niektóre fragmenty natomiast skracałem, zwłaszcza gdy dotyczyły one faktów dzisiaj dość oczywistych.

2. Druga metoda wyprowadzenia równania stacjonarnego

Punktem wyjścia drugiej metody Schrödingera wyprowadzenia niestacjonarnego równania kwantowego jest zasada Jacobiego. Wyjaśnimy szczegółowo o co tu chodzi (naszym przewodnikiem będzie tu [3], jak i [4] ¹).

Niech układ fizyczny składa się, mówiąc językiem mechaniki klasycznej, z jednego punktu materialnego mającego masę m i ewentualnie ładunek elektryczny q. Natomiast w języku fizyki kwantowej będziemy mieć na myśli cząstkę elementarną o masie m i ładunku elektrycznym q. Dalej niech układ znajduje się w przestrzeni nieograniczonej, w której panuje pole oddziaływania zachowawcze, tzn. dla tego układu energia mechaniczna, czyli suma jego energii kinetycznej i potencjalnej jest stała, i równa E (²).

Załóżmy, że teraz układ ma za zadanie przemieścić się z punktu A do punktu B, rysunek poniżej. Powstaje pytanie, jak wskazać (wzorem matematycznym) wzdłuż której krzywej łączącej te dwa punkty układ będzie się poruszał?

Podstawowa odpowiedź jest taka, że musimy znać wzór matematyczny na siłę działającą na układ w tym polu, podstawić ją do II zasady dynamiki, rozwiązać równanie Newtona. Następnie wybierając odpowiednie warunki początkowe wybrać taką krzywą, dla której ciało w chwili t₀ będzie się znajdować w punkcie A, a w chwili t₁ będzie się znajdować w punkcie B. Jako rozwiązanie otrzymamy wektor położenia układu, którego współrzędne będą funkcjami czasu. Jednak można się pokusić o coś alternatywnego.

Wyobraźmy sobie, że chcemy wyrazić prawa mechaniki nie posługując się funkcjami zależnymi od czasu. W tym celu przyjmijmy, że będziemy wyrysowywać różne krzywe łączące punkty A i B oraz mierzyć ich długość, a następnie szukać, która z tych krzywych jest najkrótsza. Taka mniej więcej jest idea zasady Jacobiego, której matematyczne sformułowanie ma następującą postać.

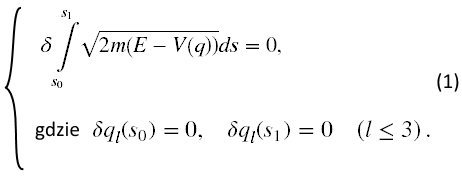
A zatem załóżmy, że krzywa łącząca punkty A i B wyrysowana na czerwono to krzywa rzeczywista, zgodna z prawami fizyki, po której układ fizyczny poruszając się ma całkowitą energię mechaniczną równą E. Natomiast wyrysowana na niebiesko to przykład dowolnej innej krzywej, zwanej krzywą porównawczą, po której chcielibyśmy, żeby układ hipotetycznie mógłby się poruszać też od punktu A do B i mając tą samą energię całkowitą, rysunek poniżej.

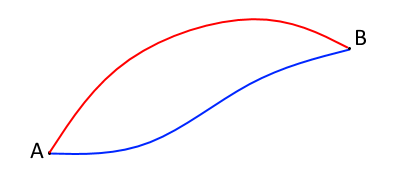
Zmienna s użyta w (1), to długość krzywej. Jednak wartość początkową tej zmiennej s₀ oraz końcową s₁ należy traktować trochę symbolicznie. Oznaczają one, że wszystkie krzywe zaczynają się w tym samym punkcie A, a kończą w punkcie B i mają w tych punktach te same współrzędne q_l. Mówi o tym druga linijka wzoru (1).

Natomiast pierwsza linijka (1) mówi o tym, że dla każdej krzywej liczymy całkę znajdującą się pod znakiem δ, czyli każdą krzywą dzielimy na malutkie kawałki o bardzo małej długości ds, wymnażamy długość takiego kawałeczka przez wartość pierwiastka √(2m(E − V (q))) dla wartości współrzędnej q_l takiego kawałeczka i te iloczyny sumujemy dla każdej krzywej z osobna. Krzywą, po której odbywa się ruch rzeczywisty jest ta, dla której wartość tej sumy jest ekstremalna, najczęściej najmniejsza.

Matematycznie formułujemy to w ten sposób, że dla ruchu rzeczywistego i tylko dla ruchu rzeczywistego pierwsza wariacja działania Maupertuis jest równa 0 (działaniem jest wartość tej całki).

Teraz możemy wrócić do myśli Schrödingera. W pracach [2] i [3], przypomniał on ideę Hamiltona o tym, że równanie (1) ma dużo wspólnego z zasadą Fermata w optyce ([5] ³), która w naszych oznaczeniach przyjmuje postać

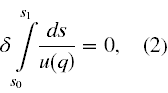
gdzie u(q), jest lokalną prędkością światła. Przyjmując, że tutaj punkty A i B znajdują się w tych samych miejscach co poprzednio (a jedynie pole potencjalne zniknęło, w zamian za to pojawił się niejednorodny ośrodek) mówi ona, że w ośrodku niejednorodnym optycznie rzeczywiste promienie świetlne biegną tak, aby przebyć drogę od punktu A do punktu B w czasie możliwie najkrótszym.⁴ Zdaniem Schrödingera oba prawa stałyby się identyczne, gdyby 1/√(2m(E − V (q))) można było zinterpretować jako prędkość (miało wymiar prędkości).

Sprawdźmy jaki wymiar ma ta wielkość

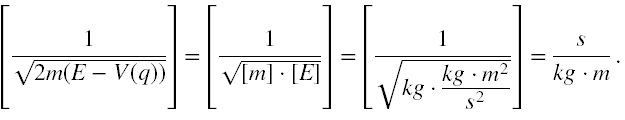
Gdyby jednak w liczniku zamiast jedynki stało coś co ma wymiar energii, czyli kg·m²/s², to cały ułamek miałby wymiar prędkości. Ale pierwsze równanie w (1) możemy podzielić stronami przez stałą C (o wymiarze energii). Wtedy różniczka ds, będzie podzielona przez wielkość, którą za Schrödingerem też oznaczamy jako

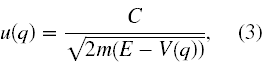
gdzie stała C musi być niezależna od q, ale może zależeć od E. Stąd jak podkreśla Schrödinger: „W ten sposób stworzyliśmy myślowy obraz ośrodka optycznego, w którym zbiór dopuszczalnych promieni świetlnych pokrywa się ze zbiorem dynamicznych orbit punktu materialnego (o masie) m o zadanej energii (E) poruszającego się w polu siły V(q).”. Ponownie oderwijmy się od myśli Schrödingera i spróbujmy wyjaśnić czytelnikowi o co w tym wszystkim chodzi.⁵

Jak się można dowiedzieć ze wspomnień Diraca [6], Schrödinger choć wykorzystywał teorię orbit Bohra do badania widm, to jednak miał wiele do niej zastrzeżeń. Gdy w 1924 roku de Broglie wysunął hipotezę, że z ruchem swobodnej cząstki materii (np. elektronu) jest stowarzyszona specjalna fala ją pilotująca postanowił uogólnić tę teorię dla przypadku cząstek związanych

Jednak trzeba wiedzieć, że podstawą teorii de Broglie’a był postulat, że skoro istnieje dualizm falowo-korpuskularny dla światła (czyli fotonów), to i na odwrót tak samo powinno być dla materii. Stąd jeśli mamy dwa ⁶ poziomy teorii opisu światła, czyli optyka klasyczna i optyka falowa, to tak samo powinno być dla materii, czyli mechanika klasyczna i mechanika falowa (kwantowa).

Zatem powinny być między tymi teoriami ścisłe podobieństwa matematyczne, jak i ideowe. Tym samym odpowiednikiem elektronu powinien być foton. Skoro foton można traktować raz jako cząstkę „klasyczną” o energii E = hf ⁷ i pędzie p = hf/c , a drugi raz jako promień świetlny (zasada Fermata), to elektron też powinno raz dać się opisać jako cząstkę „klasyczną” (równania Newtona), a drugi raz jako „promień materii” (zasada Jacobiego). Powróćmy do myśli Schrödingera

Widzieliśmy, że wielkość u(q) daną wzorem (3) można rzeczywiście traktować jako jakąś prędkość, lecz zależy ona nie tylko od położenia, ale także od energii E punktu materialnego. Jeżeli przypomnimy sobie, że zgodnie z hipotezą de Broglie’a z każdą cząstką materialną o energii E jest stowarzyszona fala pilotująca (funkcja falowa) o częstotliwości f wynikającej ze wzoru

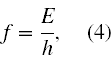
to widzimy, że mamy do czynienia ze zjawiskiem dyspersji, czyli zależnością prędkości rozchodzenia się „fal materii” w naszym niejednorodnym ośrodku od ich częstotliwości. Powstaje pytanie, czy i na ile u(q) ma coś wspólnego z prędkością naszego punktu materialnego (elektronu)?

W tym celu zauważmy, że

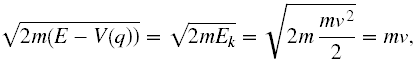
czyli to pęd cząstki. Zatem prędkość cząstki

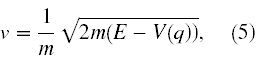
jest odwrotnie proporcjonalna do u(q) we wzorze (3). Na szczęście jest wyjaśnienie tej sprzeczności, wskazał je Schrödinger, ale aby to przedstawić musimy zrobić dłuższą dygresję o falach.⁸

Na samym początku zakładamy, że cząstkę materialną (elektron) reprezentuje fala de Broglie’a, która zachowuje się podobnie jak fala świetlna, czyli gdy zaniedbujemy zjawiska dyfrakcji i interferencji podlega takim prawom, jakie światło w optyce geometrycznej.

Jednak prędkość u(q) w zasadzie Fermata, to prędkość fazowa światła (równa zawsze lokalnej wartości c). W ośrodku dyspersyjnym dla każdej częstotliwości f prędkość v(f) jest inna, bo zależy od współczynnika załamania n(f) ośrodka, który jest różny dla różnych częstotliwości światła. Zatem wszystko byłoby w porządku, gdyby u(q) dana wzorem (3) byłaby prędkością fazową fal de Broglie’a dla materii. Ale czy jest?

Ze szkoły średniej powinieneś wiedzieć, że matematycznie falę harmoniczną opisujemy funkcją falową postaci

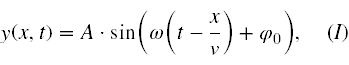
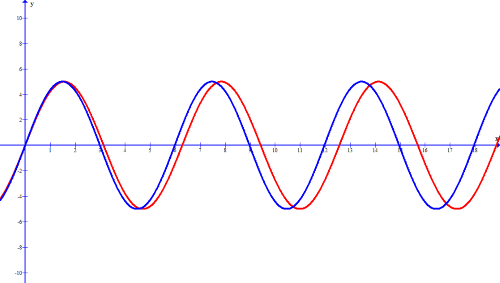
gdzie częstotliwość fali f = ω/2π. Taka fala jest monochromatyczna i nieskończona. Niestety w przyrodzie nie istnieją takie fale. Rzeczywiste fale są skończone i co ważniejsze są sumą wielu fal monochromatycznych o częstościach (kołowych) ω pochodzących z pewnego wąskiego przedziału (ω+∆ω,ω−∆ω). Dla wygody oznaczmy ω/v jako k, czyli liczbę falową, a następnie dodajmy do siebie dwie fale płaskie o dwóch bliskich częstościach kołowych ω i ω + ∆ω, oraz tych samych amplitudach, rysunek poniżej.

Wynik takiej superpozycji to

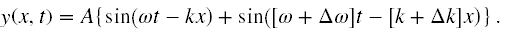
Korzystając ze wzorów trygonometrycznych (suma sinusów) możemy falę tę przekształcić do postaci, którą łatwiej zinterpretować

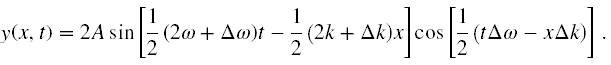
Ponieważ zakładaliśmy, że ∆ω jest bardzo małe (a zatem i ∆k), więc 2ω + ∆ω ≈ 2ω oraz 2k + ∆k ≈ 2k. Wzór na naszą superpozycję zatem przyjmuje postać

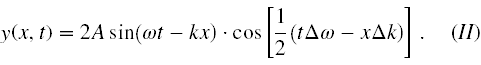
Przy przyjętych przez nas założeniach wielkość t∆ω − x∆k jest bardzo bliska 0, zatem kosinus w (II) bardzo wolno oscyluje i przez stosunkowo długi czas jest bliski 1. Stąd fala dana wzorem (II) zawiera w sobie część szybko zmieniającą się, czyli sinus (narysowany linią ciągłą, rysunek poniżej) oraz wolno zmieniającą się, czyli cosinus tworzący tzw. zwaną obwiednię (linia przerywana, rysunek poniżej).

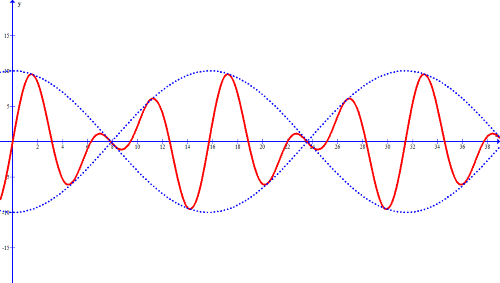
Aby ustalić z jaką prędkością porusza się dana fala musimy śledzić punkt fali o wybranej fazie. Matematycznie oznacza to, że fazę fali musimy przyrównać do dowolnej stałej. Dla fali szybszej, sinusoidalnej (oznaczonej powyżej na rysunku na czerwono) mamy

ωt - kx = const.

Ponieważ poszukujemy prędkości tej fazy, czyli związku między x i t, więc różniczkujemy powyższe stronami i jest

ωdt - kdx = 0,

zatem prędkość fazowa fali (II), to

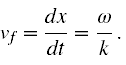
Powtarzając to samo dla cosinusa (oznaczony powyżej na rysunku na niebiesko) otrzymujemy

Δωdt - Δkdx = 0,

czyli prędkość grupowa fali (II), to

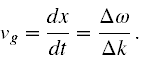
Jeżeli ∆k i ∆ω(zależy od ∆k) są bardzo małe, to możemy dokonać przejścia granicznego

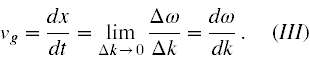
Spróbujemy zatem przyrównać, dla wygody obliczeniowej⁹, odwrotność prędkości cząstki danej wzorem (5) do wartości wynikającej ze wzoru na odwrotność prędkości grupowej pochodzącego ze wzoru (III), gdy prędkość fazowa jest dana wzorem (3). Przekształcamy najpierw (III) korzystając ze wzoru (4)

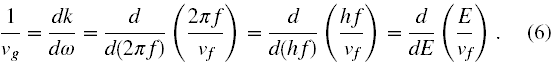
Jak wynika ze wzoru (5) odwrotność prędkości cząstki to

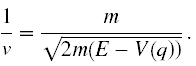
Dość łatwo można zauważyć, że

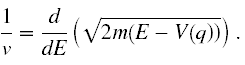
Zatem przyrównując

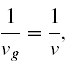
otrzymujemy

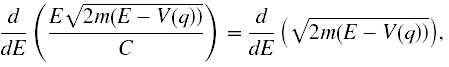
czyli

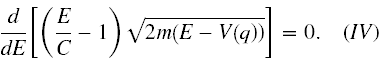
Oczywiście jasno widać, że wyrażenie w nawiasie kwadratowym w (IV) nie może zależeć od E. Ponieważ V(q) zależy tylko od współrzędnych uogólnionych, a C może być tylko funkcją E, to równanie (IV) może tylko wtedy być spełnione, gdy pierwszy czynnik wyrażenia pod pochodną jest równy zeru. Stąd

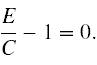
Zatem ostatecznie C = E i wzór (3) przyjmuje postać

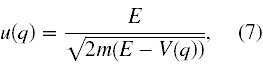
gdzie u(q), to poszukiwana przez nas postać prędkości fazowej fal de Broglie’a.

Przed przejściem do dalszych rozważań musimy sobie odpowiedzieć na pytanie, w jakich warunkach fizycznych wolno nam jeszcze stosować do fal de Broglie’a tę specyficzną wersję zasady Jacobiego, czyli optykę geometryczną dla materii? W tym celu obliczmy długość tychże fal ¹⁰ biorąc pod uwagę relacje (4) oraz (5)

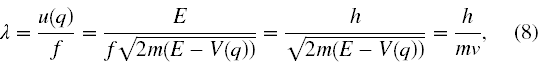
czyli jest to wartość stałej Plancka podzielonej przez wartość pędu cząstki.

Jak potwierdzają to badania doświadczalne, chociażby pierwsze, które udowodniło istnienie fal materii, czyli doświadczenie Davissona-Germera (patrz np. [8]¹¹), stosowalność optyki geometrycznej w wersji dla fal de Broglie’a, czyli zasady Jacobiego z prędkością fazową (7) kończy się, gdy istotne wymiary układu fizycznego zbliżają się do wartości długości tych fal danej wzorem (8).

I tak we wspomnianym doświadczeniu strumień elektronów miał według tego wzoru długość fali λ = 0,142 nm, która była wielkością tylko nieznacznie mniejszą od odległości między rzędami atomów w krysztale niklu, dzięki czemu był on idealną siatką dyfrakcyjną dla fal tej długości.

Opierając się na podobnych argumentach Schrödinger w swoich pracach uzasadnia, że w atomie wodoru, z uwagi na jego rozmiary, które są zbliżone do długości λ fali de Broglie’a dla elektronu nie można już stosować praw fizyki sformułowanych jako mechaniki klasyczna ¹², ale kierując się analogią ze światłem należy poszukać równania falowego ¹³ dla fal materii słusznego zarówno dla cząstek swobodnych, jak i związanych.

Jako właściwego kandydata na równanie falowe dla fal de Broglie’a Schrödinger wskazał równanie falowe, które spełniają fale podłużne ciśnienia p rozchodzące się w pewnej objętości rozciągliwego płynu zawartego w ograniczonej objętości, które ma postać

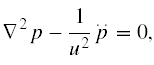
gdzie u jest stałą prędkością propagacji fal podłużnych ¹⁴, jedynych fal możliwych w przypadku płynu ¹⁵.

Jeśli chodzi o fale de Broglie’a to będzie „falować” ich funkcja falowa oznaczana jako Ψ ¹⁶ i to ona musi spełniać równanie falowe. Gdy nie uwzględniamy spinu funkcja ta jest w ogólności wielkością skalarną zespoloną. Zatem po zastąpieniu p przez Ψ i podstawieniu za u wielkości danej wzorem (7) postulowane równanie falowe dla fal materii przyjmuje postać ¹⁷

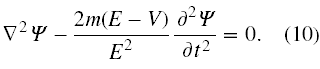
Jednak w zasadzie Jacobiego jest ograniczenie, że pole oddziaływania musi być zachowawcze i E musi być stałą ruchu. W przypadku stanów związanych w atomie wodoru oznacza to, że stan elektronu musi być stacjonarny, czyli całkowita energia elektronu musi być stała. Zatem chodzi nam o to, aby w funkcji falowej była o tym fakcie zapisana informacja. Jedyny prosty sposób na to, to przyjęcie, że w funkcji Ψ(x,y,z,t) zmienne x,y,z dadzą się odseparować od zmiennej t, czyli funkcję falową można zapisać w formie następującego iloczynu ¹⁸

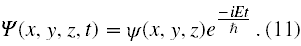
Podstawiając to do (10) otrzymujemy

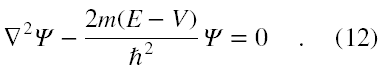
Po paru prostych przekształceniach otrzymujemy oczywiście podstawową postać stacjonarnego równania Schrödingera

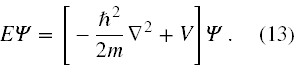
3. Wyprowadzenie równania niestacjonarnego

Aby otrzymać równanie niestacjonarne policzmy pochodną po czasie z Ψ danej wzorem (11). Stąd

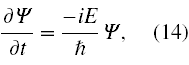
oraz dokonując przekształceń mamy

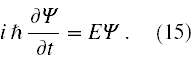
Podstawiając to za lewą stronę (13) otrzymujemy ostatecznie

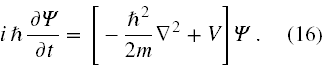
Równanie ma matematyczną własność liniowości, a to oznacza, że kombinacja liniowa ¹⁹ dowolnych jego rozwiązań jest także jego rozwiązaniem.

Należy zwrócić uwagę, że wyprowadzenie wzoru (16) nastąpiło przy założeniu, iż Ψ opisuje stan stacjonarny. A co w ogólnym przypadku, gdy rozwiązanie nie będzie stacjonarne, na przykład dla przejść kwantowych, gdy potencjał pola V(q,t) jest zależny od czasu ? Jest oczywistym, że w takiej sytuacji dokonane wyprowadzenie nie jest poprawne. Jednak tutaj Schrödinger wyraża nadzieję, że przyszłość pokaże, że równanie jest mimo to słuszne.

4. Epilog

Gdy byłem studentem fizyki i uczęszczałem na wykład Mechanika kwantowa I, znaczna część tego wykładu nie była dla mnie tajemnicą. Już trzy lata wcześniej mocno zainteresowałem się tą dziedziną fizyki. Jednak w miarę rozwoju wykładu zaczynałem dostrzegać pewne luki i niejasności w tej teorii. W końcu doszedłem do wniosku, że warto byłoby prześledzić jak powstały podstawowe równania kwantowe tj. Schrödingera i Diraca. O ile tego drugiego wyprowadzenia są dostępne w podręcznikach mechaniki kwantowej po polsku, to tego pierwszego nie ma nawet w takowych podręcznikach po angielsku.

Powyższa sytuacja wydała mi się niedobrą i postanowiłem upowszechnić głębszą wiedzę o równaniu Schrödingera. Stąd jakiś czas temu opracowałem artykuł o pierwszej metodzie wyprowadzeniu jego wersji stacjonarnej [11], o czym już wspominałem wyżej. A teraz powstała część kończąca cykl, czyli opowiadająca o drugiej metodzie prowadzącej do zarówno równania stacjonarnego, jak i niestacjonarnego

UWAGI

(¹) Rozdział II, §16 Zasada Jacobiego.

(²) Takim polem może być pole grawitacyjne lub pole elektryczne, dla którego istnieje potencjał. Jednak nie może nim być np. pole magnetyczne, czy pole elektryczne otrzymywane w wyniku zjawiska indukcji elektromagnetycznej.

(³) §1.Podstawowe prawa optyki geometrycznej.

(⁴) Faktyczne sformułowanie zasady Fermata to wzór

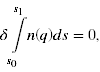
(⁵) Naszym zdaniem bezpośrednie zacytowanie tu dalszych fragmentów prac Schrödingera, z uwagi na jego intuicyjny język skierowany do zawodowych fizyków, zamiast przynieść wyjaśnienie czytelnikowi, spowodowałoby jeszcze większe zagmatwanie.

(⁶) Wówczas, teraz jeszcze dochodzi trzeci optyka kwantowa i jej odpowiednik elektrodynamika kwantowa.

(⁷) Do niedawna, także w szkole średniej, częstotliwość fali w optyce falowej oznaczało się jako ν.

(⁸) Dygresja nasza powstała w oparciu o §32 Szybkość grupowa w [5] oraz §2.1.Periodyczny ruch falowy. Prędkość fazowa i grupowa w [7].

(⁹) Tak właśnie to liczył Schrödinger.

(¹⁰) Już od kilkudziesięciu lat nie ulega wątpliwości, że dla fal de Broglie’a jedyną wielkością mierzalną bezpośrednio w doświadczeniu jest ich długość fali λ.

(¹¹) §5.5 Doświadczenie Davissona i Germera.

(¹²) Prawa mechaniki klasycznej mogą być sformułowane w formie równań Newtona, ale także w formie równań Lagrange’a II rodzaju, równań Hamiltona, równania Hamiltona-Jacobiego, zasady Maupertuis czy zasady Jacobiego itd.. Wszystkie one są sobie równoważne w pewnych granicach, a zasadnicza różnica polega na tym, że niektóre problemy fizyczne łatwiej rozwiązać przy pomocy jednego formalizmu, a drugie przy pomocy innego.

(¹³) Schrödinger argumentuje to w formie równania postaci mechanika klasyczna : mechanika falowa = optyka geometryczna : optyka falowa.

(¹⁴) Niemożliwe jest tu np. powołanie się na fale elektromagnetyczne, które spełniają takie równanie, ale są falami poprzecznymi.

(¹⁵) Przykładem fal podłużnych sprężystych, które spełniają takie równanie są np. fale dźwiękowe [9]. Na analogiczność problemu ruchu falowego cząstki w polu sił zewnętrznych i propagacji fal akustycznych w niejednorodnym gazie wskazuje Schiff [10], §6.Wyprowadzenie równania falowego. Zapotrzebowanie na równanie falowe.

(¹⁶) Powszechnie uznawaną za poprawną interpretację fizyczną tej wielkości jest interpretacja statystyczna Borna [12]. Schrödinger wskazał inną interpretację, ale nie została ona przyjęta za poprawną fizycznie [11].

(¹⁷) Współrzędne uogólnione w potencjale zastąpiliśmy „zwykłymi” współrzędnymi położeniowymi. Zakładamy, że w przestrzeni nie ma żadnych ograniczeń. Równania więzów są po prostu równaniami nie dającymi faktycznych ograniczeń.

(¹⁸) Schrödinger część zależną od czasu funkcji falowej zapisywał z plusem w wykładniku. Dzisiaj przyjmuje się, że jest to sprzężenie funkcji falowej. Ponadto nie używano jeszcze symbolu ℏ.

(¹⁹) Dla dowolnych dwóch rozwiązań (11) równania (16) Ψ₁ i Ψ₂, ich kombinacja liniowa to αΨ₁ + βΨ₂ , gdzie α i β, to dowolne liczby zespolone.

LITERATURA

[1] E. Schrödinger, Quantisierung als Eigenwertproblem I, Annalen der Physik, 79, 361 (1926).

[2] E. Schrödinger, Quantisierung als Eigenwertproblem II, Annalen der Physik, 79, 489 (1926).

[3] E. Schrödinger, Four Lectures on Wave Mechanics, Blackie & Son Limited, London and Glasgow, 1928.

[4] W. Rubinowicz, W. Królikowski, Mechanika Teoretyczna, Rozdział II, §16 Zasada Jacobiego, PWN, Warszawa 1978.

[5] Sz. Szczeniowski, Fizyka Doświadczalna, Część IV Optyka, PWN, Warszawa 1983.

[6] P. Dirac, Prof. Erwin Schrödinger, For.Mem.R.S., Nature 189, 355–356 (1961).

[7] J. Meyer-Arendt, Wstęp do optyki,PWN, Warszawa 1979.

[8] H. Enge, M. Wehr, J. Richards, Wstęp do fizyki atomowej, PWN, Warszawa 1983.

[9] W. Salejda, Ruch falowy, Politechnika Wrocławska, Instytut Fizyki, Wrocław 2007.

[10] L. Schiff, Mechanika kwantowa, PWN, Warszawa 1977.

[11] J. Szcząchor, Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 2.

[12] J. Szcząchor, Co to jest funkcja falowa i po co jej używamy?.