Rachunek różniczkowy i całkowy w fizyce szkolnej - część 3

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: czwartek, 18, maj 2015 11:42

Autor : Janusz Szcząchor

Zadanie 2.62, B.Mendel, J.Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Koło toczy się bez poślizgu po drodze z prędkością v = 2m/s. Oblicz wartość prędkości punktów A i B znajdujących się na obwodzie koła (rys. 2.19). Naszkicuj tor każdego z punktów. Zadanie rozwiąż wykorzystując rachunek różniczkowy.

Rozwiązanie

Zadanie to już zostało rozwiązane bez użycia rachunku różniczkowego, lecz ponowię jego rozwiązanie z użyciem właśnie tego narzędzia, aby pokazać jakie ono daje nowe możliwości. Będzie to także pouczające ćwiczenie pokazujące jak w praktyce wykonywać transformacje współrzędnych punktów związane z przechodzeniem z jednego do innego układu współrzędnych.

Mam nadzieję, że przeszedłeś już kurs geometrii analitycznej, bo bez niej się nie obejdzie. Co do spraw technicznych, to w poniższych wzorach czasami używam kropki, aby nie było wątpliwości, gdzie należy wykonać mnożenie.

Najpierw spróbujmy opisać analitycznie ruch dowolnego punktu D na obwodzie koła obracającego się wokół swojego środka, tutaj zgodnie z kierunkiem ruchu wskazówek zegara (patrz rysunek nr 1 - jest to tylko szkic, a nie wierne odzwierciedlenie rzeczywistości (!)).

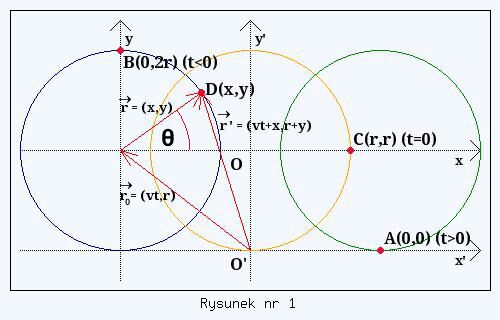
Chwilowe położenie punktu D w układzie współrzędnych (x,y) jest dane poprzez następujące wartości współrzędnych

x = r·cosθ , (1a)

y = r·sinθ . (1b)

Skoro koło ma się obracać ze stałą prędkością kątową o odpowiedniej wartości (ustaliliśmy, że wynika to z warunku, aby koło poruszało się ze stałą prędkością v tocząc się bez poślizgu, czyli 2πr = vT, patrz W jaki sposób nauczyć się rozwiązywać zadania z fizyki - część 15) oraz, że obrót koła jest zgodny z ruchem wskazówek zegara (co oznacza, że kąt θ przebiega wartości coraz bardziej ujemne) musimy przyjąć, że θ = - φt, gdzie φ - to stała wartość dodatnia. Wtedy wzory (1a) i (1b) przyjmują postać

x = r·cos(-θt) , (2a)

y = r·sin(-θt) . (2b)

Wprowadźmy teraz nowy układ współrzędnych oznaczony na rysunku nr 1 jako primowany, względem którego (nie patrząc na obrót koła) nasze koło (koloru niebieskiego) będzie się poruszać ruchem jednostajnym prostoliniowym z prędkością v. Wtedy współrzędne środka koła w tym nowym układzie współrzędnych to

x₀ = vt , (3a)

y₀ = r . (3b)

Składając następnie ruch postępowy koła z jego ruchem obrotowym otrzymamy, przy dalszym założeniu, że koło toczy się z prędkością v bez poślizgu, nowe współrzędne punktu D na obwodzie tego koła w nowym układzie primowanym współrzędnych.

Z rysunku nr 1 widać, że położenie punktu D w układzie (x,y) jest dane poprzez wektor r, a w układzie (x',y') poprzez wektor r'. Aby otrzymać wartości współrzędnych wektora r' trzeba dodać współrzędne wektorów zgodnie ze wzorem

r' = r + r₀ , (4)

gdzie r₀ = (vt,r). Prowadzi to do wniosku, że położenie punktu D w układzie primowanym jest teraz dane wartościami (wektor r₀ nie jest wektorem stałym, na rysunku nr 1 jest on wrysowany dla pewnej chwili czasu t, patrz równania (3a) i (3b))

x' = vt + r·cos(-φt) , (5a)

y' = r + r·sin(-φt) . (5b)

Skoro warunek toczenia się koła bez poślizgu oznacza, że okres obrotu koła to T=2πr/v, więc możemy obliczyć prędkość kątową z jaką toczy się koło, tj.

φ = 2π/T = 2π/(2πr/v) = v/r . (6)

Zatem ostatecznie równania ruchu punktu D w układzie primowanym przyjmują postać

x' = vt + r·cos(-vt/r) , (7a)

y' = r + r·sin(-vt/r) . (7b)

Po otrzymaniu równań ruchu dowolnego punktu na obwodzie toczącego się koła w układzie primowanym przejdźmy do analizy ruchu szczególnego punktu. Oznaczmy ten punkt jako C.

Dla wygody teraz przyjmiemy, że ruch koła zaczyna się dla pewnej ujemnej wartości czasu, przechodzi przez wartość 0 i kontynuuje dla czasu dodatniego. Założymy, że położenie punktu C w dowolnej chwili czasu t będzie opisane równaniami (7a) i (7b). Aby zobaczyć gdzie punkt C znajdował się w chwili t = 0 wstawmy tę wartość do tych równań i otrzymujemy, że

x'(t=0) = r, (8a)

y'(t=0) = r. (8b)

Punkt C w tym położeniu jest zaznaczony na rysunku nr 1.

Policzmy teraz w jakiej chwili czasu punkt C będzie się znajdował w położeniu A, a w jakiej w położeniu B. Wystarczy wziąć pod uwagę wartość współrzędnej y' punktu C, ponieważ w ruchu po okręgu nie ma innych położeń, które posiadałaby te same wartości współrzędnych y' (w okresie jednego obrotu koła) co punkty A i B.

1) Dla punktu A rozwiązujemy równanie

0 = r + r sin(-vt/r),

sin(-vt/r) = -1,

-vt/r = -π/2,

t = (πr)/2v. (9)

2) Dla punktu B rozwiązujemy równanie

2r = r + r sin(-vt/r),

sin(-vt/r) = +1,

-vt/r = π/2,

t = -(πr)/2v. (10)

Skoro znamy równania ruchu naszego punktu materialnego dane wzorami (7a) i (7b), więc możemy obliczyć składowe jego wektora prędkości. Obliczenia wykonujemy zgodnie z poniższymi rachunkami obliczając pochodne po czasie współrzędnych x' i y'.

dx'(t)/dt = v + r·(-1)·(-v/r)·sin(-vt/r) = v + v·sin(-vt/r), (11a)

dy'(t)/dt = r·(-v/r)·cos(-vt/r) = -v·cos(-vt/r). (11b)

Możemy teraz już policzyć składowe wektora prędkości v' punktu C w chwilach czasu odpowiadających położeniom A i B wstawiając do wzorów (11a) i (11b) odpowiednie wartości czasu. Otrzymujemy

1) dla punktu A,

v'_x(t = (πr)/2v) = dx'(t = (πr)/2v)/dt = v + v·sin(-π/2) = 0 , (12a)

v'_y(t = (πr)/2v) = dy'(t = (πr)/2v)/dt = -v·cos(-π/2) = 0 . (12b)

2) Dla punktu B,

v'_x(t = -(πr)/2v) = dx'(t = -(πr)/2v)/dt = v + v·sin(π/2) = 2v , (13a)

v'_y(t = -(πr)/2v) = dy'(t = -(πr)/2v)/dt = -v·cos(π/2) = 0 . (13b)

Zatem w punkcie A prędkość punktu C jest równa 0 m/s, natomiast w punkcie B jest równa 2v i jest skierowana poziomo w prawo. Jest istotnie dwa razy większa niż dla środka koła.

Otrzymaliśmy wyniki identyczne jak dla obliczeń bez użycia rachunku różniczkowego, ale teraz potrafimy podać wartości współrzędnych wektora prędkości punktu C w dowolnym punkcie jego toru ruchu, a także potrafimy zrobić to samo dla jego przyspieszenia, co bez użycia rachunku różniczkowego i geometrii analitycznej byłoby praktycznie niewykonalne. I to jest wielka zaleta tych matematycznych narzędzi.