W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 27
- Szczegóły
- Kategoria: Zadania z fizyki
- Opublikowano:środa, 7 listopad 2018 11:31
- Autor : Janusz Szcząchor
- O mnie:
- Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu
Zadanie nr 5.67 , H. Kaczorek, Z. Słówko - "Zbiór zadań z fizyki",WSiP,Warszawa 1981
Oblicz opór zastępczy obwodu przedstawionego na rysunku 67. » Rozwiązanie
Zadanie nr 5.72 , H. Kaczorek, Z. Słówko - "Zbiór zadań z fizyki",WSiP,Warszawa 1981
Woltomierz, którego zakres skali wynosi 5V, ma opór wewnętrzny 200Ω. Oblicz wartość dodatkowego oporu, jaki należy włączyć do woltomierza, aby możliwe były pomiary napięcia do 100V. » Rozwiązanie
Zadanie nr 5.73 , H. Kaczorek, Z. Słówko - "Zbiór zadań z fizyki",WSiP,Warszawa 1981
Jedna działka mikroamperomierza odpowiada 10µA. Cała skala przyrządu zawiera 100 działek. Opór wewnętrzny mikroamperomierza wynosi 100Ω. W jaki sposób z przyrządu tego zrobić amperomierz, za pomocą którego można będzie mierzyć natężenia prądu aż do 1 A? » Rozwiązanie
Zadanie nr 17.56 , M.S.Cedrik i inni - "Zadania z fizyki", PWN, Białystok 1975
Znaleźć natężenie prądu w każdej części obwodu (rys.70), jeżeli E1 = 24 V, E2 = 18 V, R1 = 20 Ω, R2 = R3 = 2 Ω. Opory wewnętrzne źródeł zaniedbać. » Rozwiązanie
Wstęp
Przedmiotem tej części Naszego cyklu są prawa Kirchhoffa, które tutaj przypomnimy w następującej formie, zaczerpniętej z [1].
- 1)
- W dowolnym węźle obwodu elektrycznego składającego się z wielu oczek suma prądów musi być równa zeru.
- 2)
- Suma zmian potencjału napotykanych przy dokonywamiu obiegu wokół dowolnego zamkniętego obwodu elektrycznego (oczka) jest równa zeru.
- Gdy "przechodzimy" przez opór w kierunku zgodnym z kierunkiem płynięcia prądu, wówczas zmiana potencjału wynosi - IR; gdy opór jest "przebywany" w kierunku przeciwnym, zmiana ty wynosi + IR.
- Gdy źródło SEM jest "przebywane" w kierunku SEM, zmiana potencjału jest równa + E; gdy obrany jest kierunek przeciwny, wówczas zmiana ta wynosi - E.
Z powyższych praw można wyprowadzić reguły łączenia szeregowego i równoległego oporów.
§1 Rozwiązanie zadania nr 5.67 1
Obwód elektryczny, o którym mowa w zadaniu ma następującą postać.
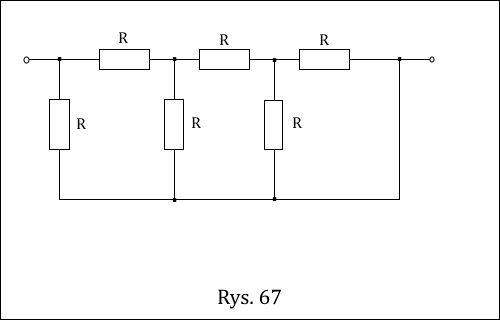
Wbrew wyglądowi powyższego rysunku można dla tego obwodu obliczyć opór zastępczy korzystając tylko ze wzorów na łączenie równoległe i szeregowe oporników, które tutaj mają identyczną wartość oporu daną zmienną R. Wystarczy tylko umiejętnie przerysować obwód do bardziej przystępnej postaci przedstawionej poniżej (Rys. nr 1).
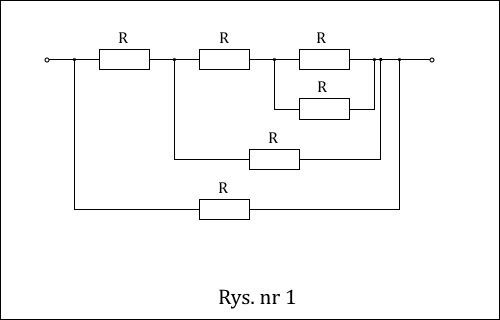
Po dokonaniu niezbędnych obliczeń nie powinno ulegać wątpliwości, że opór zastępczy takiego układu to 8/13 R.
§2 Rozwiązanie zadania nr 5.72 2
Pierwsze zagadnienie, które należy rozstrzygnąć, to pytanie jak należy włączyć dodatkowy opór do woltomierza, czy równolegle, czy też szeregowo? W tym celu musimy wyjaśnić w jakim celu włączamy taki opornik do woltomierza.
Woltomierz, to urządzenie, które ma zmierzyć panujące napięcie w jakiejś części obwodu elektrycznego. Z natury rzeczy taki woltomierz musi pobierać jakiś prąd z badanego obwodu, ale nie może on być zbyt duży, aby nie zaburzać prawidłowego działania takiego obwodu i dlatego woltomierze muszą mieć bardzo duży opór. Dołączenie jakiegokolwiek oporu równolegle spowoduje zmniejszenie oporu, a tym samym wzrost płynącego prądu przez układ woltomierza, co dyskwalifikuje ten sposób dołączenia.
Spójrzmy teraz z drugiej strony. Gdy dołączamy jakikolwiek opornik równolegle do woltomierza, to nadal na nim panuje całe napięcie. Aby ten woltomierz mógł prawidłowo działać napięcie na nim nigdy nie może przekroczyć 5V. Tylko dołączając opornik szeregowo spowodujemy podział napięcia między dodatkowy opornik, a woltomierz. Tym samym należy rozważyć następujący układ elektryczny, patrz poniższy rysunek nr 2 (woltomierz został podzielony schematycznie na miernik o zerowym oporze oraz opornik reprezentujący jego opór wewnętrzny).
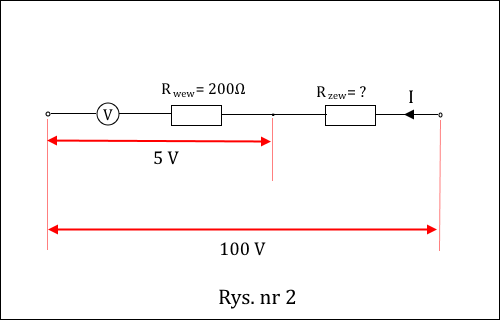
W ten sposób, gdy na woltomierzu i zewnętrznym oporniku sumaryczny spadek napięcia będzie 100V, to na samym woltomierzu tylko 5V.
Korzystając z tego, że przez oba oporniki, jak i woltomierz płynie ten sam prąd, oznaczając 5V jako Uwew, a 100V jako Uzew oraz oznaczając opory tak jak na Rys. nr 2 możemy ułożyć następującą proporcję
I = I , (1)
Uwew / Rwew = Uzew / [Rwew + Rzew] . (2)
Rozwiązując równanie (2) otrzymujemy wynik
Rzew = Rwew [Uzew - Uwew] / Uwew = 3,8 kΩ . (3)
Pozostaje tylko zmienić opis skali na woltomierzu.
§3 Rozwiązanie zadania nr 5.73 3
Nie powinno ulegać wątpliwości, że na tym etapie nauki fizyki może wchodzić w grę jedynie dołączenie dodatkowego oporu, szeregowo lub równolegle do mikroamperomierza. Aby wybrać właściwe rozwiązanie musimy zastanowić się nad sposobem włączenia tego przyrządu do obwodu elektrycznego.
Skoro amperomierz ma mierzyć natężenie prądu płynącego przez jakieś urządzenie elektryczne, to musi on być połączony szeregowo z tym urządzeniem. Połączenie dodatkowego opornika szeregowo z mikroamperomierzem zwiększa opór sumaryczny tego przyrządu, a w konsekwencji i urządzenia. Opór amperomierza nie może być zbyt duży, aby nie ograniczać prądu płynącego przez urządzenie, a tym samym zaburzać jego prawidłowej pracy.
Stąd widać, że w grę powinno wchodzić jedynie podłączenie jakiegoś opornika równolegle do mikroamperomierza. Zastanówmy się, czy tak jest faktycznie?
Mikroamperomierz ma 100 działek na skali, oznaczmy tę liczbę jako n. Jedna działka oznacza prąd o natężeniu 10µA, co oznaczymy jako I. Zatem maksymalny prąd, który może płynąć przez miernik to
nI = 1mA . (1)
Prąd o większym natężeniu może uszkodzić miernik, a z pewnością nie da się go nim zmierzyć.
Jedynym sposobem jest dołączenie równolegle do mikroamperomierza tak dobranego opornika, że gdy przez mikroamperomierz płynie prąd o natężeniu 1mA, to przez ten opornik płynie prąd o takim natężeniu, że przez niego i mikroamperomierz płynie sumaryczny prąd o natężeniu 1A, który oznaczymy jako I1. Stąd należy rozważyć układ elektryczny przedstawiony na Rys. nr 3.
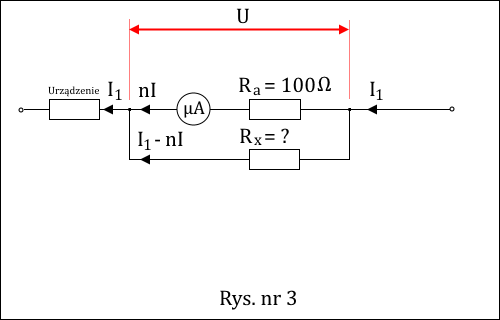
Tutaj ponownie rozdzieliliśmy mikroamperomierz na miernik o zerowym oporze i opór wewnętrzny. Napięcie panujące na mikroamperomierzu i dodatkowym oporniku musi być to samo, zatem
U = U , (2)
nIRa = (I1 - nI)Rx . (3)
Stąd wynikiem jest
Rx = nIRa /(I1 - nI) ≈ 0.1 Ω . (4)
§4 Rozwiązanie zadania nr 17.56 4
Budowa obwodu elektrycznego jest przedstawiona poniżej, na Rys. 70.
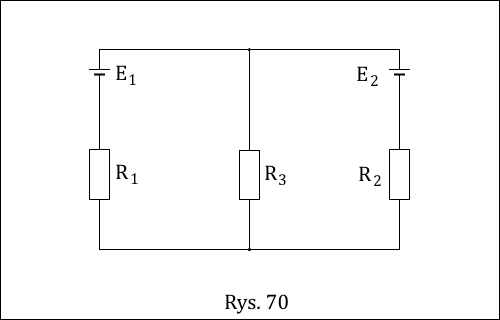
Jak widzimy, obwód elektryczny składa się tutaj z dwóch oczek, z których każde posiada źródło SEM. Na początek musimy zaznaczyć zwroty SEM za pomocą strzałek, których ostrza wskazują wyższy potencjał, czyli miejsce od którego płynie prąd elektryczny (czyli ładunki dodatnie) na zewnątrz źródła. W tym układzie "plusy" obu źródeł są ze sobą złączone tworząc jeden wspólny wyższy potencjał. Ponadto trzeba zaproponować rozkład prądów w poszczególnych gałęziach obwodu, czyli ich oznaczenia symboliczne oraz zwrot, w którym one płyną. Wszystko to przedstawia Rys. nr 4.
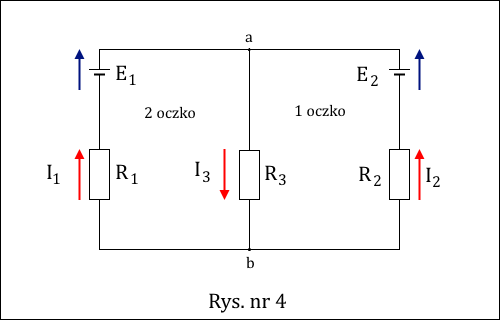
Teraz możemy wykorzystać II prawo Kirchoffa do napisania bilansu napięć w obu małych oczkach sieci. Przyjmujemy, że w obu oczkach kierunek obiegu jest zgodny z ruchem wskazówek zegara. W oczku nr 1 otrzymujemy następujące równanie
- E2 + I2R2 + I3R3 = 0 , (1)
a w oczku nr 2
- I3R3 - I1R1 + E1 = 0 . (2)
Ponadto dla węzła "b" (podobnie jak dla węzła "a") możemy napisać wynikający z I prawa Kirchhoffa bilans prądów
I3 = I1 + I2 . (3)
Rozwiązywanie układu (1-3) zaczniemy od wstawienia równania (3) do (1) i (2). Otrzymamy wtedy układ 2 równań z dwiema niewiadomymi. Zostaną one zapisane w specjalnie uporządkowany sposób.
(R1 + R3)I1 + R3I2 = E1 . (4)
R3I1 + (R2 + R3)I2 = E2 . (5)
Z uwagi na fakt, że ogólnie n-oczkowy obwód elektryczny prowadzi do układu n równań liniowych z n niewiadomymi, który to układ jest zbyt skomplikowany, aby go rozwiązywać metodą podstawień układ (4-5) rozwiążemy przy pomocy wzorów Cramera. Czasami tą metodę nazywa się metodą wyznaczników. Jej opis na poziomie elementarnym, czyli układu 2 równań z 2 niewiadomymi można znaleźć w [2], a dla przypadku ogólnego np. w [3].
Rozwiązywanie układu (4-5) należy rozpocząć od zbadania, czy układ ten jest układem Cramera. W tym celu musimy wypisać macierz główną układu (4-5), która ma postać
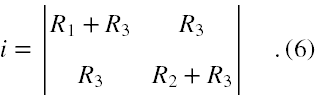
Wyznacznik tej macierzy jest równy (1)
Wi = (R1 + R3)(R2 + R3) - R32 = R1R2 + R1R3 + R2R3 . (7)
Jak widać z (7) jest on zawsze większy od zera, a zatem układ (4-5) jest układem Cramera i ma dokładnie jedno rozwiązanie.
W celu uzyskania rozwiązania układu (4-5) musimy wypisać jeszcze dwie następujące macierze, które powstają z zastąpienia w (6) pierwszej lub drugiej kolumny kolumną napięć. Dla uzyskania wartości natężenia prądu I1 tworzymy macierz i1 postaci
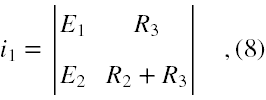
a dla uzyskania wartości natężenia prądu I2 tworzymy macierz i2 w formie
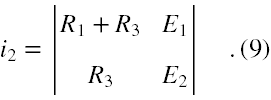
Rozwiązania, czyli wartości natężenia prądu są dane wzorem
Ik = Wk/Wi, k = 1,2 , (10)
gdzie Wk, to wyznacznik macierzy i1 lub i2. Wi to wyznacznik dany wzorem (7).
Ostatecznie natężenia są dane jako
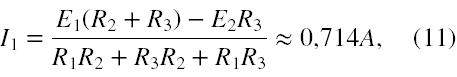
oraz
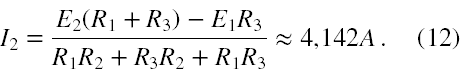
Na podstawie (3) otrzymujemy, że I3 jest równe
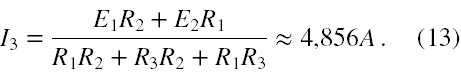
(1) Wyznacznik każdej macierzy o wymiarach 2x2 postaci
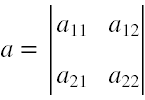
jest równy Wa = a11a22 - a21a12.
LITERATURA
[1] D. Halliday, R. Resnick, Fizyka tom II, rozdział 32, PWN, Warszawa 1972.
[2] W. Leksiński, B. Macukow, W. Żakowski Matematyka w zadaniach, część 1, rozdział 2, WNT, Warszawa 1972.
[3] A. Mostowski, M. Stark, Elementy algebry wyższej, rozdział IV, PWN, Warszawa 1977.
