W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 16

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: wtorek, 18 sierpień 2015 14:20

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 2.77, Bogdan Mendel, Janusz Mendel - Zbiór zadań z fizyki,WSiP,Warszawa 1976

Z jakim przyspieszeniem a powinna się poruszać równia pochyła o kącie nachylenia α = π/6, aby ciężarek umieszczony na równi przebył w czasie Δt = 5 s drogę l = 20 cm pod górę równi (rys. 2.29)? Opory ruchu zaniedbać.

Rozwiązanie

Zadanie to można rozwiązać używając pojęcia siły bezwładności, o czym świadczy choćby umieszczenie tego zadania w paragrafie 2.6. Siły bezwładności. Szczęśliwie się składa, że na początku tego paragrafu podano rozwiązanie przykładowego zadania, w moim przekonaniu dobrze ilustrującego jak stosować w praktyce to pojęcie.

Jednak siła bezwładności, to wielkość fizyczna pozorna. Z drugiej strony sposoby wyjaśnienia tego zagadnienia serwowane w programie szkolnym były zawsze dla mnie niezadowalające. Wprowadza się je na tak prostym przykładzie, który ma się nijak do typowych problemów, takich jak to zadanie, gdzie zastosowanie siły bezwładności nosi cechy czarnej skrzynki.

W moim przekonaniu o wiele ciekawsze i bardziej pouczające jest rozwiązanie tego zadania bez pojęcia siły bezwładności. Jeśli interesuje Cię jakie zjawiska fizyczne kryją się faktycznie, w takim zadaniu jak to, za pojęciem tej siły, to niniejsze rozwiązanie jest właśnie dla Ciebie.

Ktoś może spytać - a dlaczego takie rozwiązanie jest bardziej pouczające?

Odpowiedzi na to pytanie tak łatwo nie uzyskasz w szkole średniej. Dopiero ucząc się podstaw relatywistyki zetkniesz się z zagadnieniem opisu praw fizyki w różnych układach odniesienia, a które to zagadnienie jest jednym z najtrudniejszych w fizyce. Dlatego warto poznać je bardziej dogłębnie już teraz.

To rozwiązanie pozwoli Ci nabrać pewnego doświadczenia w patrzeniu na zjawiska fizyczne z różnych układów odniesienia. Z mojego doświadczenia wiem, że najpierw przyzwyczaja się młodych ludzi stosować prawa fizyki w spoczywającym układzie odniesienia, a potem "szokuje" się ich takimi zjawiskami jak 'paradoks bliźniąt'. W prawach fizyki nie ma paradoksów, a jest tylko trudność, gdy nie ma się odpowiedniego doświadczenia, w ich intuicyjnym stosowaniu.

Przechodząc do meritum zakładam, że znasz już sposób rozwiązania zadania nr 2.27 ze zbioru "Mendla" (rozwiązanie nr 2 w moim poradniku) zastosowany do klocka zsuwającego się po ruchomej równi pochyłej.

Celem przypomnienia załóżmy, że początkowo równia się jeszcze nie porusza (patrz rysunek nr 1). Wtedy klocek zsuwa się po równi dzięki temu, że siła F_s nie jest zrównoważona (pogrubione litery oznaczają wektory). Natomiast siła F_n jest zrównoważona przez siłę reakcji równi siła F_r. Klocek wprawdzie też działa siłą F_n = - F_r na równię, ale gdy równia jest unieruchomiona nie ma to wpływu na sytuację fizyczną.

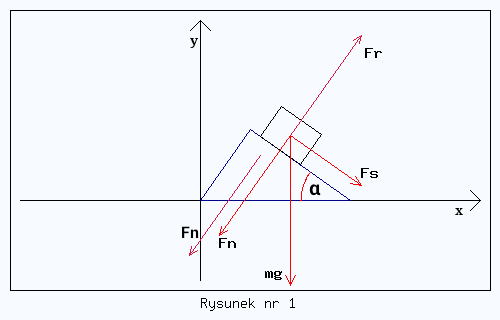
Załóżmy teraz, że równia porusza się z przyspieszeniem a o zwrocie jak na rysunku nr 2. Czy potrafisz teraz łatwo sobie wyobrazić jak równia oddziaływuje na klocek i co się z nim dzieje?

Z samej treści zadania wynika, że przy pewnej wartości przyspieszenia równi klocek powinien zacząć wznosić się w górę. Ale dlaczego?

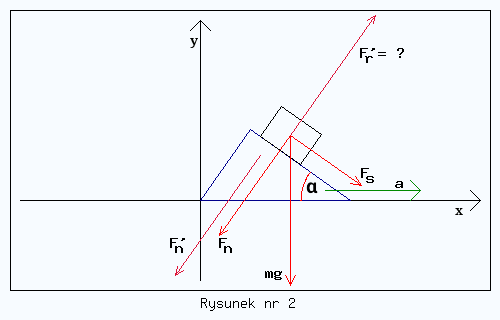
Po prostu równia zaczyna pchać klocek (ale tylko wtedy, gdy porusza się ruchem przyspieszonym, a nie jednostajnym) i to siłą F'_r (prim dla odróżnienia), której wartość wzrasta i przewyższa F_n. Powstaje wypadkowa siła większa od zera, która dodaje się wektorowo do F_s i modyfikuje ruch klocka. Na równię wprawdzie teraz działa siła F'_n o wartości identycznej, ale przeciwnym zwrocie do siły F'_r, lecz tu się domyślnie zakłada, że źródło napędzające równię jest w stanie zrekompensować tę siłę.

Takie chwyty musisz zgadnąć, samemu 'wykoncypować', bo je trudno znaleźć w książkach! Żeby lepiej zrozumieć sytuację najpierw obliczmy z jakim przyspieszeniem powinna poruszać się równia, aby klocek przestał się zsuwać?

W tym celu przede wszytkim musimy sobie odpowiedzieć na pytanie: co to znaczy, że klocek nie zsuwa się po równi?

1. W układzie związanym z równią oznacza to, że względem równi klocek ma przyspieszenie równe 0 m/s², jak również prędkość początkowa klocka jest równa 0 m/s względem niej.
2. Dla obserwatora z zewnątrz, związanego ze stołem, po którym porusza się równia klocek porusza się z takim samym przyspieszeniem, co i równia, podobnie i ich prędkości muszą być identyczne.

Kiedy tak będzie?

W przypadku układu związanego ze stołem oczywiście, gdy siła F'_r - F_n na tyle wzrośnie, że po złożeniu wektorowo z F_s obie nadadzą klockowi przyspieszenie co do wartości, jak i kierunku identyczne z przyspieszeniem równi (patrz rysunek nr 3 - rysunek jest tylko szkicem!).

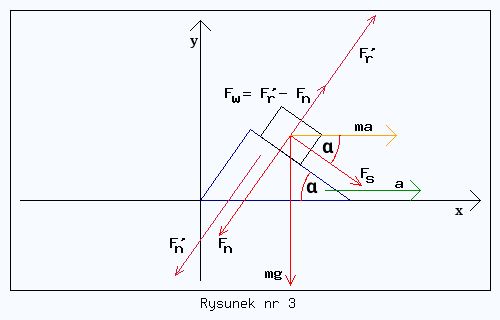
Zapisując to wektorowo mamy dla przypadku układu związanego ze stołem (tutaj pobrubieniem zaznaczono wektory)

F'_r - F_n + F_s = ma. (1)

Dzięki temu, że przyspieszenie klocka ma ten sam kierunek co przyspieszenie równi, siły F_w, F_s i ma tworzą ramiona trójkąta prostokątnego przystającego do samej równi, a zatem z tym samym kątem α. Dzięki temu, celem obliczenia przyspieszenia a wcale nie musimy znać wartości F'_r ! Zauważmy, że

cosα = F_s / ma,

czyli

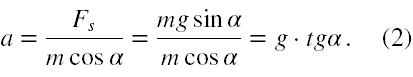
Po rozwiązaniu pomocniczego problemu przejdźmy do właściwego zagadnienia. Aby klocek zaczął poruszać się w górę równi przyspieszenie samej równi musi dalej wzrastać. Skoro powiedziano w zadaniu, że klocek ma pokonać w ciągu czasu Δt drogę l w górę równi to oznacza, że musi on mieć przyspieszenie względem samej równi o wartości

a_l = 2l/(Δt)²,

co wynika ze wzoru na drogę w ruchu prostoliniowym jednostajnie przyspieszonym.

Oznacza to dalej, że siła F_w po złożeniu wektorowo z siłą F_s nada klockowi takie przyspieszenie a_x, że po odjęciu od niego wektorowo przyspieszenia równi a otrzymamy wektor przyspieszenia o długości a_l (patrz rysunek nr 4 - jest to tylko szkic!), który jest równoległy do stoku równi (tutaj pogrubieniem oznaczono wektory)

a_x + ( - a) = a_l, (3)

gdzie

a_x = (F_w + F_s)/m. (4)

(Wzór 3 to przepis na przejście z układu związanego ze stołem do układu związanego z równią!)

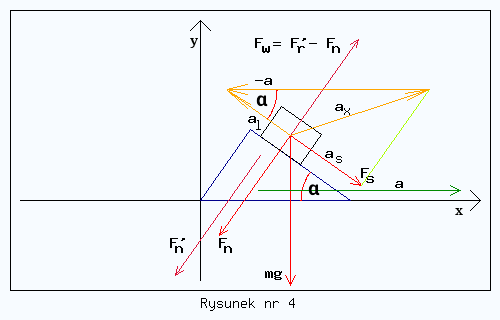
Jak tu obliczyć - a? Przyspieszenia - a, a_l i a_x nie tworzą trójkąta prostokątnego. Przyspieszenie a_x, to przyspieszenie z jakim klocek faktycznie porusza się względem stołu. Zauważmy, że z a_x można wydzielić składową a_s, jaką klockowi nadaje sama siła F_s. Teraz przyspieszenia - a, a_l i a_s tworzą dwa ramiona trójkąta prostokątnego. Zatem (pisząc skalarnie, czyli bez wektorów)

cos α = (a_l + a_s)/a,

czyli

a = (a_l + a_s)/cos α .

Wartość liczbową a_l już znamy, zatem

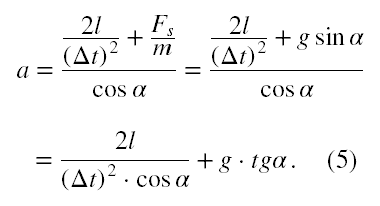
Jak widać ponownie, do uzyskania rozwiązania nie jest konieczna znajomość wartości samej siły F'_r.

Jeśli chodzi o rozwiązanie tego zadania z użyciem pojęcia siły bezwładności, to oznacza to, że teraz analizujemy sytuację tylko w układzie poruszającej się równi z przyspieszeniem a (można tu wykorzystać rysunek nr 4). Taka równia, to układ nieinercjalny i dlatego przyjmujemy, że na klocek znajdujący się na równi oprócz siły F_s działa także siła bezwładności - ma, która ma powodować jego ruch w górę równi z przyspieszeniem a_l.

Teraz zwróć uwagę, że siła F_s nadaje klockowi przyspieszenie a_s, tak jak w poprzednim rozwiązaniu. Stąd siłę bezwładności - ma należy rozłożyć na składowe równoległą i prostopadłą do stoku równi (w tym celu użyj boków samej równi). Otrzymujemy, że (po skróceniu mas, rachunki poniższe są skalarne)

cos α = a_ǁ/a, (6)

oraz

sin α = a_⊥/a. (7)

Klocek porusza się z przyspieszeniem a_ǀ, bo

a_ǀ = a_ǁ - a_s,

czyli mamy

a_∥ = a_l + a_s.

Dzięki (6) mamy, że

a cosα = a_l + a_s,

co wobec określenia a_s (które powinieneś znać z lekcji fizyki) i wzorowi na a_l już bezpośrednio prowadzi do wzoru (5).

Na podstawie przedstawionych przeze mnie obu rozwiązań powinieneś się przekonać, że siła bezwładności jest faktycznie siłą pozorną. To tylko siła F'_r powoduje ruch klocka w górę równi. Jednak dzięki temu, że znajomość tej siły nie jest konieczna do obliczenia przyspieszenia klocka, jest możliwe posługiwanie się pojęciem siły bezwładności.