Rachunek różniczkowy i całkowy w fizyce szkolnej - część 2
- Szczegóły
- Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej
- Opublikowano: sobota, 16, styczeń 2016 10:43
- Autor : Janusz Szcząchor
zadanie nr 1.25, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976
Prędkość prądu rzeki o szerokości d = 600 m wynosi v1 = 2 m/s. Pływak może płynąć z największą prędkością v2 = 6km/h. a) Jaki największy kąt może tworzyć z linią brzegu wypadkowa prędkość pływaka? b) W którym miejscu i po jakim czasie znajdzie się pływak w tym przypadku na przeciwległym brzegu rzeki? Rozwiąż zadanie przy pomocy rachunku różniczkowego.
Rozwiązanie
Zadanie zostało już rozwiązane metodą geometryczną w W jaki sposób nauczyć się rozwiązywać zadania z fizyki?- Część 5. Lecz jeżeli chcesz studiować fizykę lub coś pokrewnego i znasz już rachunek różniczkowy, to może zainteresuje Cię metoda algebraiczna rozwiązania tego zadania.
Jeszcze raz naszkicujmy układ wektorów prędkości i to bez sugerowania, że kąt γ jest kątem prostym (rysunek nr 1 ).
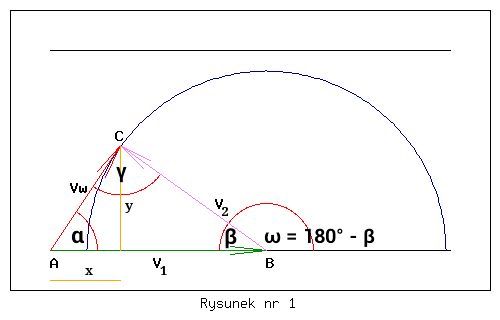
Powstaje oczywiste pytanie jak obliczyć wartość największą kąta α w sposób czysto algebraiczny ?
Zauważmy, że skoro możemy zmieniać kąt pod jakim wektor prędkości pływaka jest skierowany względem prędkości rzeki (tu oznaczony jako kąt ω), w granicach od 0° do 180°, to możemy go przyjąć jako zmienną niezależną. Wtedy kąt α, kąt jaki tworzy wypadkowa prędkości pływaka i prędkości rzeki z brzegiem rzeki jest funkcją kąta ω.
Moglibyśmy wtedy spróbować zastosować metodę szukania ekstremum kąta α jako funkcji kąta ω znaną z rachunku różniczkowego (przyrównanie pierwszej pochodnej α względem ω do zera).
Zatem stosując oznaczenia z rysunku 1 mamy
tg α = y/x .
Tutaj osobom nieobytym z takimi metodami postępowania śpieszę wyjaśnić, że y i x traktujemy po prostu jako pomocnicze wektory o wymiarze prędkości.
Dalej wyrażamy y i x jako funkcje prędkości V1 , V2 i jakiejś funkcji kąta β, czyli
sinβ = y/V2,
a stąd
y = V2 sinβ.
I dalej
(V1 - x)/V2 = cos β,
V1 - x = V2 cos β,
x = V1 - V2 cos β.
Zatem
tg α = ( V2 sinβ )/( V1 - V2 cosβ ).
Należy jeszcze funkcje kąta β wyrazić jako funkcje kąta ω. Skoro
β = 180°- ω, (1)
to stosując wzory redukcyjne mamy
sinβ = sin(180° - ω) = sinω, (2a)
cosβ = cos(180° - ω) = - cosω. (2b)
Zatem
tgα = ( V2 sinω )/( V1 + V2 cosω ), (3)
oraz w końcu mamy
α = arc tg [ ( V2 sinω )/( V1 + V2 cosω ) ]. (4)
Kąt α, jak widać, wyraża się jako funkcja złożona kąta ω. Niemniej spróbujemy sobie poradzić z rachunkami. Przypomnijmy, że warunkiem koniecznym na to, aby funkcja miała ekstremum w jakimś punkcie x0 należącym do jej dziedziny jest, aby jej pochodna w tym punkcie istniała i była równa 0.
Wydaje się, że kąt α jako funkcja ω powinien być funkcją ciągłą, bo tangens istnieje w przedziale [0,π/2), czyli o ile α jest mniejsze od π/2. Pozostałe funkcje wewnętrzne nie mają tych problemów. Nie będziemy jednak tu szczegółowo badać przebiegu tej funkcji, bo to i tak będzie prowadzić przez potrzebne nam rachunki.
Skorzystamy z tego, że jeżeli uda nam się policzyć dα/dω i znajdziemy rozsądną wartość ω, dla której dα/dω = 0, to będzie oznaczać, że rachunki prowadziliśmy prawidłowo i nie naruszyliśmy założeń twierdzenia. Zatem obliczamy pochodną α względem ω korzystając wielokrotnie z reguły obliczania pochodnej funkcji złożonej oraz pochodnej ułamka funkcyjnego i mamy
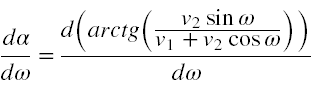
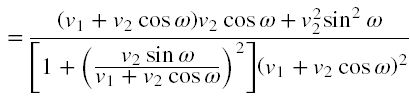
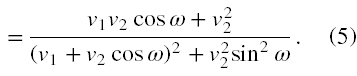
Jak widać dα/dω istnieje. Przyrównajmy ją do 0, czyli faktycznie przyrównujemy licznik do zera i zakładamy, że dla wartości zmiennej ω zerującej licznik, mianownik nie będzie równy 0. Zatem
V1 V2 cosω + (V2)2 = 0 ,
czyli
cosω = - V2 /V1 . (6)
Teraz musimy wrócić do wzoru (3) na tgα i pozbyć się z niego funkcji trygonometrycznych . Ze wzorów (2b) oraz (6) mamy, że
cosβ = V2 /V1 .
Ponadto ze wzoru (2a), tożsamości sin2ω + cos2ω = 1 oraz wzoru (6) wynika, że
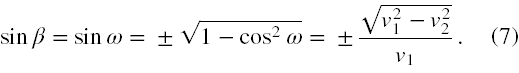
Wstawiając do wyrażenia na tgα (wzór 3) obliczony sinω (wzór 7) oraz cosω (wzór 6) otrzymujemy
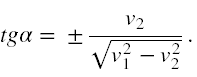
Ponieważ tgα w przedziale [0,π/2) jest dodatni, więc wybieramy znak '+'. Obliczmy teraz kwadrat Vwypadkowa (w oparciu o rysunek nr 1). Po obliczeniach jest dany on wyrażeniem
![]()
Patrząc na rysunek nr 1 widzimy, że jest to faktycznie twierdzenie Pitagorasa w trójkącie ABC, a zatem jest on istotnie trójkątem prostokątnym.
![]()
Jeżeli chcemy te obliczenia porównać z wynikiem rozwiązania geometrycznego, to wiedząc już, że jest to trójkąt prostokątny wystarczy zgodnie z rysunkiem nr 1 sprawdzić, iż w tym trójkącie z definicji sinα jest równy tyle samo, co w geometrycznym rozwiązaniu.
Pewne obliczenia powyżej pominąłem zakładając, że skoro jesteś w stanie śledzić obliczanie pochodnej, to te rachunki jako ćwiczenie też przeprowadzisz sam. W każdym razie wiesz co masz otrzymać jako wynik!
Podsumowanie
Muszę tu wyjaśnić, że najpierw znalazłem rozwiązanie tego zadania metodą właśnie opisaną powyżej, już jako absolwent uniwersytetu i nauczyciel z pewnym doświadczeniem zawodowym. Rozwiązanie geometryczne znałem ze szkoły, ale nie rozumiałem w ogóle dlaczego trójkąt wektorów prędkości jest prostokątnym.
Podane wyjaśnienie tego faktu wykorzystane w metodzie geometrycznej w części pierwszej mojego poradnika pochodzi ode mnie, jest całkowicie moim dziełem.
Przeglądając wydanie tego zbioru zadań z roku 1992 nie znalazłem w nim tego zadania. Widać po latach stwierdzono, że zadanie to jest zbyt ambitne jak na szkołę średnią. W każdym razie w moich szkolnych czasach zadawano takie zadania i dlatego jego rozwiązanie znalazło się w moim poradniku.
