Rozwiązanie równania Diraca w jednorodnym polu elektrycznym - część 1

Szczegóły

Kategoria: Równanie Diraca

Opublikowano: środa, 24, luty 2016 16:23

Autor : Janusz Szcząchor

Exact solutions of the Dirac equation in a homogeneous electric field

Abstract: Solutions of the Dirac wave equation representing an electron and a positron moving in a homogeneous electric field are obtained. The spinor representation is applied. The wave functions are nonstationary. D’Alembert’s method of solving second order partial differential equations is used. Nonexplicit expressions of energy and momentum are obtained. The expressions are relativistically correct.

§1. Stacjonarne i niestacjonarne rozwiązania równania Diraca

Równanie Diraca może być napisane w formie (1)

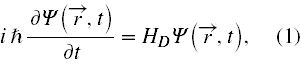
gdzie H_D , to

czyli Dirakowski operator Hamiltona dla naładowanego leptonu poruszającego się w potencjale elektromagnetycznym A^μ = (A₀ , A) [1]. Tutaj jako p został oznaczony (żeby nie dublować symboliki) operator pędu tj.

Ponadto Ψ, to Dirakowski bispinor, a wielkości α i β, to macierze działające w czterowymiarowej przestrzeni spinorowej. Równanie Diraca jest w istocie, przy niezerowym polu elektromagnetycznym, układem czterech równań różniczkowych cząstkowych pierwszego rzędu. Daje się go sprowadzić do układu równań algebraicznych tylko wtedy, gdy położymy A₀ = 0 i A = 0.

Gwoli ścisłości wyjaśniam, że konsekwentnie stosuję metrykę g_μν = (1,-1,-1,-1) i dlatego A₀ = A⁰ , a A_i = - Aⁱ. Ponadto uczulam, że e oznacza ładunek cząstki. Tutaj rozumiemy, że ładunek wzięty jest wraz ze znakiem, tak że dla elektronu e = - |e| [2].

Rozpatrując zagadnienie równania Diraca w jednorodnym polu elektrycznym przyjmujemy A = 0, natomiast A₀ ≠ 0, bo potencjał skalarny jest właśnie źródłem jednorodnego pola elektrycznego. Stąd musimy rozwiązać układ czterech równań różniczkowych cząstkowych, a nie algebraicznych.

W jednorodnym, jak i innym dowolnym polu elektrycznym, którego źródłem jest tylko potencjał skalarny, równanie (1) może być przekształcone [2] w układ równań drugiego rzędu, który przyjmuje postać

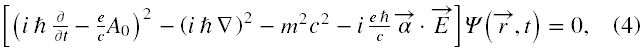
gdzie przedstawienie macierzy α jest jeszcze dowolne.

Z powyższego widać, że w przedstawieniu standardowym ostatni człon równania (4) raczej będzie niediagonalny z uwagi na obecność α. Aby maksymalnie zminimalizować takie trudności powinniśmy użyć spinorowego przedstawienia macierzy Diraca. Mają one wtedy następującą postać

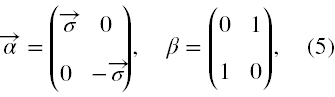
gdzie składowe σ, to macierze Pauliego, a 1 to 2×2 macierz jednostkowa. W ten sposób możemy dalej rozseparowywać równania.

Ponieważ niektóre rozwiązania równania (4) nie spełniają wyjściowego równania (1) i (2), konieczne jest przedstawienie systematycznej metody rozwiązywania równania Diraca w przedstawieniu spinorowym w jednorodnym polu elektrycznym, tak aby móc łatwo wyselekcjonować te rozwiązania równania (4), które spełniają równanie (1) i (2).

Rozłóżmy zatem bispinor Ψ(r ,t) na dwa spinory jak niżej

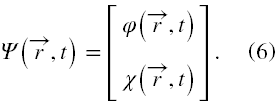
Wówczas równanie Diraca (1) i (2) może być przedstawione używając (6), jako układ dwóch sprzężonych równań różniczkowych. Stąd otrzymujemy (patrz → dodatek matematyczny nr 1)

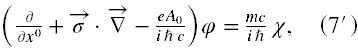
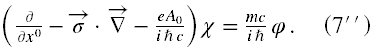
Tutaj opuściliśmy na razie argumenty przestrzenno-czasowe oraz użyliśmy, z uwagi na równość x₀ = x⁰ , dla lepszej estetyki oznaczenia

x⁰ = ct . (8)

Pomnóżmy równania (7) stronami przez iħ/mc i wprowadźmy następujące oznaczenia

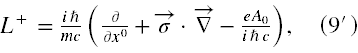
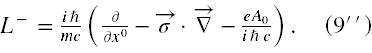
Dzięki powyższemu możemy równania (7) zapisać symbolicznie jako

układ dwóch sprzężonych równań.

Jeżeli równanie (10') potraktujemy jako wzór na funkcję χ i podstawimy je do (10'') właśnie za χ, to otrzymamy równanie II rzędu tylko na φ, które teoretycznie powinno już dać się rozwiązać. Podobnie można postąpić z funkcją φ w równaniu (10'') i podstawiając do (10') otrzymać równanie tylko na χ. Stąd otrzymujemy dwa układy równań określających rozwiązania równania Diraca (1) w jednorodnym polu elektrycznym, a mianowicie

Oraz

Równania drugiego rzędu obu układów są od siebie niezależne, bo z uwagi na niekomutację operatorów (9') i (9") są to dwa różne równania. Jednak układ równań (11), jak i układ równań (12), każdy z osobna, są całkowicie równoważne wyjściowemu równaniu Diraca w polu nie tylko potencjału A⁰, ale i całego A^μ (gdybyśmy nie pominęli w rozważaniach A), patrz [3]. Dlatego rozwiązując którykolwiek z nich powinniśmy otrzymać pełen zbiór rozwiązań.

Sądzę, że nadszedł już czas, aby przeprowadzić poważniejszą dyskusję otrzymanych równań potrzebną szczególnie osobom słabo obeznanym z relatywistyczną mechaniką kwantową. Na ogół wiadomo, że swobodne równanie Diraca ( przecież niezawierające ładunku elektrycznego ) ma rozwiązania o dodatniej energii przypisywane elektronom oraz o ujemnej energii przypisywane pozytonom. Jednak trzeba sobie zdawać sprawę, że zarówno elektron, jak i pozyton mają ładunek elektryczny w każdej sytuacji fizycznej. Tym bardziej tutaj, w jednorodnym polu elektrycznym nie można go pominąć.

Elektron i pozyton mają ładunki elektryczne przeciwnych znaków. W dotychczas zapisanych równaniach, zgodnie z uwagą wskazaną wyżej e oznacza ładunek elektryczny wzięty wraz ze znakiem. Oznacza to, że aby otrzymać równania dla elektronu trzeba za e podstawić -|e|, a dla pozytonu +|e|.

Zauważmy zatem, że z układów równań (11), jak i (12) można otrzymać równania dla elektronu, jak i dla pozytonu. Zważmy ponadto, że - patrz [4] - zarówno równania elektronowe, jaki pozytonowe mają rozwiązania o dodatniej oraz o ujemnej energii. Teraz w tej zmienionej sytuacji okazuje się, że niezależnie od rodzaju cząstki rozwiązania o dodatniej energii odpowiadają tej cząstce, a o ujemnej jej antycząstce. Co zatem zrobić z taką ilością równań?

W tym miejscu przypomnijmy sobie po pierwsze, że pracujemy w przedstawieniu spinorowym. Po drugie w miarę przybywania treści niniejszego opracowania stanie się jasne, że będziemy musieli w pewnym momencie skonfrontować otrzymane rozwiązania z rozwiązaniami swobodnymi, oczywiście w tymże samym przedstawieniu. A jak wyglądają te spinorowe rozwiązania swobodne?

Można znaleźć w [5], że w przeciwieństwie do przedstawienia standardowego to przedstawienie nie różnicuje podziału składowych bispinora na duże i małe składowe. Między rozwiązaniem swobodnym, a w jednorodnym polu elektrycznym powinno być dużo podobieństwa wszak oba ruchy, to ruchy prostoliniowe.

W przedstawieniu spinorowym rozwiązania swobodne zawierają na pierwszej lub drugiej pozycji 1, a na przeciwnej 0. Z kolei na 3 lub 4 pozycji jest wyrażenie, które dla p → 0 zmierza albo do ±1, albo do 0. To wyrażenie, które zmierza do 0 dla cp « mc² powinno być bardzo małe.

Przyjrzyjmy się równaniom (9), oba operatory L⁺, jak i L^– zawierają czynnik ħ/mc. W [2] można znaleźć na samym początku książki, że jest to comptonowska długość fali elektronu równa 3,862·10^–14 m (w jednostkach podstawowych SI).

Zatem powinniśmy wybrać taki układ równań spośród (11) i (12), który pozwoli nam potraktować składową φ jako rzędu 1, tak żeby któryś z elementów χ miał szansę być mniejszego rzędu. A zatem widać, że powinniśmy spróbować rozwiązać układ równań (11), bo wtedy operator L⁺ ma szansę zmniejszyć składową χ względem φ. Podstawiając za e wartość -|e| otrzymamy równanie dla elektronu. Jeżeli znajdziemy jego rozwiązania o dodatniej energii, to przypiszemy je elektronowi, a jeżeli dodatkowo znajdziemy rozwiązania o ujemnej energii to postaramy się je przypisać pozytonowi, a następnie wszystkie rozwiązania skonfrontujemy z rozwiązaniami swobodnymi.

Dokonując odpowiednich przekształceń matematycznych w równaniu II rzędu w układzie równań (11) ( patrz → dodatek matematyczny nr 2 ) otrzymujemy następujące równanie

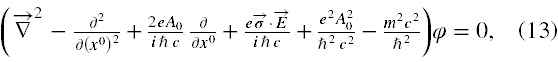
które wraz z drugim równaniem ( I rzędu na χ ) w (11) jest całkowicie równoważne wyjściowemu równaniu Diraca (1)-(2).

Prawdę mówiąc równanie (13) powinno jeszcze zawierać człon e/iħc(∂A₀/∂x⁰), jednak wyraz ten jest równy 0, bo w tym przypadku potencjał skalarny nie zależy od czasu.

Poszukując rozwiązań równań kwantowych w pierwszym rzędzie próbujemy odpowiedzieć na pytanie, czy ma ono rozwiązania stacjonarne? Znajdowanie takich rozwiązań jest stosunkowo łatwiejsze od wszystkich innych. Aby odpowiedzieć na takie pytanie w stosunku do równania (13) zwróćmy uwagę, że jest to równanie hiperboliczne i musimy w tym celu użyć metody Fouriera [6]. Dlatego powracamy do jawnego zapisu zmiennych niezależnych w φ i spróbujemy zapostulować, że równanie (13) ma rozwiązanie o zmiennych rozdzielonych w formie

φ(r,t) = X(r)T(t). (14)

Podstawiamy zatem wyrażenie (14) do (13), następnie dzielimy równanie (13) stronami przez X(r)T(t) i sprawdzamy, czy można rozdzielić człony równania tak, aby po jednej stronie równości były człony zależne tylko od r, a po drugiej tylko od t. Oto wynik powyższej roszady (w potencjale A₀ jawnie zaznaczyłem zmienną r)

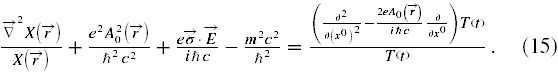
Z równania (15) widać, że po jego prawej stronie jest jeden przeszkadzający człon, czyli

który miesza zmienne r i t, a zatem nie pozwala na istnienie rozwiązania o rozdzielonych zmiennych. Tym samym równanie (13) nie powinno posiadać rozwiązań stacjonarnych!

Jednak wiemy, że równanie Diraca posiada stacjonarne rozwiązania chociażby w polu Kulombowskim. Więc jak to jest?

Otóż jak jest to wyjaśnione np. w [16], w polu elektrostatycznym o symetrii sferycznej hamiltonian Diraca (2) można zapisać jako

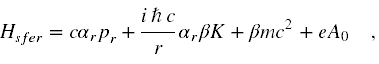
gdzie K jest pewnym operatorem, który komutuje z α_r, β oraz p_r. Ma on wartości własne, którymi są liczby całkowite różne od zera. Operator K komutuje z takim hamiltonianem Diraca

[ K, H_sfer ]₋ = 0.

Stąd istnieje reprezentacja (czyli baza funkcji falowych w przestrzeni Hilberta), w której oba są diagonalne. A zatem w polu Kulombowskim jądra atomowego (najlepiej, gdy można je uznać za punktowe) hamiltonian Diraca ma wartości własne, a równanie (1) ma stany stacjonarne. Po szczegóły odsyłam do [16] lub innych podręczników relatywistycznej mechaniki kwantowej.

Co do potencjału liniowego, to zawsze możemy tak obrócić układ współrzędnych, że potencjał ten będzie zależał tylko od jednej współrzędnej, na przykład x. Wtedy równanie (15) będzie faktycznie ze sobą wiązać wielkości zależne tylko od zmiennych x i x⁰, a E będzie stałym wektorem. W ten sposób równanie (15) zależne faktycznie tylko od dwóch zmiennych jest dowodem na to, że w jednorodnym polu elektrycznym równanie Diraca nie posiada rozwiązań stacjonarnych, bo nie ma dodatkowej symetrii, która pomogłaby zdiagonalizować hamiltonian Diraca (2).

Ponieważ w literaturze naukowej zdarzały się doniesienia, że w jednorodnym polu elektrycznym czy to równanie Diraca, czy już to równanie Schrödingera mają takie stacjonarne rozwiązania muszę w tym miejscu uczynić dygresję i odnieść się do nich.

Najpierw weźmy pod uwagę podręcznik Landaua i Lifszyca [7]. Zacytujmy za nim, że bierzemy pod uwagę ruch cząstki o ładunku e znajdującej się w jednorodnym polu elektrycznym. Jako kierunek pola przyjmiemy oś x i niech F oznacza siłę działającą w tym polu na cząstkę. Zakładając, że pole to ma natężenie E (tutaj to pewna stała), to siła ta wynosi F = eE.

Można przyjąć, że energia potencjalna tej cząstki w tym polu to U = −Fx. Poszukując według przepisu (14) rozwiązań stacjonarnych równania Schrödingera w tym polu (patrz → dodatek matematyczny nr 3) stwierdzamy, że istotnie ma ono rozwiązania stacjonarne. Jeszcze raz zacytujmy autorów, że poziomy energetyczne równania będą tworzyć widmo ciągłe obejmujące cały przedział wartości od −∞ do +∞, wszystkie wartości własne są niezdegenerowane i odpowiadają ruchowi ograniczonemu od strony x = −∞ i nieograniczonemu w kierunku x= +∞.

Skąd ta sprzeczność?

Odpowiedź jest oczywista. Równanie Schrödingera zawiera pochodną po czasie funkcji falowej w pierwszej potędze, a zatem i potencjał skalarny wchodzi do niego w pierwszej potędze. Równanie (13) przeciwnie zawiera w sobie relatywistyczną formułę łączącą pęd i energię relatywistyczną, zatem zawiera drugą potęgę potencjału skalarnego, a stąd i wyraz mieszający zmienne przestrzenne z czasową. Dokładnie tak jak we wzorze skróconego mnożenia (a+b)² pojawia się człon 2ab.

Jednak ruch ładunku elektrycznego w jednorodnym polu elektrycznym powinien być zjawiskiem istotnie relatywistycznym i tutaj użycie równania Schrödingera jest moim zdaniem nieadekwatne, i nie może dać poprawnych fizycznie rozwiązań, mimo matematycznej poprawności prowadzonych obliczeń. To nie powinno dziwić skoro wiemy, że akceleratory liniowe potrafią rozpędzić cząstki do prędkości porównywalnych z c.

Jeśli chodzi o samo równanie Diraca, to wiele można dowiedzieć się z [8]. Wszystko zaczęło się od słynnej pracy dotyczącej paradoksu Kleina [9]. Z uwagi na otrzymany w niej wynik, że prostokątna bariera potencjału elektrycznego o dostatecznie dużej wysokości jest źródłem nadprogramowego prądu, w tym pochodzącego od stanów o ujemnej energii zaczęto poszukiwać i badać rozwiązania równania Diraca w różnych potencjałach, zwłaszcza o mniej gwałtownym skoku.

Pierwszym był Sauter [10], który rozważył potencjał liniowy o następującej złożonej postaci

V = 0,

dla x ≤ 0, oraz

V(x) = νx,

dla 0 < x < L i w końcu

V = νL,

dla x ≥ L, gdzie ν to pewna stała. Następnie założył on rozwiązanie postaci

φ = exp[i/ħ(yp_y + zp_z - Et)]χ(x)

i tak postulowane rozwiązanie po prostu wstawił do równania Diraca I rzędu i je rozwiązał.

Z kolei Plesset [11] rozważył potencjał V jako wielomian dowolnego stopnia względem x w formie

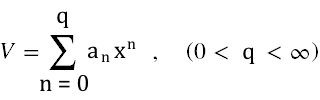
i ponownie szukał rozwiązania równania Diraca I rzędu w formie zapostulowanej przez Fritza Sautera.

Obaj wskazani wyżej autorzy założyli w swoich rachunkach A = 0, ale żaden z nich nie badał, czy w potencjale liniowym, jaki przyjęli dla równania Diraca I rzędu w ogóle są dopuszczalne rozwiązania stacjonarne. Jak udowodniłem wyżej akurat w tym potencjale równanie Diraca nie ma rozwiązań stacjonarnych, a przeprowadzone przez nich dla tego potencjału rachunki uważam za bezprzedmiotowe.

Z uwagi na to co podałem w [12] w Dodatku matematycznym nr 2, że w przedstawieniu standardowym w przypadku braku stanów stacjonarnych nie jest możliwe proste rachunkowo przejście od równań 1 i 2 do układów równań 11, czy 12, wykonywanie dalszych rachunków nastąpi w przedstawieniu spinorowym.

Dodatek matematyczny nr 1

W równaniu Diraca (1) i (2) dokonujemy podstawienia A = 0 oraz opuszczamy argumenty i mamy

oraz dokonujemy kolejnych podstawień

po których otrzymujemy

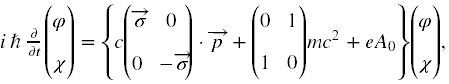
następnie za p podstawiamy jawnie ten operator, czyli

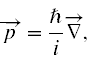
i mamy w końcu równanie

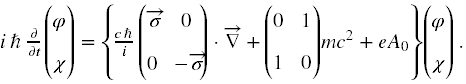
Równanie dzielimy stronami przez ħci oraz ct zapisujemy jako x₀. Następnie przenosimy człony diagonalne na lewą stronę i jest

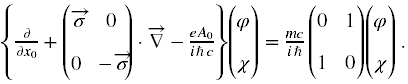
Jak widać macierz β (w tym przedstawieniu) jest jedynym w tym równaniu elementem niediagonalnym, który miesza ze sobą składowe spinorowe. Równanie to możemy już rozdzielić na dwa równania sprzężone na składowe spinorowe φ i χ, otrzymujemy wtedy równania (7).

Dodatek matematyczny nr 2

A zatem przechodzimy do równania II rzędu w układzie (11), podstawiamy jawnie operatory L⁻ i L⁺, wymnażamy przez siebie składniki, dokonujemy redukcji wyrazów podobnych i otrzymujemy następującą postać operatora L⁻L⁺φ

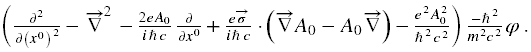
Ponieważ w wyrażeniu

operator nabla działa na iloczyn funkcji, więc po redukcji wyrazów podobnych w wewnętrznym nawiasie pozostaje jedynie wyraz

który jest równy −Eφ.

Wstawiamy następnie powyższe wyrażenie do równania II rzędu w (11), tak otrzymane równanie dzielimy stronami przez −ħ²/m²c² oraz przenosimy jedyny wyraz znajdujący się po prawej stronie ze zmienionym znakiem na lewą, tak aby po prawej było tylko 0, mnożymy równanie stronami przez −1 i ostatecznie otrzymujemy równanie różniczkowe II rzędu na φ

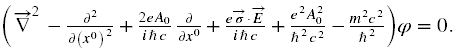
Dodatek matematyczny nr 3

Jeżeli jednorodne pole elektryczne jest skierowane wzdłuż osi x, to energia potencjalna cząstki w tym polu ma postać U = − Fx (gdzie F = eE, a e to ładunek cząstki) i równanie Schrödingera dla tej cząstki ma poniższą formę

Niech Ψ = T(t)·X(x), wstawmy to do powyższego równania, wykonujemy różniczkowania, a następnie dzielimy stronami tak otrzymane równanie przez tenże iloczyn funkcji i próbujemy skrócić licznik i mianownik tam, gdzie to jest możliwe. Powinniśmy otrzymać następujący wynik

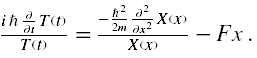
Jak widać z powyższego takie równanie Schrödingera da się rozseparować, każdą ze stron powyższej równości możemy przyrównać do stałej separacji, którą oznaczymy jako E i jest nią po prostu energia stanu stacjonarnego. W ten sposób otrzymujemy równanie (24.1) w [7]

LITERATURA

[1] J. D. Bjorken, S. D. Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985, §1.4 .

[2] W. B. Bierestecki, E. M. Lifszyc, L. P. Pitajewski, Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §32.

[3] I. Białynicki-Birula, Z. Białynicka-Birula, Elektrodynamika kwantowa, PWN, Warszawa 1974, §16.

[4] J. D. Bjorken, S. D. Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985, rozdział 5 .

[5] J. Szcząchor, Metody rozwiązywania równania Diraca - Część 1.

[6] W. Pogorzelski, Analiza matematyczna, Tom IV, PWN, Warszawa 1956, część 10, §24.

[7] L. D. Landau, E. M. Lifszyc, Mechanika Kwantowa - teoria nierelatywistyczna, PWN, Warszawa 1979, rozdział III, §24. Ruch w polu jednorodnym.

[8] A. Calogeracos, N. Dombey, History and Physics of the Klein Paradox, arXiv:quant-ph/9905076v1.

[9] O. Klein, Z. f. Physik 53, 157 (1929).

[10] F. Sauter, Z. f. Physik 69, 742-764(1931), Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs.

[11] M. S. Plesset, The Dirac Electron in Simple Fields, Physical Review 41, 278 (1932).

[12] J. Szcząchor, Metody rozwiązywania równania Diraca - Część 2.

[13] W. Pogorzelski, Analiza matematyczna, Tom IV, PWN, Warszawa 1956, część 10, §4,§21-23,§25.

[14] W. I. Smirnow, Matematyka wyższa, Tom II, PWN,Warszawa 1963, rozdział VII, §17.164.

[15] W. B. Bierestecki, E. M. Lifszyc, L. P. Pitajewski, Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §40.

[16] B. Średniawa, Mechanika kwantowa, PWN, Warszawa 1981.