W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 8

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano:sobota, 29, grudzień 2018 18:40

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 3.81, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

W pewnej odległości od Ziemi różnica potencjałów grawitacyjnych dwu punktów leżących na jednej linii ze środkiem Ziemi i odległych od siebie o l wynosi ΔV. Wyraź odległość tych punktów od powierzchni Ziemi. Promień Ziemi jest także dany i wynosi R.  » Rozwiązanie

zadanie nr 3.196, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

Tak zwany satelita stacjonarny Ziemi porusza się po orbicie kołowej w płaszczyźnie równika z zachodu na wschód. a) W jakiej odległości od powierzchni Ziemi i b) z jaką prędkością powinien się poruszać, aby dla obserwatora dla Ziemi wydawał się nieruchomy? Promień Ziemi R = 6370 km, przyspieszenie ziemskie g = 9,8 m/s², długość doby T = 86 400 s.  » Rozwiązanie

Uwaga wstępna

W dalszym ciągu będziemy korzystać z własności, że jednorodna kula (czyli mająca stałą gęstość) oddziaływuje grawitacyjnie z punktem materialnym tak, jakby cała jej masa była skoncentrowana w jej środku. Więcej na ten temat podaliśmy przy okazji rozwiązywania zadań numer 3.9 i 3.10 z tegoż zbioru Mendla (¹).

Rozwiązanie zadania nr 3.81 ¹

Rozwiązanie zadania zacznijmy od rysunku sytuacyjnego, rys. nr 1.

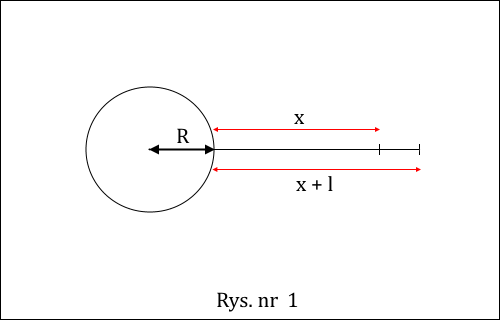
Potencjał grawitacyjny wytworzony przez Ziemię w odległości x od jej powierzchni, zgodnie ze wskazaną na wstępie zasadą jest równy

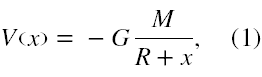
a w odległości x + l

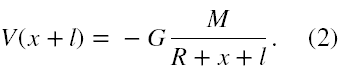
Potencjał grawitacyjny w odległości x + l jest większy od tego dla odległości x. Podana różnica potencjałów ΔV raczej powinna być dodatnia, więc podstawowe równanie opisujące założenia tego zadania powinno mieć postać

Stąd otrzymujemy jawnie do rozwiązania następujące równanie na nieznaną wielkość x

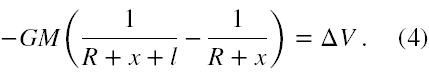
W nawiasie w (4) ułamki doprowadzamy do wspólnego mianownika (R + x)·(R + x + l), odwracamy otrzymaną proporcję, przekształcamy i otrzymujemy równanie kwadratowe na x w formie

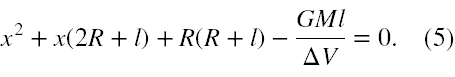
Współczynniki trójmianu kwadratowego są postaci

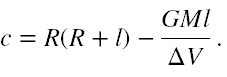
Obliczamy deltę (człony z R² i Rl się skracają)

Δ = b² - 4ac = l² + 4GMl/ΔV . (6).

Rozwiązania są dwa, dane wzorem

x_1/2 = ( - b ± √Δ )/2a,

w postaci (po wykonaniu w liczniku dzielenia przez 2 z mianownika)

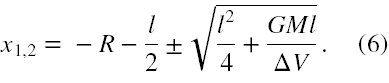
Ponieważ otrzymane x musi być większe od zera, więc prawidłowym rozwiązaniem jest ten wynik w (6), który ma '+' przed znakiem pierwiastka kwadratowego.

Chociaż w zadaniu nie ma podanych konkretnych wartości liczbowych dla danych, to jednak prawidłowe postępowanie powinno polegać na zbadaniu dla konkretnych wartości jaka jest wartość liczbowa delty.

Rozwiązanie zadania nr 3.196 ²

Zacznijmy od uwag ogólnych co do treści zadania. Nie powinno nikogo dziwić, że satelita ma się poruszać z zachodu na wschód, bo Ziemia właśnie porusza się w ten sposób (przeciwnie do pozornego ruchu Słońca na niebie) (²).

Po drugie, nie powinna nikogo zmylić podana wartość przyspieszenia ziemskiego. Jest to wartość na powierzchni Ziemi, a nie na orbicie, po której porusza się satelita. Użyte w zadaniu sformułowanie oznacza, że mamy takiej wartości g użyć w rozwiązaniu jako danej. Spójrzmy na rysunek sytuacyjny zadania - rys. nr 2.

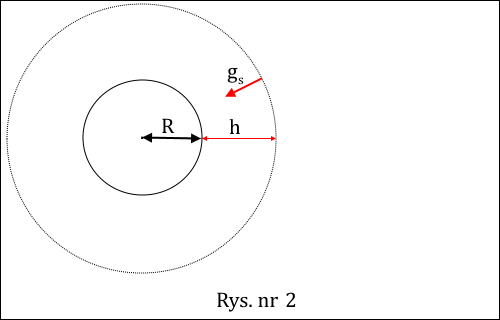
Wartość liczbowa przyspieszenia grawitacyjnego jakie odczuwa satelita, to

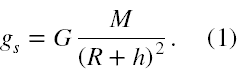
Zgodnie z tym, co wyżej wskazałem mamy obecny w (1) iloczyn GM wyrazić poprzez g. Jest to możliwe na podstawie wzoru na g, czyli

g = GM/R² . (2)

W ten sposób wartość g_s jest dana jako

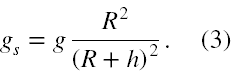
Możemy już teraz przejść do problemu orbity satelity. W tak uproszczonym zagadnieniu oczywiście pomijamy problem ewentualnego oporu górnych warstw atmosfery. W warunkach tego zadania satelita będzie geostacjonarny, jeżeli dodatkowo jego okres obiegu będzie równy okresowi obrotu Ziemi wokół jej osi.

Orbita satelity będzie stabilna, jeżeli cała siła przyciągania grawitacyjnego będzie siłą dośrodkową zmuszającą satelitę do ruchu po tej orbicie. Oznacza to równość przyspieszeń grawitacyjnego i dośrodkowego

g_s = a_r . (4)

Z uwagi na to, że w zadaniu mamy jako daną długość doby ziemskiej, więc naturalniej będzie wykorzystać wzór na przyspieszenie dośrodkowe zawierający prędkość liniową satelity

a_r = v²/(R + h) . (5)

Prędkośc liniową satelity na jego orbicie znajdziemy dzięki temu, że jego droga w ciągu jednego okresu obiegu to obwód koła o promieniu R + h, czyli v = 2π(R+h)/T. Stąd wzór (5), po stosownej redukcji, daje nam

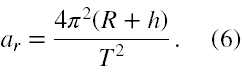
Podstawiając wzory (3) i (6) do (4) otrzymujemy

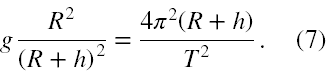
Tak otrzymaną proporcję przekształcamy w celu otrzymania wzoru na (R + h)³, otrzymany wzór następnie pierwiastkujemy sześciennie stronami, wybieramy wynik dodatni oraz w końcu otrzymujemy, że

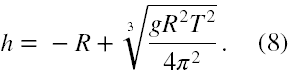
Aby otrzymać wzór na prędkość liniową satelity na orbicie do wzoru v = 2π(R+h)/T podstawiamy za (R + h), to co wyliczyliśmy wyżej z obliczenia pierwiastka sześciennego i mamy

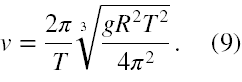
(¹) Szczegółowy dowód tego faktu można znaleźć w - D. Halliday, R. Resnick, Fizyka tom I, rozdział 16-6, PWN, Warszawa 1973.

(²) Najwyraźniej w roku 1976 nie istniało jeszcze słowo 'geostacjonarny'.