Rachunek wektorowy w fizyce szkolnej - część 1

Szczegóły

Kategoria: Fizyka szkolna

Opublikowano: niedziela, 29 grudzień 2019 16:10

Autor : Janusz Szcząchor

Po przejrzeniu obecnie obowiązujących podręczników z fizyki dla szkół średnich (różnych wydawnictw) dostrzegłem bardzo poważną powierzchowność w programie nauczania co do sposobu wdrażaniu rachunku wektorowego. Jako przykład mogę podać brak dokładnego wyjaśnienia czym różni się pojęcie współrzędnej punktu od współrzędnej wektora, jaka jest różnica między długością wektora, a jego współrzędną. Wątpię, aby uczniowie wynieśli tę wiedzę z lekcji matematyki w szkole podstawowej.

W mojej ocenie przydałoby się jakieś korepetytorium z tej dziedziny dostosowane do poziomu rozwoju absolwenta podstawówki. W przeciwnym wypadku wielu uczniów będzie miało problem ze zrozumieniem tych zagadnień. Wątpię, czy nauczyciele będą mieli czas na lekcji, aby wyjaśniać uczniom takie niuanse. Stąd mój poradnik.

Do jego napisania użyłem tu jako przewodnika po materiale nauczania z fizyki w szkole średniej podręcznika - Marcin Braun, Krzysztof Byczuk, Agnieszka Seweryn-Byczuk, Elżbieta Wójtowicz, Zrozumieć Fizykę 1, Podręcznik dla szkół ponadgimnazjalnych, Zakres rozszerzony, Nowa Era, Warszawa 2016.

§1 Wstęp

W szkole uczy się posługiwania wektorami dość wcześnie. Już w szkole podstawowej na lekcjach fizyki (abstrahuję tutaj od tego, co jest na lekcjach matematyki) mówi się uczniom, że wektor to taki odcinek skierowany, taka strzałka oraz podaje się, że ma on punkt przyłożenia, kierunek, zwrot i wartość (wraz z definicjami co to jest). Uczy się rysować taki odcinek, zaznaczać jego punkt przyłożenia, rysować jego długość w pewnej skali, czyli podawać jego wartość.

Z drugiej strony uczy się co to jest droga, jak liczyć prędkość, przyspieszenie. Póki przykłady są bardzo proste i nie trzeba wykorzystywać wektorowych własności tych wielkości nie ma większych problemów.

Problemy się pojawiają w szkole średniej, gdy nie da się już ignorować własności wektorowych takich wielkości, na przykład podczas rozpatrywania ruchu jednostajnie przyspieszonego czy opóźnionego. Nie wystarcza już wtedy opis graficzny wektorów, potrzebny jest ich opis algebraiczny do prowadzenia obliczeń, sporządzania wykresów zależności tych wielkości od czasu, ich interpretowania.

Niniejszy artykuł ma pomóc uczniom w zapoznaniu się z językiem algebraicznym opisu wektorów, jego zrozumieniu w intuicyjny sposób. Będę starał się przedstawić elementarne podstawy tej teorii na naprawdę prostych przykładach pochodzących wprost z zagadnień fizyki w szkole średniej.

§2 Wektory geometryczne

Wektory mogą być bardzo różne. Takich których nie da się narysować jest więcej niż te, które się da. Ale nie ma obawy, będziemy się zajmować tylko takimi wektorami, które rysowałeś już w szkole podstawowej. Nazywają się one wektorami geometrycznymi [1]. Narysujmy zatem na początek jeden taki wektor, w mniej więcej ten sposób, jak mnie uczono tego w 6 klasie szkoły podstawowej (rys. nr 1). Będzie to wektor siły o wartości 25 N.

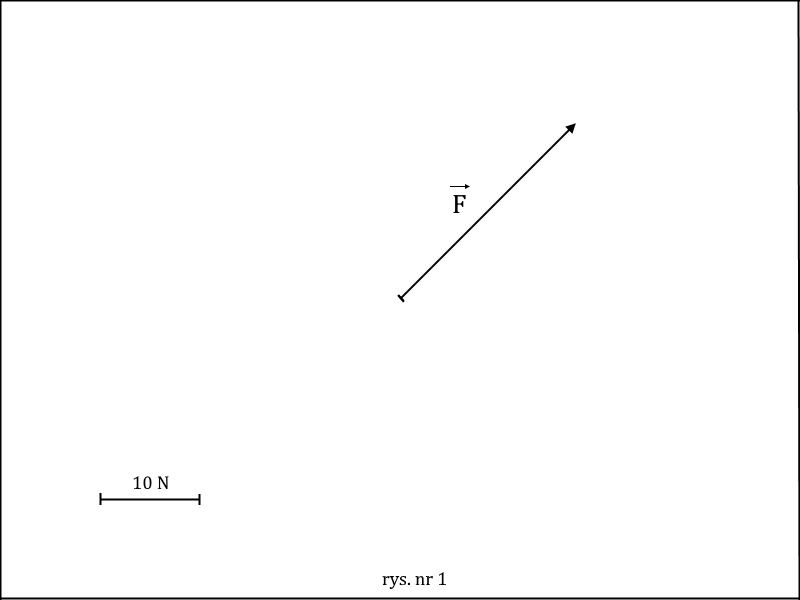
Ile jest wektorów geometrycznych? Oczywiście nieskończenie wiele. Co można robić z wektorami?

1. Dodawanie wektorów - w jego wyniku otrzymujemy nowy wektor, zwany wektorem wypadkowym. Można to robić geometrycznie zgodnie z regułą równoległoboku lub trójkąta, albo algebraicznie.
   
   Jeżeli do wybranego wektora dodamy taki inny wektor, że w wyniku otrzymamy wektor zerowy, to ten drugi wektor nazywamy przeciwnym w stosunku do tego pierwszego. Otrzymujemy go z tego pierwszego poprzez zmianę jego zwrotu na przeciwny.
   
   Nie definiuje się odejmowania wektorów. Jest to działanie będące odmianą dodawania wektorów polegające na dodaniu do danego wektora innego wektora, ale o przeciwnym zwrocie w stosunku do zwrotu wektora, którego chcemy odjąć.
2. Mnożenie wektora przez liczbę. W wyniku otrzymujemy nowy wektor, którego długość jest tyle razy większa od długości starego ile wynosi liczba, przez którą mnożymy, a punkt przyłożenia, kierunek oraz zwrot pozostają bez zmiany.
   
   Jeżeli liczba pochodzi z przedziału od 0 do 1, to otrzymujemy wektor odpowiednio krótszy.
   
   Wymnożenie wektora przez liczbę ujemną daje w wyniku wektor o zwrocie przeciwnym do danego.
   
   Nie definiuje się dzielenia wektora przez liczbę. Należy to traktować jako mnożenie wektora przez odwrotność liczby, przez którą chcemy go podzielić.
   
   Można pomnożyć wektor przez 0. Otrzymujemy wtedy wektor zerowy, którego długość jest oczywiście równa 0.
3. Z dwóch wektorów można otrzymać ich iloczyn skalarny, który jest liczbą.
4. Z dwóch wektorów można otrzymać ich iloczyn wektorowy, który jest wektorem.

W podręcznikach fizyki do liceum próbuje się stosować obliczenia algebraiczne na wektorach i w tym celu wprowadza się pojęcie współrzędnej wektora. Niestety robi się to przy pomocy rysunków, nie wyjaśniając co to faktycznie jest. Zajmiemy się tym w następnym paragrafie.

§3 Współrzędna wektora

Współrzędne wektora geometrycznego można ustalić dopiero po wprowadzeniu układu współrzędnych (a dla fizyka układu odniesienia) w przestrzeni, w której posługujemy się tymi wektorami. Szczególne zalety tego zabiegu są widoczne w przestrzeni stereometrycznej (trójwymiarowej).

Następnie trzeba wybrać zbiór wzorcowych wektorów w przestrzeni, w której chcemy prowadzić obliczenia. Z kolei korzystając z możliwości mnożenia wektorów przez dowolną liczbę rzeczywistą oraz ich dodawania do siebie możemy z tychże wektorów wzorcowych 'uzyskać' dowolny inny wektor. W przestrzeni trójwymiarowej potrzeba na to trzech wektorów wzorcowych (fachowo nazywanych bazowymi).

Jednak, aby nie odbiegać zanadto od problemów mechaniki w liceum będziemy się często ograniczać do zbioru wektorów na prostej, czyli w jednym wymiarze.

Na prostej potrzeba do tego tylko jednego wektora wzorcowego (bazowego). Może to być w zasadzie dowolny wektor, ale dla wygody i prostoty obliczeń wybiera się wektor o długości równej 1.

Możemy go zaczepić w dowolnym punkcie osi X, ale na początek zaczepmy go w początku układu współrzędnych. Nazywamy go wersorem osi X. Jest on 'nośnikiem' kierunku i zwrotu tej osi. Są różne sposoby jego oznaczania.

My oznaczymy wersor osi X jako i. Wtedy dowolny wektor r o punkcie zaczepienia w początku układu współrzędnych (punkt o położeniu 0 na naszej osi X) możemy zapisać jako

r = ix, (1)

gdzie x, to współrzędna wektora r (¹) określona względem wybranego wersora i. Przesuwając ten wersor w dowolne miejsce na osi X możemy tak zapisać dowolny wektor leżący na tej osi, patrz rysunek nr 2.

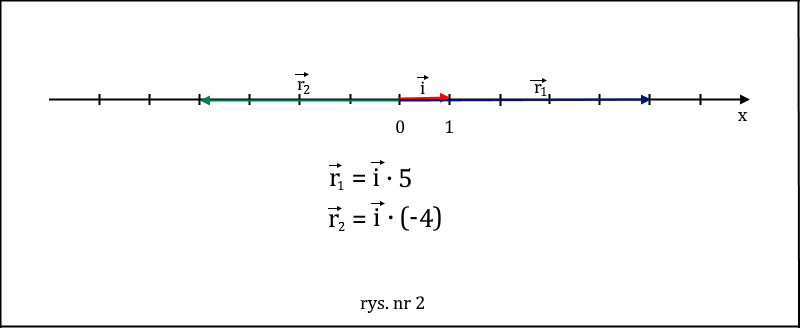
Współrzędna wektora musi być liczbą, ale nie musi być stałą. Może być wartością funkcji, na przykład funkcji czasu o wartości w zbiorze liczb rzeczywistych. W ten sposób możemy opisać wektory, których długość zmienia się w czasie.

r(t) = ix(t), (2).

§4 Długość wektora

Nie powinno być wątpliwości co to jest długość wektora, ale jak ją faktycznie obliczyć? Po pierwsze oznaczamy tę wielkość jako wartość bezwględną wziętą z wektora, czyli |r(t)|. A obliczamy ją zgodnie z poniższą regułą

|r(t)| = |i|·|x(t)|, (3),

a ponieważ długość wersora i z wyboru jest równa 1, więc

|r(t)| = |x(t)|, (4).

Tutaj symbol |x(t)| należy traktować jako wzięcie zwykłej wartości bezwzględnej z wartości współrzędnej wektora. Widzimy, że długość wektora jest wielkością nieujemną (²), co wynika z własności wartości bezwzględnej, przeciwnie do współrzędnej, która może być ujemna. Teraz przejdziemy do przykładów z fizyki szkolnej, aby zobaczyć jak się posługiwać pojęciem współrzędnej w praktyce.

§5 Wektor położenia punktu materialnego

Ponieważ patrzymy na te sprawy z punktu widzenia fizyka (a nie matematyka) to od razu zakładamy, że wybraliśmy jakiś konkretny układ odniesienia i wszystkie rozważania prowadzimy właśnie w nim. Układ współrzędnych składający się na ten układ odniesienia musi mieć wybraną jednostkę długości na swoich osiach. Położenie punktu materialnego możemy opisywać na dwa sposoby.

Pierwszy polega na podaniu jego współrzędnych jako punktu matematycznego w układzie współrzędnych związanym z wybranym układem odniesienia, patrz rysunek nr 3 (dla lepszej poglądowości użyjemy tu układu współrzędnych na płaszczyźnie).

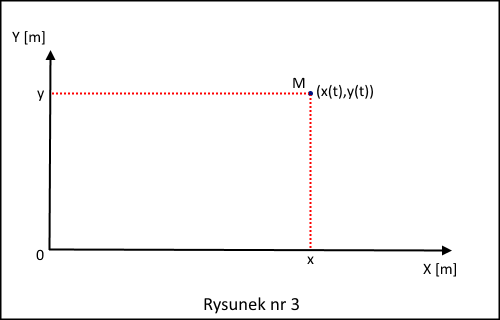
Te współrzędne, to x(t) i y(t).

Drugi sposób polega na użyciu wektora położenia punktu materialnego. Wektor położenia punktu materialnego, to wektor łączący początek wybranego układu współrzędnych z miejscem, w którym ten punkt materialny się znajduje, patrz rysunek nr 4.

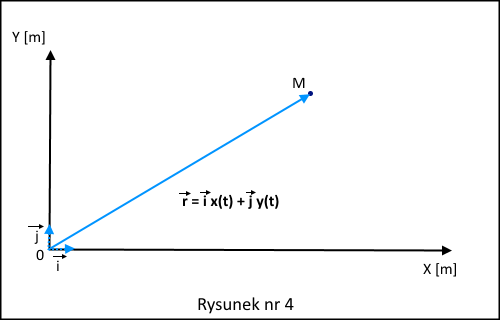
Tutaj współrzędne, to ponownie x(t) i y(t), te same co wyżej, ale teraz są współrzędnymi wektora położenia r względem wersorów i na osi X oraz j na Y.

Wektor położenia punktu materialnego oznaczamy zawsze jako r. Gdyby było więcej punktów materialnych, ich wektory oznaczamy kolejnymi liczbami naturalnymi umieszczonymi jako indeks dolny r₁, r₂ i tak dalej.

W obu przypadkach współrzędne położenia punktu materialnego, jak i współrzędne wektora położenia tego punktu mogą być funkcjami, na przykład funkcjami czasu o wartościach w zbiorze liczb rzeczywistych.

Po co stosuje się aż dwa sposoby?

Zbiór wszystkich punktów matematycznych, w których znajdował się punkt materialny w pewnym przedziale czasu tworzy jego tor ruchu. Jest to krzywa geometryczna jaką zakreśla ten punkt podczas swego ruchu. Podanie jego współrzędnych jako funkcji czasu daje nam równanie jego toru ruchu w formie parametrycznej (parametrem jest czas)

x = x(t), (5)

y = y(t), (6)

z = z(t), (7)

w przypadku, gdyby ruch odbywał się w przestrzeni trójwymiarowej.

Długość fragmentu toru ruchu, na którym ciało nie zawraca (nie cofa się), to droga, patrz rysunek nr 5.

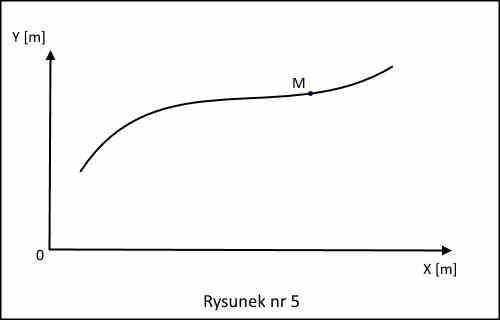
Drugi sposób pozwala nam obliczyć takie wielkości jak prędkość i przyspieszenie punktu materialnego, które są wektorami.

§6 Wektor przemieszczenia punktu materialnego

Wektorem przemieszczenia ciała Δr podczas ruchu nazywamy wektor łączący punkt jego początkowego położenia z punktem jego końcowego położenia. W przypadku ruchu po prostej punkt początkowego położenia to x₁, a końcowego to x₂, patrz rysunek nr 6.

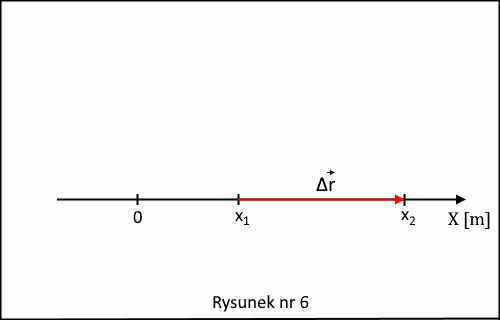
Aby ustalić współrzędną tego wektora wyraźmy go poprzez wektory położenia ciała w punktach x₁ i x₂, rysunek nr 7 (z uwagi na czytelność rysunku wektory te zostały narysowane lekko przesunięte w górę i w dół).

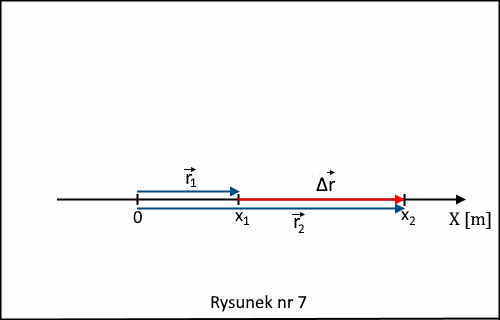
Mamy następującą równość

r₁ + Δr = r₂. (8)

Rozpiszmy wektory na składowe (³), w tym przypadku każdy z nich ma tylko składowe wzdłuż osi X

ix₁ + iΔx = ix₂. (9)

i(x₁ + Δx) = ix₂.

Równość wektorów, z uwagi na identyczne wersory oznacza równość współrzędnych

x₁ + Δx = x₂. (10)

Zatem

Δx = x₂ - x₁. (11)

Wektorowo możemy to zapisać

Δr = r₂ + (- r₁) = r₂ - r₁. (12)

Wektory przemieszczenia jak każde wektory można oczywiście dodawać. Będzie to miało fizyczny sens, gdy dodając do siebie wektory przemieszczeń z kolejnych przedziałów czasu otrzymamy wektor całkowitego przemieszczenia ciała w ciągu łącznego przedziału czasu.

W przypadku ruchu prostoliniowego i pod warunkiem, że ciało nie zawraca długość wektora przemieszczenia jest równa drodze ciała. Na ogół jednak tak nie jest.

Czytaj dalej

(¹) Jeżeli mamy wektor r w przestrzeni trójwymiarowej, to jego rozkład na składowe ma postać
r = ir_x + jr_y + kr_z, gdzie wektory i, j i k, to wersory osi X,Y i Z, a r_x, r_y i r_z, to odpowiednie współrzędne. Jest kilka zwyczajowych sposobów oznaczania wersorów i współrzędnych, patrz np. [2], §1.2 .
Ja w tym artykule będę stosował różne kierując się zasadą jak najbardziej intuicyjnego oznaczania.

(²) W przestrzeni dwuwymiarowej i więcej wymiarowej długość wektora może być dana tzw. metryką kartezjańską. W trzech wymiarach ma ona postać |r| = +((r_x)² + (r_y)² + (r_z)²)^1/2, patrz podręcznik Byrona i Fullera §1.3 .

(³) Zasadniczo pojęcie "rozłożenia" wektora na składowe ma podwójne znaczenie.
Pierwsze oznacza znalezienie takich trzech wektorów, po dodaniu których do siebie otrzymamy z powrotem wektor, który rozkładamy.
Jednak na ogół chodzi nam o to, aby te wektory składowe leżały każdy na innej osi współrzędnych, aby każdy z nich był wyrażony tylko poprzez jeden wersor i jedną współrzędną. Dlatego przez rozłożenie wektora na składowe ma się na myśli na ogół też od razu rozpisanie ich na wersory i współrzędne. Więcej o tym możesz znaleźć w książce Karaśkiewicza [3], w § 12.

BIBLIOGRAFIA

[1] N.W. Jefimow, E.R. Rozendorn, Algebra wraz z geometrią wielowymiarową, §2 - Przykłady przestrzeni liniowych, PWN, Warszawa 1976.

[2] F. W. Byron, R. W. Fuller, Matematyka w fizyce klasycznej i kwantowej, Tom I, PWN, Warszawa 1975.

[3] E. Karaśkiewicz, Zarys teorii wektorów i tensorów, PWN, Warszawa 1974.