Jak opisać oddziaływanie pojedynczego fotonu z materią? - Część 1

Szczegóły

Kategoria: Nowa Fizyka

Opublikowano: środa, 5, sierpień 2015 13:00

Autor : Janusz Szcząchor

Akademickie programy nauczania kwantowej teorii pola elektromagnetycznego przyzwyczajają studiujących do myślenia, że fotony w zasadzie opisuje się tylko falami płaskimi monochromatycznymi [1,2,3,4]. Takie podejście pozwala łatwo uwzględnić zasadę zachowania czteropędu w procesach kwantowych, a zostało wprowadzone przez Diraca w jego słynnej pracy [5].

Jednak już jako student miałem w tym względzie zasadnicze wątpliwości. Fala płaska nie wyróżnia żadnego punktu w przestrzeni, a zatem taki foton faktycznie jest nielokalizowalny. Z drugiej strony, z uwagi na skończoną prędkość światła foton wychwycony przez atom w procesie absorcji musi pochodzić z jego otoczenia, a nie z całej dostępnej przestrzeni.

Widać już stąd, że standardowe metody opisu fotonu są bardzo ułomne. Idąc dalej tym tropem niniejszy artykuł stawia sobie za cel postawienie pytania - jaka jest faktycznie funkcjonalna postać potencjału wektorowego pojedynczego fotonu?

§1. Podstawowe wady opisu pojedynczych fotonów przy pomocy fali płaskiej

Na początek przypomnijmy podstawowe fakty dotyczące fal płaskich monochromatycznych. Zgodnie z [6] mają one poniższą ogólną postać ( tutaj wektor E, to oczywiście wektor natężenia pola elektrycznego ):

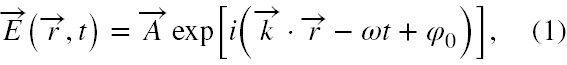
gdzie A - amplituda, k - wektor falowy, ω - częstość i φ₀ - faza początkowa drgań. Ponieważ w tym wzorze r i t nie są ze sobą funkcjonalnie powiązane, więc wielkość (1) opisuje faktycznie nieskończony monochromatyczny ciąg falowy.

Taki obiekt fizyczny ma gęstość energii rozłożoną równomiernie w całej przestrzeni. Jest oczywistym, że z takim obiektem nie można powiązać pojedynczego fotonu, bo takowy powinien mieć energię skoncentrowaną w ograniczonym obszarze. Nie będzie zatem niczym nadzwyczajnym wniosek, że z takim ciągiem powinien być związany bardzo liczny zbiór monochromatycznych fotonów.

Oprócz wątpliwości natury czysto intuicyjnej są także praktyczne dowody, gdy weźmie się pod uwagę sposób wykrywania światła [7]. Niezliczone doświadczenia optyczne wykonywane do połowy XX wieku, w ten czy inny sposób polegały na detekcji światła. Klasycznym przykładem jest tu doświadczenie Younga.

Gdyby światło miało postać monochromatycznej fali płaskiej, to z uwagi na nieskończony czas spójności 2 takich obiektów, interferencję światła możnaby obserwować zawsze. Dlatego już przed narodzinami kwantowej teorii światła wiedziano, że nie istnieją nieskończone ciągi falowe.

Wykorzystanie zjawiska fotoelektrycznego do konstrukcji fotopowielaczy umożliwiło rejestrację pojedynczych fotonów. To z kolei dało możliwość zbadania rozkładu statystycznego fotonów w dowolnej wiązce światła, ale jednocześnie stanowi kolejny dowód, że nie można opisywać pojedynczego fotonu niekończącą się falą.

Rozwój technik laserowych przyspieszył rozwój optyki kwantowej. Skutkiem tego zdefiniowano pojęcie stanu spójnego, obiektu najbardziej zbliżonego do tego co klasycznie uważano za nieskończoną monochromatyczną falę płaską. Jest to nieskończona, o statystyce Poissonowskiej superpozycja stanów zawierających kolejno 0,1,2 aż do +∞ fotonów. Wszystkie stany mają oczywiście tę samą częstość. Natężenie pola elektrycznego takiego obiektu jest właśnie nieskończoną monochromatyczną falą płaską. Gwoli ścisłości zacytuję [16] : “...Stan spójny jest niemal klasyczny, gdyż nie tylko daje właściwą wartość oczekiwaną natężenia pola, lecz zawiera tylko szum próżni. ...“.

W 1935 roku Wołkow [8] podał ścisłe rozwiązanie równania Diraca w polu nieskończonej płaskiej fali elektromagnetycznej.

W pracy [9] pokazano jak policzyć prawdopodobieństwa różnych procesów w polu tej fali takich jak kreacja pary jednym fotonem, jednofotonowej anihilacji pary, czy emisja fotonu przez elektron, a także przy okazji udowodnić istnienie stanów n-fotonowych w płaskiej fali o dużym natężeniu.

Porównując te rachunki z definicją stanu spójnego w sposób oczywisty widać, że nieskończona elektromagnetyczna fala płaska jest stanem spójnym i nie może służyć do opisu swobodnego i odosobnionego fotonu.

Przeliczyłem wyprowadzenie Wołkowa i ustaliłem, że pod działaniem takiej fali bispinor elektronowy opisujący elektron o polaryzacji +1/2 przechodzi w kombinację liniową stanów elektronowych o spinie +1/2 i −1/2 oraz takichże stanów pozytonowych. Aby się o tym przekonać wystarczy poddać ogólne rozwiązanie Wołkowa działaniu operatorów rzutowych na stany o określonym znaku energii i polaryzacji ( dodatek A). Tym samym nie powinno dziwić, że w płaskiej fali elektromagnetycznej są możliwe powyższe procesy.

§2. Czy istnieją pojedyncze i odosobnione fotony?

Postawione powyżej pytanie z pewnością nie jest pytaniem trywialnym. Problem leży w tym, że w doświadczeniach nie możemy użyć dowolnych błąkających się gdzieś po przestrzeni fotonów. Aby móc ich użyć musimy posiadać źródło, które je nam wygeneruje na żądanie i skieruje je do właściwej aparatury. A tylko od cech tego źródła będzie zależeć jaka będzie statystyka fotonów.

Wszystkie klasyczne źródła światła używane w układach doświadczalnych, a mam tu na myśli na przykład lampy rtęciowe mimo, że stosowano w nich różne filtry w dalszym ciągu były źródłem zbyt wielu fotonów, aby można było uznać, że któryś z nich jest pojedynczy i odosobniony. Jest zatem jasne, że do uzyskania pojedynczych fotonów jest potrzebne nowe i rewolucyjne narzędzie.

Nie będę tu robił wykładu, ale podam, że niezależnie od prac doświadczalnych można teoretycznie na podstawie praw mechaniki kwantowej udowodnić, że każdy wzbudzony atom w próżni musi w sposób nieodwracalny oddać energię wzbudzenia i powrócić do stanu podstawowego.

Dość długo myślano, że tak po prostu musi być. Udowodnieniu, że jednak w przyrodzie drzemią inne możliwości przyszła z pomocą wnęka rezonansowa. Każda taka wnęka w sposób istotny modyfikuje rozkład dostępnych stanów dla zamkniętego w niej pola elektromagnetycznego. Zamiast dostępnego w próżni pełnego widma są dostępne tylko częstości rezonansowe. Dzięki temu zamknięcie w niej odpowiednio dobranego atomu mającego pożądaną strukturę poziomów energetycznych może prowadzić do zaniku dla niego emisji spontanicznej.

Z kolei dzięki rozwojowi technik wykorzystujących nadprzewodniki udało się skonstruować wnęki rezonansowe o nadzwyczajnie wysokiej dobroci. Stąd wyemitowany przez jakiś atom w takiej wnęce foton nie będzie natychmiast pochłonięty przez ścianki i będzie mógł bardzo długo przebywać w niej aż ponownie pochłonie go ten atom.

W wyniku rozwoju technik pozwalających na spowalnianie atomów jest możliwe zapewnienie, aby w ciągu dostatecznie długiego czasu w takiej wnęce znajdował się tylko jeden atom. Jeżeli do tego użyjemy w doświadczeniu atomów rydbergowskich, które są faktycznie atomami dwupoziomowymi, to staje się możliwe, że w wyniku emisji spontanicznej takiego atomu przez wystarczająco długi czas we wnęce będzie się znajdował tylko jeden foton!

Dzięki opisanej wyżej technologii dzisiaj jest już możliwe przeprowadzanie doświadczeń nad oddziaływaniem pojedynczych atomów z pojedynczymi fotonami [17].

Nie jest to jedyna technika prowadząca do manipulacji pojedynczymi fotonami. W pracy [10] pokazano jak doświadczalnie zbadać rozkład widmowy jednego fotonu (nie będę tutaj używał fachowych pojęć typu gęstość spektralna itd.). Uzyskano tam praktyczny dowód, że pojedynczy foton nie jest monochromatyczny!

§3. Rozwój metod opisu fal elektromagnetycznych

Do niedawna podstawowym sposobem opisu fal elektromagnetycznych umożliwiającym łatwe znalezienie wszystkich dozwolonych w danym zagadnieniu rozwiązań było zastąpienie równań Maxwella opisujących wektory E i B równaniem falowym na potencjał wektorowy A (a także i φ), w uzupełnieniu B przypominam jego wyprowadzenie. Potencjał ten de facto traktowano jako substytut funkcji falowej fotonu [3], wszakże E.M.Lifszyc użył tam sformułowania, że funkcja falowa fotonu o określonym pędzie k i o określonej polaryzacji ma postać podaną we wzorze (43.9), czyli postać czteropotencjału A^µ .

Fakt, że potencjały A i φ ¹  zgodnie z regułą minimalnego sprzężenia wchodzą do równań kwantowych szczególnie uzasadniał takie postępowanie. Zaniedbywano tutaj fakt, że w przeciwieństwie do pól E i B, potencjały te są wielkościami niemierzalnymi fizycznie. Ponadto nie da się z potencjałów wektorowego i skalarnego skonstruować wielkości, której możnaby nadać interpretację gęstości prawdopodobieństwa.

Jednak od pewnego czasu zaczęto poszukiwać dla fali elektromagnetycznej innej dostępnej wielkości fizycznej, dzięki której możnaby dokładnie tak jak dla cząstek o masie spoczynkowej różnej od zera, także dla fotonu podać interpretację probabilistyczną. Okazało się, że [11,12,13,14,15] jako fotonowe funkcje falowe mogą służyć wektory Riemanna-Silbersteina (RS) zdefiniowane jako

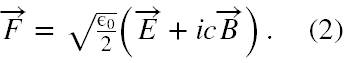
Jeżeli chodzi o opis samych fotonów ( tj. nieoddziałujących z materią ), to użycie wektora F ma wiele zalet w porównaniu do wykorzystania wektora A. A oto te zalety.

1) Równania Maxwella redukują się dla wektora F do jednej pary zespolonych równań postaci

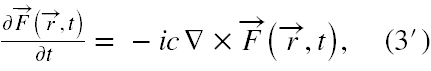
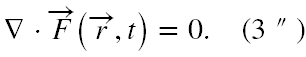
2) Podstawowe wielkości mechaniczne związane z fala elektromagnetyczną wyrażają się tylko poprzez samo F, tj.

a) całkowita energia

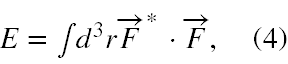
b) całkowity pęd

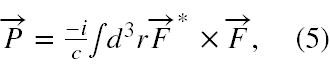
c) całkowity moment pędu

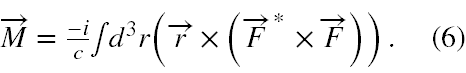
Wszystkie one wyglądają bardzo podobnie do kwantowomechanicznych wartości oczekiwanych.

Powstaje teraz zagadnienie jak rozwiązać równania Maxwella podane w formie (3), czyli odpowiedzieć na pytanie jakie są dopuszczalne postacie funkcjonalne pola wektorowego F(r,t)?

Odpowiedź jest znana od dawna, można ją znaleźć w [13], a także tam są wskazane dalsze odnośniki do pionierskich prac wprowadzających opis fal elektromagnetycznych przy użyciu wektora Riemanna-Silbersteina. W tym artykule zacytuję tylko te elementy, które są mi potrzebne do dalszych rozważań.

Aby znaleźć rozwiązania na wektor RS F(r,t) wygodnie jest przedstawić ten wektor jako wynik działania operatorów różniczkowych na zespolone pole wektorowe Z(r,t) będące zespoloną wersją potencjału Hertza, czyli

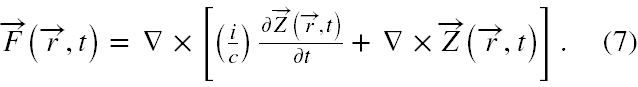
Postąpmy teraz za [21] i podziałajmy na obie strony (7) operatorem

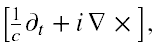
na mocy (3’) lewa strona tak otrzymanego równania jest równa 0. Natomiast druga strona po przekształceniu prowadzi do równania falowego d’Alemberta dla rotacji pola Z(r,t)

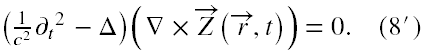
Dalsza treść [21] jest trochę niejasna, lecz posłużenie się [22] wyjaśnia, że korzystając z przemienności operatora d’Alemberta i operatora rotacji dochodzimy do wniosku, że każde pole Z(r,t) spełniające równanie falowe w formie (8") spełnia poprzez (7) równania Maxwella w postaci (3),

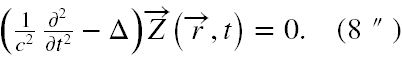
Należy pamiętać jednak, że z tego, iż Z(r,t) spełnia równianie (8") wynika tylko, że jest spełnione równanie falowe d’Alemberta dla rotacji tego pola, ale to nie oznacza, że każde rozwiązanie (8') spełnia równanie (8"). Dzieje się tak tylko dla tego szczególnego rozwiązania. Autorzy prac [21,22] wcale nie poszukują wszystkich rozwiązań równania (8'), a zadowalają się tym szczególnym rozwiązaniem.

Skoro zespolony potencjał Hertza Z(r,t) spełnia równanie (8"), to jego ogólne rozwiązanie ma postać rozwinięcia na fale płaskie w formie

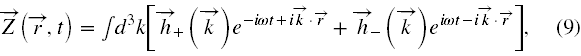
gdzie h±(k) to dowolne funkcje wektorowe wektora falowego k.

Stąd część pola F(r,t) o np. dodatnich częstościach może być zapisana jako

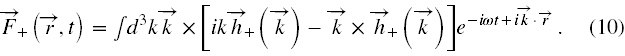
Funkcje h±(k), jak wynika z cytowanej literatury, mogą mieć różne postacie prowadzące do wiązek nazywanych jako wiązki Bessela, Laguerre’a-Gaussa, Hermite’a-Gaussa, eksponencjalnych lub jakiś innych pozwalających na lepszą konkretyzację cech fotonu albo też po zastąpieniu ich operatorami o odpowiednich regułach komutacji prowadzić do kwantyzacji pola elektromagnetycznego.

§4. Związek potencjału wektorowego A z potencjałem Hertza Z.

Przypomnijmy podstawowe fakty o potencjale wektorowym A(r,t). Jak podaję w uzupełnieniu B, wprowadzając cechowanie Lorentza możemy otrzymać równania falowe na A(r,t) i Φ(r,t) całkowicie równoważne równaniom Maxwella. Jednak w praktycznym opisie pól elektromagnetycznych oddziałujących z materią na ogół korzysta się z cechowania Coulomba. Z [20] można się dowiedzieć, że podczas kwantowania pola elektromagnetycznego okazuje się, iż część podłużna A oraz Φ nie są w rzeczywistości dynamicznymi stopniami swobody. Pozbywamy się ich poprzez odpowiednią transformację cechowania i otrzymujemy cechowanie promieniowania (Coulomba)

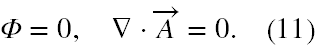
Oczywiście Φ = 0, jeżeli brak jest ładunków elektrycznych. W przeciwnym przypadku potencjał skalarny będzie spełniał równanie Poissona. Tak czy inaczej, pole promieniowania oddziałujące z materią opisuje tylko potencjał wektorowy spełniający równanie falowe oraz warunek cechowania Coulomba.

Aby obliczyć A(r,t) na podstawie znalezionego rozwiązania dla Z(r,t) (wzór 9), to z [22] wynika, że

Z(r,t) = Π_e(r,t) + iΠ_m(r,t) , (12)

oraz

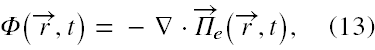
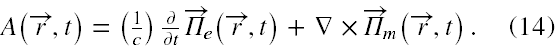
Tym samym z uwagi na fakt, że funkcje h±(k) nie zależą ani od czasu, ani od zmiennych przestrzennych potencjał wektorowy A(r,t) też będzie od nich zależał. Było dla mnie dużym zaskoczeniem, że funkcje te, to dowolne funkcje wektora k. Dla porównania zajrzyjmy do cytowanych przeze mnie monografii, a przekonamy się, że podane tam rozwiązania na A(r,t), takie które są najczęściej w nich dyskutowane, zawierają jako funkcje rozwinięcia tylko jakieś stałe wektory, których moduły zawsze można unormować do stałej 1.

Ten dziwny fakt może mieć tylko jedno wyjaśnienie. Aby nie „mącić“ studentom w głowach, w programach nauczania przeznaczonych dla wyższych uczelni powszechnie zataja się fakt, że potencjał wektorowy spełniający równanie falowe, dokładnie tak jak pole Z(r,t) posiada rozwinięcie ogólnego rozwiązania takie, w którym analogiczne do h±(k) amplitudy tego rozwinięcia są dowolnymi funkcjami k.

W ten sposób powinno być jasne, że zarówno A(r,t), jak i Z(r,t) spełniające to samo równanie falowe są rozwiązaniami dającymi pola E(r,t) i B(r,t) spełniającymi równania Maxwella w próżni.

UZUPEŁNIENIE A

Z uwagi na oszczędność tekstu użyłem gotowych oznaczeń z prac i podręczników. Dlatego czytając to uzupełnienie proszę zajrzeć do [8] i [24], gdzie jest wyjaśnienie symboliki, gdyby ktoś używał innych oznaczeń niż moje.

Rozwiązanie Wołkowa równania Diraca dla elektronu (E>0) i polaryzacji +1/2 wpadającego w pole fali płaskiej A^μ(φ) ma postać

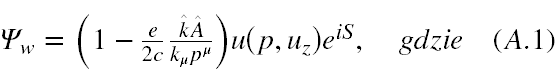
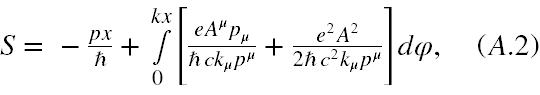
i użyłem oznaczenia u(p,u_z) = w¹(p), wzór (3.16) za [24].

Interpretacja rozwiązania Wołkowa podana w [8] głosi, że zakłada się w celu wyjaśnienia co to za stały bispinor u(p,u_z) znajduje się w tym rozwiązaniu, iż fala elektromagnetyczna, w której znajduje się elektron ma dowolnie małe wygasanie. Wówczas gdy x->∞, A->0 i Ψ_w powinna przechodzić w rozwiązanie równania Diraca dla cząstki swobodnej. Okazuje się [8], że u(p,u_z) pokrywa się z bispinorową amplitudą swobodnej fali płaskiej. Tak więc nie ma przeszkód, aby dla naszych celów i wygody przyjąć postać u(p,u_z) zgodnie ze wzorem (3.16) w [24], pozostaje jedynie do uzgodnienia kwestia jego unormowania.

Naszym celem jest pokazanie, że Ψ_w zawiera w sobie nie tylko stan w¹ (p), jaki posiadał elektron, gdy wpadał w pole fali płaskiej ale, że jest kombinacją liniową wszystkich swobodnych spinorów Diraca wⁱ(p), gdzie i = 1,...,4. Najłatwiej będzie to wykazać używając operatorów rzutowych na stany o określonym znaku energii i polaryzacji. Zauważmy, że elektron opisany rozwiązaniem Wołkowa na ogół nie znajduje się w spoczynku. A zatem będziemy musieli użyć ogólnych operatorów rzutowych.

Operator rzutowy na stan o określonym znaku energii dla cząstki Diraca o dowolnym pędzie ma postać

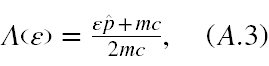
gdzie ε = ±1 i indeksuje znak energii. Natomiast operator rzutowy na stan o określonej polaryzacji dla cząstki Diraca ma postać

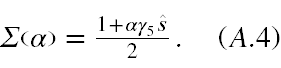
Parametr α = ±1 służy do uzyskiwania dwóch przeciwnych polaryzacji. Wektory pędu i polaryzacji muszą spełniać warunek s^μp_μ = 0.

Tak więc poddajmy Ψ_w działaniu iloczynu operatorów Λ(ε)Σ(α) i (pomijając rachunki) otrzymamy następujący wynik

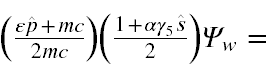
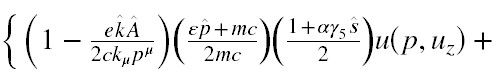
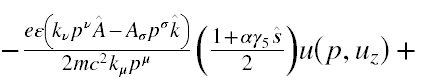
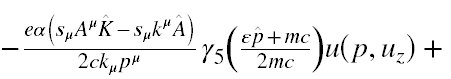
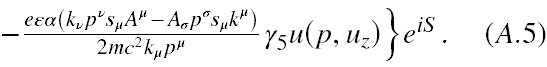
Wykonując rachunki oczywiście pominąłem eksponent, ponieważ jego wykładnik nie zawiera macierzy γ^μ, a tylko liczby i dlatego jest z nimi przemienny.

Teraz zwróćmy uwagę, że stan u(p,u_z) pod działaniem Λ(ε)Σ(α) tylko dla ε=1 i  α=1 przechodzi w siebie, a w pozostałych przypadkach daje 0. Jednak dla operatorów działających pojedynczo stan ten przechodzi sam w siebie również dla Λ(1) lub Σ(1). Na koniec zwróćmy uwagę, że we wzorze (A.5) jest człon zawierający u(p,u_z), na który nie działa jakikolwiek operator rzutowy. A zatem dla każdej kombinacji wartości parametrów ε i α wyrażenie (A.5) będzie zawierało niezerowe składowe.

Stan Ψ_w można rozłożyć używając operatorów rzutowych według następującej sztuczki wynikającej wprost z ich właściwości

Ψ_w = 1 · 1 · Ψ_w = {Λ(+1) + Λ(-1)}{Σ(-1) + Σ(+1)}Ψ_w
   = Λ(+1)Σ(+1)Ψ_w + Λ(+1)Σ(-1)Ψ_w + Λ(-1)Σ(+1)Ψ_w + Λ(-1)Σ(-1)Ψ_w

Zatem w oparciu o powyższą dyskusję dotyczącą działania operatorów rzutowych na Ψ_w widzimy, że rozwiązanie Wołkowa równania Diraca dla elektronu w polu płaskiej fali elektromagnetycznej jest kombinacją liniową wszystkich stanów elektronowych i pozytonowych.

UZUPEŁNIENIE B

Przypomnijmy wyprowadzenie równania falowego na A(r,t) idąc za [18,19]. Zakładamy, że opisywana przez Nas fala elektromagnetyczna rozchodzi się w próżni oraz brak jest ładunków elektrycznych i prądów. Zatem równania Maxwella w układzie SI przyjmują postać

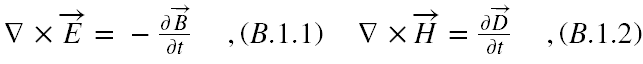
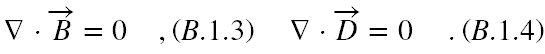
(W powyższych wzorach, jak i we wszystkich poniższych stosuję dla ułatwienia konwencję zapisu, że operator nabla jest wektorem i zawiera już w sobie strzałkę, jako jego symbol. Nie ma zatem potrzeby jej we wzorach dodatkowo wrysowywać.)

Ponieważ równość (B.1.3) zachodzi dla dowolnych pól zmiennych w czasie, więc pole B możemy wyprowadzić z potencjału wektorowego A

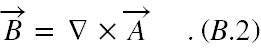
Równanie (B.2) możemy wstawić do (B.1.1) po prawej stronie za B, przenieść całość na lewą stronę i wyciągnąć przed nawias rotację i otrzymamy

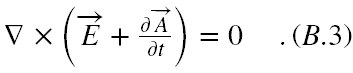
Oznacza to, że zawarta w nawiasie w (B.3) wielkość, której rotacja znika, może być przedstawiona jako gradient funkcji skalarnej, nazywanej potencjałem skalarnym Φ:

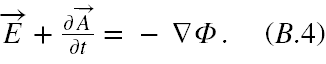
Możemy użyć (B.4) jako źródła definicji na E obliczanego z potencjałów A i Φ pamiętając, że Φ pokrywa się z potencjałem elektrostatycznym tylko w polu niezależnym od czasu. Zatem możemy zdefiniować E jako

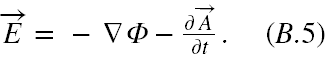
Zajmijmy się teraz drugą parą równań (B.1). Mnożymy stronami (B.5) przez ε₀, aby otrzymać określenie na D, a dzieląc (B.2) stronami przez μ₀ otrzymujemy określenie na H .

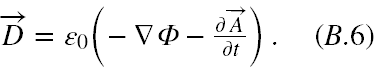
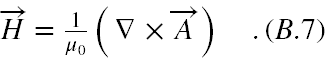
Dalej wstawiamy (B.6) i (B.7) do równań (B.1.2) i (B.1.4). Jeszcze mnożymy (B.1.2) stronami przez μ₀ i otrzymujemy z (B.1.2)

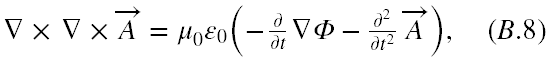
a z (B.1.4), po skróceniu stronami ε₀

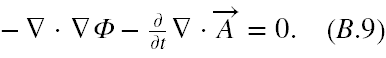
Równanie (B.8) musimy poddać przekształceniu korzystając z równości μ₀ε₀ = 1/c² oraz ze znanej tożsamości

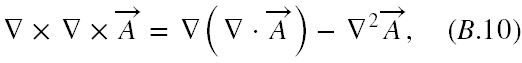
co w końcu daje

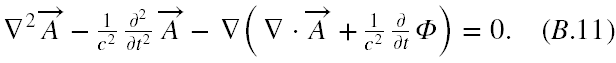
W ten sposób zastąpiliśmy układ czterech równań Maxwella dwoma równaniami, które są nadal ze sobą powiązane. Aby je rozseparować musimy wykorzystać dowolność wyboru potencjałów, która wynika ze sposobu ich zdefiniowania.

Zauważmy, że skoro B(r,t) jest określone jako rotacja A(r,t), więc dodając do A(r,t) gradient dowolnej funkcji skalarnej nie zmieniamy pola magnetycznego. A zatem fizycznie są dozwolone dowolne transformacje cechowania A(r,t) postaci

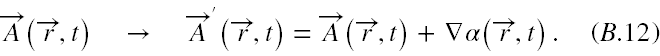
Jednak pole E(r,t) też zależy od A(r,t). Aby transformacja cechowania potencjału A(r,t) nie zmieniała i tego pola musimy jednocześnie z A(r,t) poddać transformacji również potencjał skalarny Φ(r,t). Żeby obliczyć jego transformację podstawmy w (B.5) A'(r,t) za A(r,t), potem pochodną po czasie z α(r,t) wciągnijmy pod pierwszy gradient i mamy

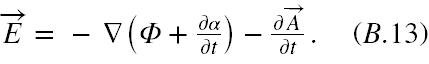
Jeżeli teraz dokonamy transformacji cechowania Φ w (B.13) w formie

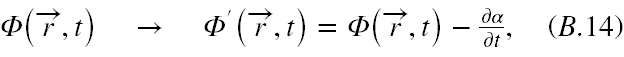
to pole elektryczne również pozostaje bez zmiany.

Wprowadziwszy pojęcie transformacji cechowania dla potencjałów przyjrzyjmy się wzorowi (B.11). Zwróćmy uwagę na zawartość nawiasu stojącego pod znakiem gradientu. Jeżeli przyrównać ją do zera, to równanie (B.11) stanie się równaniem d’Alemberta (falowym) na potencjał wektorowy. Otrzymaną równość

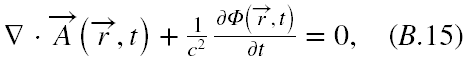
nazywamy warunkiem Lorentza na potencjały. Wyliczając z tego warunku dywergencję A(r,t) i wstawiając jej wartość do (B.9) otrzymamy podobne równanie falowe na potencjał skalarny. Tak więc widać, że równania falowe na oba potencjały będą równoważne równaniom Maxwella, jeżeli warunek Lorentza też będzie niezmienniczy względem transformacji cechowania.

Zatem poddajmy równanie (B.11) transformacji cechowania (oczywiście cechujemy oba potencjały) i mamy

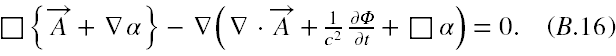
Widać z powyższego, że po uwzględnieniu warunku Lorentza dla nieprzecechowanych potencjałów ponownie otrzymamy równanie falowe dla potencjału A'(r,t), jeżeli funkcja α(r,t) będzie spełniać równanie d’Alemberta. Wtedy też będzie spełniony warunek Lorentza dla przecechowanych potencjałów, czyli będzie się zerować zawartość drugiego nawiasu stojącego w (B.16) pod znakiem gradientu. Jak można się przekonać z [23] jest wiele funkcji skalarnych spełniających równanie falowe d’Alemberta. W tej sytuacji również równanie (B.9) będzie spełnione dla przecechowanych potencjałów.

Zatem mamy udowodnione, że zamiast rozwiązywać równania Maxwella można rozwiązać prostsze równania falowe na potencjały A(r,t) i Φ(r,t), a następnie z (B.2) i (B.5) policzyć pola E(r,t) i B(r,t).

¹  Osoby, które nie znają dobrze mechaniki kwantowej, a raczej tylko jej podstawy powinny się zdziwić w tym miejscu, bo jak tu uwzględnić na przykład zjawiska Zeemana i Starka? Zjawiska te zależą przecież od pól magnetycznego i elektrycznego. Ograniczając się do równania Schrödingera rzeczywiście tak jest.

Gdy przechodzimy do równania Diraca, to jego rozwiązaniem jest funkcja falowa będąca czterowektorem (bez zagłębiania się w szczegóły), której składowe są wzajemnie sprzężone. Rozwikłanie ich prowadzi do równania drugiego rzędu, gdzie pojawiają się człony zależne już od samych pól [25]. I tak pole magnetyczne sprzęga się z operatorem spinu, natomiast pole elektryczne z macierzą α.

Jeżeli ograniczamy się do zagadnienia nierelatywistycznego, które występuje na przykład w lekkich atomach, to równanie Diraca jest dla równania Schrödingera źródłem szeregu poprawek, oprócz wspomnianego wyżej sprzężenia z polem magnetycznym, także niezależnych od spinu, czego przykładem jest poprawka - zwana członem Darwina - proporcjonalna do ∇⋅E. Ponieważ dywergencja pola elektrycznego jest równa 0 wszędzie tam, gdzie nie ma ładunku, więc jest różna od zera dla atomów, tylko w ich jądrach.

Bibliografia

[1] J. D. Bjorken, S. D. Drell, Relatywistyczna Teoria Kwantów, PWN, Warszawa 1985, §§7.6-7.8;

[2] A. S. Dawydow, Mechanika Kwantowa, PWN, Warszawa 1969, wzór 78.2;

[3] W. B. Bierestecki, E.M.Lifszyc, L. P. Pitajewski, Relatywistyczna Teoria Kwantów, Tom I, PWN, Warszawa 1972, wzór (43.9);

[4] S. Weinberg, Teoria Pól Kwantowych, Tom I, PWN, Warszawa 1999, wzór (8.4.15);

[5] Dirac P. A. M., The quantum theory of the emission and absorption of radiation, Proc.Roy.Soc. London, A 114, 243,(1927);

[6] J. Petykiewicz, Optyka Falowa, PWN, Warszawa 1986;

[7] R. Glauber, Stulecie Kwantów Światła, Postępy Fizyki, 58,14(2007);

[8] D, M, Volkov, Z. Phys. 94, 250(1935); W. B. Bierestecki, E.M.Lifszyc, L. P. Pitajewski, Relatywistyczna Teoria Kwantów, Tom I, PWN,Warszawa 1972, §40;

[9] A. I. Nikiszow. W. I. Ritus, ŻETF 46, 776(1964); W. B. Bierestecki, E.M.Lifszyc, L. P. Pitajewski, Relatywistyczna Teoria Kwantów, Tom I, PWN,Warszawa 1972, §98;

[10] W. Wasilewski, P. Kolenderski, R. Frankowski, Spectral Density Matrix of a Single Photon Measured , Phys.Rev.Lett. 99, 123601(2007);

[11] I. Białynicki-Birula, Z. Białynicka-Birula, Beams of electromagnetic radiation carrying angular momentum:The Riemann-Silberstein vector and the classical-quantum correspondence,Optics Communications 264, 342(2006);

[12] I. Białynicki-Birula, Z. Białynicka-Birula, Exponential beams of electromagnetic radiation, J.Phys. B: At.Mol.Opt.Phys. 39, S545-S553 (2006);

[13] I. Białynicki-Birula, Exponential Localization of Photons, Phys.Rev.Lett. 80, 5247(1998);

[14] J. E. Sipe, Photon wave functions, Physicsl Review A, 52, 1875(1995);

[15] B. J. Smith, M. G. Raymer, Photon wave functions, wave-packet quantization of light, and coherence theory, New Journal of Physics 9,414(2007);

[16] C. C. Gerry, P. L. Knight, Wstęp Do Optyki Kwantowej, PWN, Warszawa (2007), §3.1. ;

[17] W. Gawlik, Elektrodynamika Atomu we Wnęce Rezonansowej, Postępy Fizyki, 42,33(1991);

[18] M. Suffczyński, Elektrodynamika, PWN, Warszawa (1980);

[19] J. D. Jackson, Elektrodynamika klasyczna, PWN, Warszawa (1982);

[20] J. D. Bjorken, S. D. Drell, Relatywistyczna Teoria Kwantów, PWN, Warszawa 1985, §14.2;

[21] I. Białynicki-Birula, Z. Białynicka-Birula, The role of the Riemann–Silberstein vector in classical and quantum theories of electromagnetism, J. Phys. A 46, 053001 (2013);

[22] A. Nisbet, Hertzian electromagnetic potentials and associated gauge transformations, Proc. R. Soc. A 231, 250 (1955);

[23] R. S. Ingarden, Elektrodynamika Klasyczna i Kwantowa, Uniwersytet Mikołaja Kopernika - Skrypty i teksty pomocnicze, Toruń 1976, §9;

[24] J. D. Bjorken, S. D. Drell, Relatywistyczna Teoria Kwantów, PWN, Warszawa 1985,§2.1, §§3.1-3.2;

[25] W. B. Bierestecki, E.M.Lifszyc, L. P. Pitajewski, Relatywistyczna Teoria Kwantów, Tom I, PWN,Warszawa 1972,§§32-34; J. D. Bjorken, S. D. Drell, Relatywistyczna Teoria Kwantów, PWN, Warszawa 1985, §4.3;