W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 9

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: sobota, 24, październik 2015 13:55

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 1.66, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki" , WSiP , Warszawa 1976

Udowodnić, że w ruchu jednostajnie przyspieszonym bez prędkości początkowej droga przebyta przez ciało w trzynastej sekundzie ruchu jest równa drodze przebytej przez to ciało w ciągu pierwszych pięciu sekund niezależnie od wartości przyspieszenia.

Zadanie nr 1.16, M.S.Cedrik i inni - "Zadania z fizyki", PWN, Białystok 1975

Ciało, poruszając się ze stałym przyspieszeniem, przebywa kolejno dwa odcinki drogi s = 15 m odpowiednio w ciągu t ₁ = 2 s, i t ₂ = 1 s. Znaleźć przyspieszenie i szybkość ciała na początku pierwszego odcinka drogi.

Rozwiązanie

zadanie nr 1.66 

W zadaniu mamy powiedziane, że ciało porusza się ruchem jednostajnie przyspieszonym, przy czym jego prędkość początkowa jest równa zero. Zatem ma zastosowanie wzór na drogę postaci

s = a(Δt)²/2.

Droga przebyta w ciągu pierwszych pięciu sekund, to

s (Δt = 5s) = (a/2)25s².

Jeśli chodzi o drogę przebytą w ciągu trzynastej sekundy, to nie ma na to bezpośredniego wzoru! Po prostu trzeba od drogi przebytej w ciągu trzynastu sekund odjąć drogę przebytą w ciągu pierwszych dwunastu sekund, czyli

s(13) = s(Δt =13s) - s(Δt =12s) = (a/2)(13s)² - (a/2)(12s)²

= (a/2)(169s² -144s²) = (a/2)25s².

Co czyni tezę oczywistą!

zadanie nr 1.16 

To zadanie również jest poświęcone prostoliniowemu ruchowi jednostajnie przyspieszonemu, w którym tym razem jest pytanie o prędkość początkową i przyspieszenie. Dlatego wypiszmy najbardziej ogólny wzór na drogę w tym ruchu

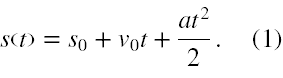
Skoro w zadaniu nie ma pytania o położenie ciała na początku ruchu, zatem należy przyjąć, że s ₀ = 0. Zastosujmy stąd równanie (1), stosując oznaczenia danych użyte w tym zadaniu, do drogi przebytej przez ciało w ciągu czasu t ₁

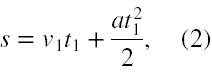
oraz, dla wygody obliczeń, dla drogi przebytej w ciągu czasu t ₁+t ₂

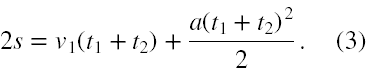
Równania (2) i (3) zawierają dwie zmienne niewiadome v ₁ oraz a, zatem jest szansa, że układ może być oznaczony. Współczynniki przy zmiennych niewiadomych, to wyrażenia algebraiczne, a nie liczby. Stąd stosowanie elementarnych metod rozwiązywania układu dwóch równań z dwiema niewiadomymi w tym przypadku jest niewygodne. Dlatego zastosujemy metodę wyznaczników (¹). Jej opis na poziomie elementarnym, czyli układu 2 równań z 2 niewiadomymi można znaleźć w [1], a dla przypadku ogólnego np. w [2].

Rozwiązywanie układu (2-3) należy rozpocząć od zbadania, czy układ jest układem Cramera. W tym celu w układzie (2-3) zamieńmy strony równań rolami (czyli na lewą stronę przenieśmy prawą i na odwrót) i wypiszmy macierz główną tego układu traktując, że v ₁ jest pierwszą niewiadomą, a a drugą. Stąd otrzymujemy

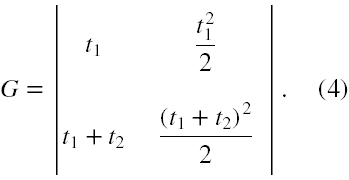
Wyznacznik tej macierzy jest równy (²)

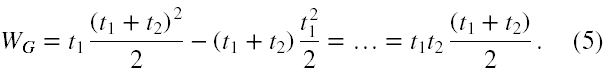
Ponieważ zmienne t ₁ i t ₂ są dodatnie, więc wyznacznik W_G jest różny od zera, a zatem układ (2-3) ma dokładnie jedno rozwiązanie.

Aby obliczyć przyspieszenie potrzebna jest nam macierz przyspieszenia, która powstaje z (4) poprzez zastąpienie kolumny współczynników zmiennej a wyrazami 'wolnymi', czyli poprzez drogi 's' i '2s'

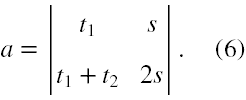
Wyznacznik tej macierzy jest równy W_a = t ₁·2s - s(t ₁ + t ₂) = s(t ₁ - t ₂). Zatem przyspieszenie możemy już obliczyć, które jest dane jako następujący iloraz

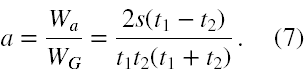
Aby obliczyć prędkość potrzebna jest nam macierz prędkości, która powstaje z (4) poprzez zastąpienie kolumny współczynników zmiennej v ₁ wyrazami 'wolnymi', czyli poprzez drogi 's' i '2s'

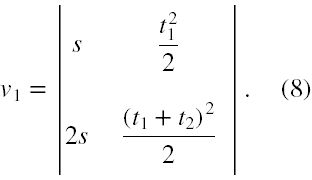
Wyznacznik tej macierzy jest równy

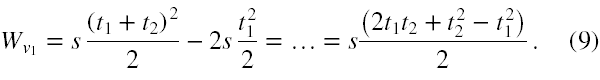
Stąd prędkość początkowa w tym ruchu jest równa

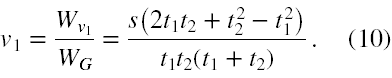
(¹) Bez użycia metody wyznaczników najłatwiej uzyskać rozwiązanie mnożąc równanie (2) stronami przez -(t ₁ + t ₂), a (3) stronami przez +t ₁. Wtedy dodając stronami równania zredukują się wyrazy zawierające niewiadomą v ₁. Z tak powstałego równania można już wyznaczyć niewiadomą a. Podstawiając wyliczone a do jednego z równań (2-3) wyliczymy v ₁.

(²) Wyznacznik każdej macierzy o wymiarach 2x2 postaci

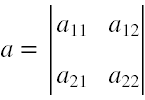
jest równy W_a = a₁₁a₂₂ - a₂₁a₁₂.

LITERATURA

[1] W. Leksiński, B. Macukow, W. Żakowski Matematyka w zadaniach, część 1, rozdział 2, WNT, Warszawa 1972.

[2] A. Mostowski, M. Stark, Elementy algebry wyższej, rozdział IV, PWN, Warszawa 1977.