Quasi-klasyczna interpretacja rozwiązań równania Diraca w jednorodnym polu elektrycznym

Szczegóły

Kategoria: Równanie Diraca

Opublikowano: czwartek, 25, luty 2016 16:03

Autor : Janusz Szcząchor

Quasi-classical interpretation of some solutions of the Dirac equation in a homogeneous electric field

Abstract: Formulas of energy and momentum for a Dirac particle in a homogeneous electric field are analysed. To obtain explicit values of them the supplementary interpretation of the wave function is used. The probability of transmitting electrons through a homogeneous electric field barrier is calculated to be one.

§1. Wstęp

A zatem przystępujemy do interpretacji otrzymanych w [1] rozwiązań równania Diraca w jednorodnym polu elektrycznym. Najpierw potraktujemy funkcje z + ct + D oraz z - ct + D jako sumaryczne zmienne i dla nich będziemy przeprowadzać analizę otrzymanych wyników.

Potem będziemy zastanawiać czy mogą mieć sens jakieś konkretne zależności między z i ct oraz D. Niestety, jakiekolwiek tego typu zależności będą łamać symetrię równania Diraca w jednorodnym polu elektrycznym, gdzie są dopuszczalne wartości rozwiązań równania Diraca dla dowolnych z i ct.

Jednak należy tu zauważyć, że w przeciwieństwie do typowych rozważanych akademicko problemów kwantowych, w których mechanika kwantowa daje jednoznaczne rozwiązania, to w tym przypadku ona nie daje i po prostu nie może dać jednoznacznych rozwiązań. Stąd otrzymane dzięki niej wyniki muszą zostać ograniczone do tych, które są fizycznie poprawne. Będzie to z pewnością zaskoczenie dla wielu osób, że są problemy na poziomie mikroskopowym, które mechanika kwantowa nie potrafi do końca rozwiązać i nie z przyczyn rachunkowych, a fundamentalnych.

Ponadto pracę tę traktuję jako okazję do postawienia pytań i hipotez co do tego co jest faktycznie rozwiązaniem tego problemu oraz jako zachętę do ogólnej dyskusji w tym temacie.

§2. Energia i pęd cząstki Diraca w jednorodnym polu elektrycznym

W pierwszym rzędzie przeanalizujemy otrzymane wzory na energię i pęd, czyli wzory (30), (31), (36) i (37) w [1]. Jeśli chodzi o energię, to obydwa otrzymane wzory można wyrazić w jednolity sposób w formie

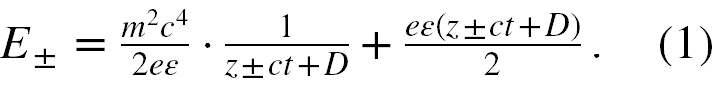
Potraktujmy zmienną z ± ct + D jako sumaryczną zmienną i oznaczmy ją przez x. Jeżeli oznaczymy jako α stałą m²c⁴/2eε, a jako β stałą eε/2, to wzór (1) można napisać w formie

E(x) = α/x + βx . (2)

Najpierw połóżmy obie stałe jako równe 1 i przeanalizujmy zachowanie funkcji 1/x + x przy pomocy programu do sporządzania wykresów funkcji (http://localhost/polish
/wykresy_funkcji.php). Otrzymamy poniższy wykres - patrz rysunek nr 1.

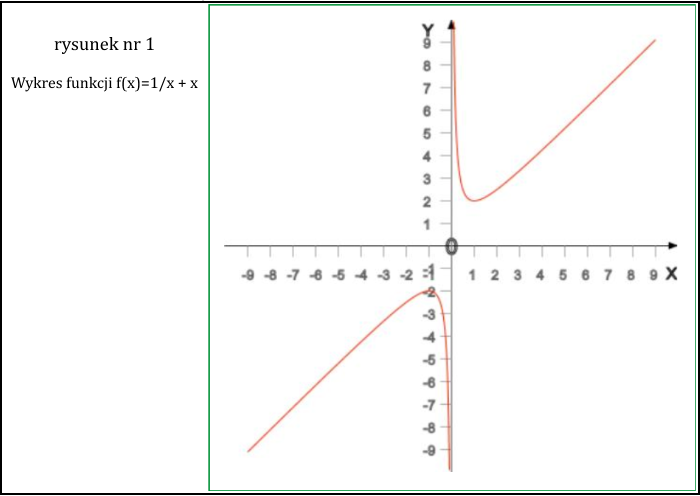
Jak widać składa się on z dwóch części, przedzielonych asymptotą pionową dla x = 0. W części pierwszej dla zmiennej x o wartościach ujemnych wartość energii cząstki jest ujemna i posiada maksimum zupełnie tak jak powinno być dla rozwiązań o energii ujemnej, natomiast w części drugiej dla x o wartościach dodatnich energia jest dodatnia i posiada minimum zupełnie tak jak powinno być dla rozwiązań o energii dodatniej.

Skoro mamy komputerowy wykres funkcji, więc nie ma potrzeby robić całego badania tej funkcji. Policzymy jedynie ile dokładnie wynoszą owe maksimum i minimum, czy są równe tyle ile powinno być według teorii Diraca?

Przyrównajmy zatem pierwszą pochodną po x funkcji E(x) do zera i mamy

dE(x)/dx = - α/x² + β = 0. (3)

Rozwiązaniem jest wartość x = ± mc²/eε. Druga pochodna d²E(x)/dx² = 2α/x³. Zatem zbadajmy znak drugiej pochodnej dla tych punktów. Dla x = - mc²/eε druga pochodna jest ujemna, zatem w tym punkcie mamy maksimum i jest ono równe

E(- mc²/eε) = - mc² , (4)

a dla drugiego druga pochodna jest dodatnia, a stąd mamy tu minimum równe

E(mc²/eε) = mc² . (5)

Podsumowując możemy podejrzewać, że dla x = z ± ct + D mających wartości dodatnie wzór (1) opisuje energię rozwiązań elektronowych, a dla wartości ujemnych rozwiązania antycząstkowe. Zróbmy to samo dla wzoru na pęd cząstki.

Wzory na pęd dla Ψ¹ i Ψ² różnią się nieco od siebie, stąd będą analizowane osobno. Najpierw weźmiemy wzór na pęd dla Ψ¹. Przypomnijmy go

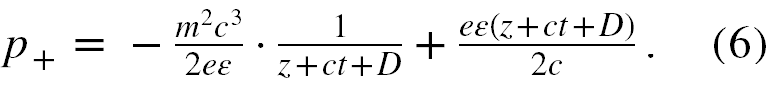
Potraktujmy zmienną z + ct + Djako sumaryczną zmienną i oznaczmy ją przez x . Jeżeli wprowadzimy ponownie stałe α i β równe jak wyżej , to wzór (6) można napisać w formie

P₊(x) = - α/cx + β/c . (7)

Kładąc stałe równe 1 otrzymujemy funkcję f(x) = - 1/x + x, której wykres jest poniżej, rysunek nr 2.

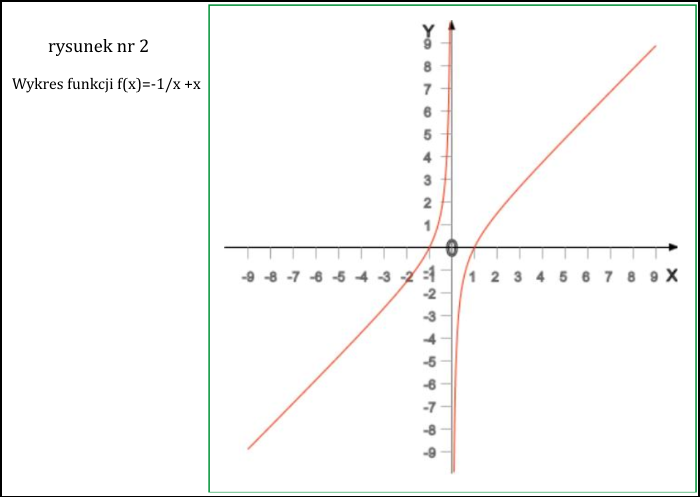
Jak widać funkcja ta ma maksima i minima w x = ±∞ oraz dla x → 0 zarówno z lewej, jak i z prawej strony. Jednak o wiele ciekawsze są miejsca zerowe, znajdziemy je. Rozwiązując równanie P₊(x) = 0 otrzymujemy ponownie, że te miejsca zerowe to x = ± mc²/eε. Należy dodatkowo zauważyć, że w punktach tych pęd zmienia zwrot.

Teraz weźmiemy wzór na pęd dla Ψ². Przypomnijmy również i jego

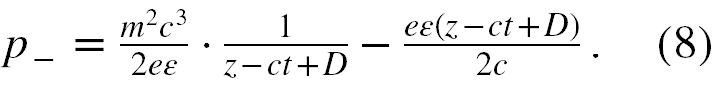
Z kolei potraktujmy zmienną z - ct + D jako sumaryczną zmienną i oznaczmy ją przez x. Jeżeli i teraz wprowadzimy ponownie stałe α i β równe jak wyżej, to wzór (8) można napisać w formie

P_-(x) = α/cx - β/c . (9)

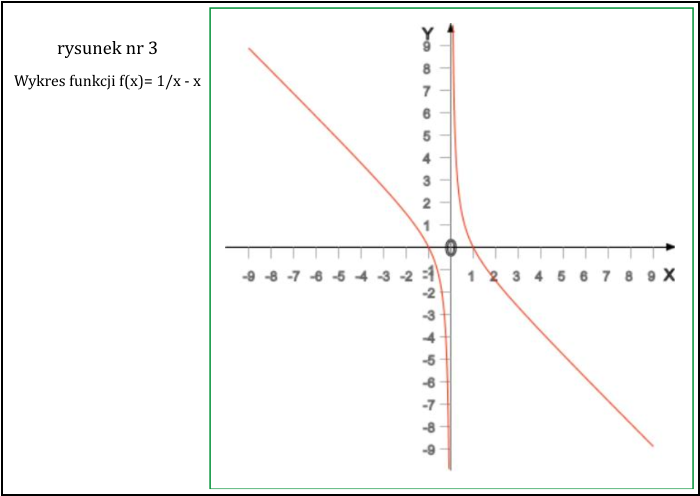
Ponownie kładąc stałe równe 1 otrzymujemy funkcję f(x) = 1/x - x, której wykres jest poniżej na rysunku nr 3. Jak widać funkcja ta również ma maksima i minima w x = ±∞ oraz dla x → 0 zarówno z lewej, jak i z prawej strony. Jeśli chodzi o miejsca zerowe, to są takie same. Rozwiązując równanie P _- (x) = 0 otrzymujemy również, że te miejsca zerowe to x = ± mc²/eε. Zauważmy, że w punktach tych pęd zmienia zwrot, ale w sposób przeciwny niż w poprzednim przypadku.

To już wszystko co możemy wyinterpretować z otrzymanych rozwiązań dla równania Diraca w jednorodnym polu elektrycznym bez łamania symetrii tego równania.

§3. Podejście quasi-klasyczne

Przyjrzyjmy się jeszcze raz otrzymanym wzorom (1), (6), (8) na energię i pęd. Widać z nich, że dla każdej pary wartości zmiennych (x,ct) otrzymujemy jakąś, na ogół inną wartość zmiennych E i p.

Jeżeli przypomnimy sobie jak to wygląda dla stanów stacjonarnych, to dla nich w danym stanie wartości E i p nie zależą od zmiennych (x,ct), są stałe dla każdej takiej pary. W takich też przypadkach stany niestacjonarne opisują tylko przejścia między takimi stanami stacjonarnymi, a więc nie zmieniają one braku zależności E i p od x i ct.

Jednak od strony doświadczalnej wiemy, że istnieje praktyczna realizacja jednorodnego pola elektrycznego, a jest nią generator elektrostatyczny [2,3]. Po dogłębnej analizie tej literatury dochodzi się do wniosku, że energia i pęd przyspieszanych w nim cząstek nie mogą przyjmować dowolnych wartości tak po prostu, ale w zasadzie stosują się do praw relatywistycznej mechaniki klasycznej.

Tu moja dygresja. Osobiście przypuszczam, że nie interesowano się zbytnio rozwiązaniami równań kwantowych typu jaki tu prezentuję, bo widać co do jednorodnego pola elektrycznego, to teoria oparta na mechanice klasycznej dobrze się sprawuje.

Z mechaniki klasycznej wiemy, że ładunki w polu elektrycznym poruszają się określonym torem, co oznacza, że pary dopuszczalnych wartości (x,ct) są ustawione w ciągi uszeregowane według wzrastającego czasu. Oznacza to też, że w rzeczywistości spośród wszystkich w (1), (6), (8) dopuszczalnych przez równanie Diraca wartości E i p, tylko niektóre z nich są faktycznie dopuszczalne w Przyrodzie i do tego jest między nimi określone następstwo czasowe.

Zatem już wiemy, że równanie Diraca nie jest w stanie prawidłowo opisać ruchu cząstki naładowanej w jednorodnym polu elektrycznym, dopuszcza zbyt wiele rozwiązań, jak i nie kreuje właściwego następstwa czasowego zdarzeń (należy tu dodać, że nie kreuje żadnego takiego następstwa). Oznacza to, że Przyroda realizuje złamaną symetrię równania Diraca.

I my też w tej chwili złamiemy tę symetrię wybierając tylko te punkty czasoprzestrzeni (x,ct) do analizy wzorów (1), (6), (8) na energię i pęd, które wybierają równania mechaniki klasycznej.

Zgodnie z relatywistyczną mechaniką klasyczną [4], ruch cząstki naładowanej w jednorodnym polu elektrycznym jest opisany II zasadą dynamiki Newtona w formie

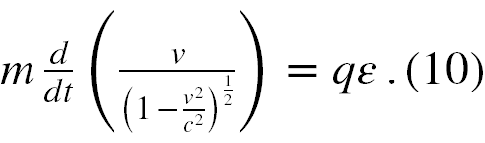
Biorąc pod uwagę, że rozwiązaliśmy równanie Diraca w polu potencjału A₀ = ε, gdzie pole elektryczne to −εk oraz oraz dla ładunku elektronu, czyli −e widzimy, że w Naszym przypadku siła przyspieszająca jest równa eεk, ładunek elektryczny porusza się w kierunku dodatnim na osi z. Zatem (10) poprawnie opisuje ruch naszego elektronu, jeżeli q = + |e|. Całkując to równanie otrzymujemy, że

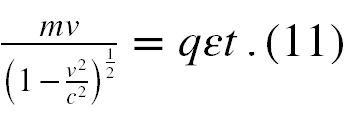
Z równania (11) z kolei wyliczamy, że prędkość cząstki w tym ruchu jest dana jako

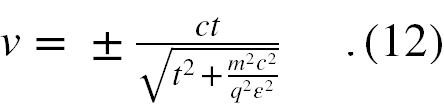
Skoro v = dz/dt, to możemy powyższe równanie potraktować jako równanie różniczkowe na z, a następnie całkując je metodą przez podstawienie otrzymamy, że położenie z i czas t są ze sobą powiązane w tym ruchu następującą relacją

gdzie C - to stała całkowania, a δ = mc²/eε, gdzie położyliśmy q = e i e > 0. Przy pomocy tej zależności będziemy analizować wzory (1), (6), (8) na energię i pęd.

a) ruch elektronu (rozwiązanie o dodatniej energii) w kierunku dodatnim osi z

Jak zakładaliśmy w [1] ( §2 Ruch ładunków w jednorodnym polu elektrycznym - patrz rysunek tamże ) wybrane przez Nas pole elektryczne przesuwa elektron w kierunku dodatnim osi z, a zależność z(t) jest dana wzorem (13). Bierzemy pod uwagę elektron o rzucie spinu w górę, czyli wzory na E i p dla tego przypadku, to te z sygnaturą ‘+’ spośród (1). (6), (8).

Teraz istotnym elementem rachunków jest dopasowanie w tych wzorach stałych C i D tak, aby otrzymać poprawne równanie równanie toru dla naszej cząstki oraz poprawne wartości E i p ( o ile okaże się to możliwe ).

Zakładamy, że w chwili t = 0 elektron znajduje się w położeniu z = 0, a następnie porusza się z dodatnim zwrotem na osi z. Analiza wzoru (13) pokazuje, że równanie ruchu tego elektronu musi mieć formę ( C = -δ )

z = −δ + (t²c² + δ²)^1/2, (14)

Bo tylko wtedy z(t = 0) = 0.

Teraz musimy uzgodnić wzory na E i p. Podstawiając wzór (14) do (1) w wersji z ‘+’, a potem do (6) widzimy, że dla punktu (z = 0, t = 0) musimy położyć D = δ. Wtedy zmienna z+ct+D przyjmie w tym punkcie wartość δ, bo dla niej E przyjmie pożądaną wartość mc², a p wartość 0. Dokładnie tak jak powinno być dla spoczywającego elektronu.

Z kolei spróbujmy wyrazić wzór na E₊ tylko przez zmienną z. W tym celu z (14) wyliczamy t. Będzie to

tc = ±{(z + δ)² − δ²}^1/2. (15)

Ponieważ dla elektronu o dodatniej energii czas płynie do przodu, więc wyrażenie z ‘+’ wstawiamy do wzoru na na E₊ w (1), doprowadzamy wzór do wspólnego mianownika i mamy

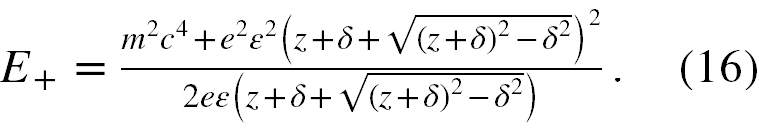
Podzielmy to równanie stronami przez e²ε², za m²c⁴/e²ε² podstawmy δ², rozwińmy kwadrat w liczniku, dokonajmy w liczniku redukcji wyrazów podobnych oraz wyłączmy wspólny czynnik przed nawias, skracamy licznik i mianownik przez 2(z+δ+√[(z+δ)²-δ²]) oraz mnożymy stronami przez e²ε². W końcu otrzymujemy, że

E₊ = mc² + eε. (17)

Jak widać jest to dokładnie wzór z relatywistycznej mechaniki klasycznej. Podobnie przeprowadzając takie obliczenia dla p₊ , ale w kierunku, aby wyrazić go jako funkcję tylko czasu otrzymamy, że

P₊ = eε. (18)

b) ruch elektronu ( rozwiązanie o ujemnej energii ) w kierunku ujemnym

Jak to wskazałem wcześniej, w szczególności na podstawie rysunku nr 1, rozwiązanie równania Diraca w jednorodnym polu elektrycznym dla rzutu spinu w górę dopuszcza sytuację, że energia elektronu może być ujemna. Aby jednak taka sytuacja była stała, zmienna z+ct+D musi przybierać stale wartości ujemne ( patrz wzór 1 ). W tym celu elektron nie tylko musi się poruszać w kierunku z -> -∞, ale także czas musi płynąć u niego wstecz. Wtedy rzeczywiście z równania (11) będzie wynikać, że pęd tej cząstki będzie ujemny.

Jednak elektron opisany rozwiązaniem o ujemnej energii powinien dynamiką ruchu nie różnić się od tegoż o dodatniej energii, wszak mają ten sam ładunek elektryczny. Co więcej jest on opisany tą samą funkcją falową. Jak widać równanie Diraca w takim polu ma problemy z opisem stanów o ujemnej energii.

Interesującym jest zauważenie, że jeżeli zmienimy zwrot pola elektrycznego na przeciwny i jednocześnie zmienimy też ładunek elektryczny na przeciwny, to otrzymamy to samo równanie Diraca co dotychczas, lecz będzie ono opisywać pozytony i to przy pomocy tej samej funkcji falowej i tych samych wzorów na energię i pęd.

Wyjaśnienie wydaje się być dość oczywiste. Równanie Diraca w jednorodnym polu elektrycznym nie generuje rozwiązań o ujemnej energii, które mogą służyć do opisu antycząstek, dlatego jest brak dodatkowych funkcji falowych. Zmiana znaku energii jest związana ze zmianą znaku pracy w polu elektrycznym. Wszak to praca nad pozytonem w polu elektrycznym jest dodatnia. Tym samym zmiany znaku energii dla ruchu cząstek Diraca w tym polu raczej nie mają nic wspólnego z opisem antycząstek.

§4. Prawdopodobieństwo przejścia elektronu przez barierę jednorodnego pola elektrycznego

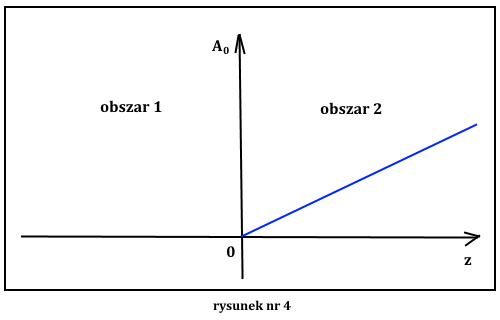
Spróbujemy teraz policzyć prawdopodobieństwo przejścia elektronu przez barierę jednorodnego pola elektrycznego, którego źródłem jest potencjał skalarny postaci φ = εz, gdzie ε, to pewna stała dodatnia, patrz rysunek nr 4.

W obszarze 1 elektron jest opisany bispinorem swobodnym w przedstawieniu spinorowym i o rzucie spinu w górę postaci [6]

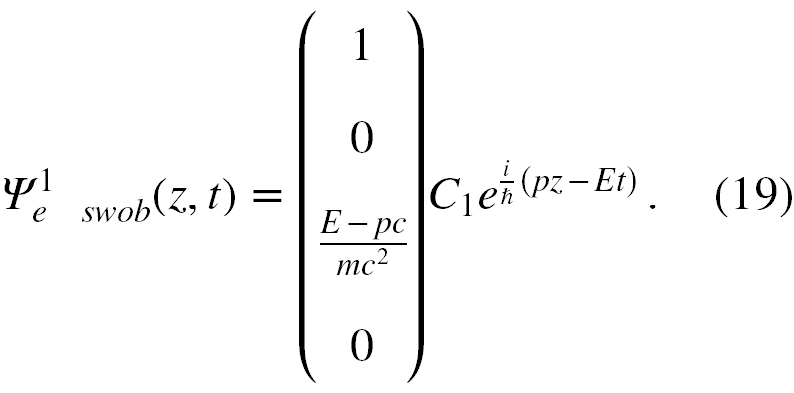
Tutaj E i p, to stałe. Elektron wpada w pole elektryczne w punkcie z = 0. Założymy dla wygody, że dzieje się to również w chwili t = 0. Wtedy w tym punkcie funkcja falowa składa się tylko z kolumny - czterowektora.

Spróbujemy teraz ją zszyć z rozwiązaniem dla jednorodnego pola elektrycznego w obszarze 2 postaci

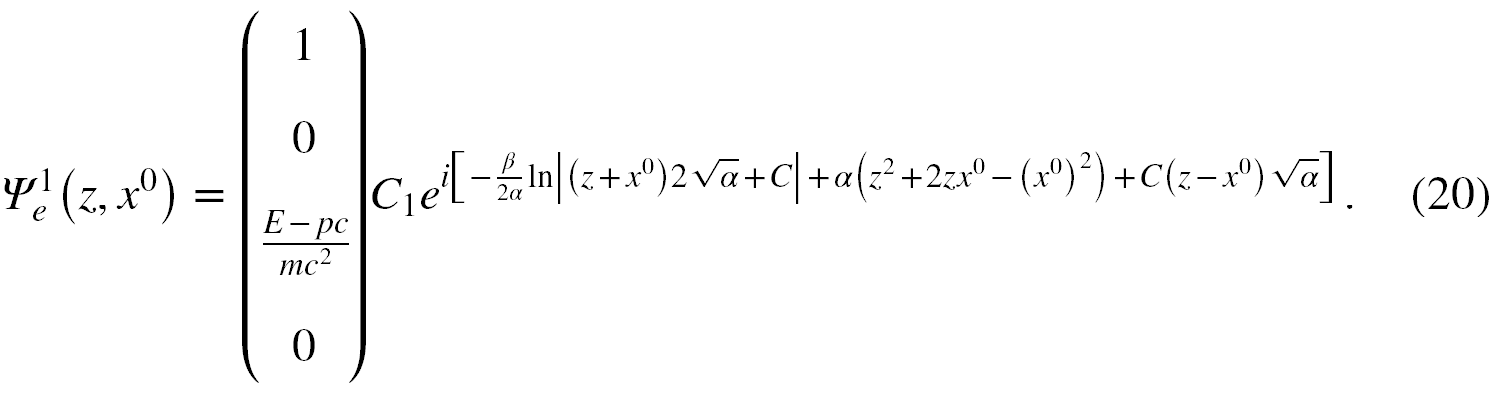
W nim E i p, to funkcje dane wzorami E₊ w (1) i p+ w (6). Ponieważ położyliśmy z = 0, jak i ct = 0, a funkcje te spełniają relację E² = p²c² + m²c⁴, więc manewrując wartością stałej D we wzorach na E₊ i p₊ możemy zrównać wartości tych funkcji w momencie wejścia elektronu w pole elektryczne, będące jednocześnie punktem zszycia obu bispinorów ze sobą, z wartościami stałych E i p w bispinorze swobodnym.

W takim punkcie zszycia wykładnik czynnika fazowego w (20) będzie zawierał wyłącznie stałą postaci -iβln|C|/2α. Stała C jest powiązana ze stałą D relacją [1] D = C/2√α. Wybierając stałą C₁ jako eksponent z wykładnikiem iβln|C|/2α zamieniamy czynnik fazowy bispinora (20) w 1.

Podobnie kładąc C₁ we wzorze (19), to zupełnie inna stała od poprzedniego C₁, jako równą 1 zszywamy oba bispinory w punkcie z = 0, ct = 0 ze sobą w ten sposób, że stają się identyczne. Tym samym prąd prawdopodobieństwa, dany wzorem j_z = cΨ†α_zΨ, cząstki padającej na barierę jest równy prądowi cząstki, która przeszła przez barierę. A zatem prawdopodobieństwo przejścia cząstki naładowanej przez barierę jednorodnego pola elektrycznego jest równe 1.

§5. Podsumowanie

Jest do omówienia kilka wniosków.

Po pierwsze zauważyliśmy, że równanie Diraca w jednorodnym polu elektrycznym nie generuje dodatkowych funkcji falowych przypisanych do ujemnych energii, które mogłyby służyć do opisu antycząstek. Jak to możliwe?

Jeśli zajrzymy, na przykład do [5], to przekonamy się, że szereg prowadzonych tam rozumowań opartych na istnieniu rozwiązań o ujemnej energii jest prowadzonych bez dowodu, że równanie Diraca w danym typie pola A^μ ma w ogóle takowe rozwiązania. To, że równanie swobodne ma takowe, to nie oznacza, że każde inne też ma!

Po drugie, bispinorów będących rozwiązaniami równania Diraca w tym polu nie można normować tak po prostu jak w przypadku swobodnych rozwiązań. Energia i pęd będące ich elementami są teraz funkcjami z i ct, a zatem użycie ich do normowań tak jak we wzorze (32) w [6] jest niedopuszczalne, bo zmienia postać funkcjonalną rozwiązań. Te rozwiązania wolno normować tylko w wybranym punkcie czasoprzestrzeni.

Wróćmy jeszcze do lektury [7]. Autorzy badali tam ruch elektronu w jednorodnym polu elektrycznym, ale za pomocą równania Schrödingera. Jako rozwiązanie otrzymali funkcję Airy’ego wymnożoną przez czynnik normalizacyjny. Jeśli chodzi o zachowanie asymptotyczne, to w dodatku matematycznym §b podano, że w obszarze dużych ujemnych x funkcja ta ma charakter oscylacyjny, natomiast dla dużych dodatnich x funkcja ta ma charakter zaniku wykładniczego.

Jednak gdy zajrzymy do prac [2,3] o charakterze doświadczalnym to dowiemy się, że cząstki przyspieszane w akceleratorze elektrostatycznym w zasadzie zachowują się jak cząstki swobodne. Można je ogniskować, odchylać, po prostu dobrze nimi sterować.

To wskazuje, że jednak rozwiązanie równania Diraca w jednorodnym polu elektrycznym podane przeze mnie prawidłowo opisuje ruch cząstek naładowanych w takim akceleratorze. A więc mechanika kwantowa potrafiła wnieść tu coś nowego, czego nie potrafiła mechanika klasyczna.

LITERATURA

[1] J.Szcząchor, Rozwiązanie równania Diraca w jednorodnym polu elektrycznym - część 2, http://januszszczachor.cba.pl/www/index.php/rownanie-diraca-jednorodne-pole-elektryczne-2.html.

[2] R. J. Van de Graaff, J. G. Trump, W.W. Buchner, Electrostatic generators for the acceleration of charged particles, Reports on Progress in Physics 11, 1(1947).

[3] Praca zbiorowa, Seminarium przeglądowe prac wykonanych przy użyciu „LECHA“, Postępy Techniki Jądrowej, 11, 587-625(1967).

[4] Ch. Kittel, W. D. Knight, M. A. Ruderman, Mechanika, PWN, Warszawa 1975, rozdział 13.

[5] J. D. Bjorken, S. D. Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985, rozdział 5.

[6] J.Szcząchor, Metody rozwiązywania równania Diraca - Część 1, http://januszszczachor.cba.pl/dirac/rownanie_diraca_1.php.

[7] L. D. Landau, E. M. Lifszyc, Mechanika Kwantowa - teoria nierelatywistyczna, PWN, Warszawa 1979, rozdział III, §24. Ruch w polu jednorodnym oraz §b w uzupełnieniu matematycznym.