Rachunek wektorowy w fizyce szkolnej - część 2

Szczegóły

Kategoria: Fizyka szkolna

Opublikowano: poniedziałek, 6 styczeń 2020 15:10

Autor : Janusz Szcząchor

Po przejrzeniu obecnie obowiązujących podręczników z fizyki dla szkół średnich (różnych wydawnictw) dostrzegłem bardzo poważną powierzchowność w programie nauczania co do sposobu wdrażaniu rachunku wektorowego. Jako przykład mogę podać brak dokładnego wyjaśnienia czym różni się pojęcie współrzędnej punktu od współrzędnej wektora, jaka jest różnica między długością wektora, a jego współrzędną. Wątpię, aby uczniowie wynieśli tę wiedzę z lekcji matematyki w szkole podstawowej.

W mojej ocenie przydałoby się jakieś korepetytorium z tej dziedziny dostosowane do poziomu rozwoju absolwenta podstawówki. W przeciwnym wypadku wielu uczniów będzie miało problem ze zrozumieniem tych zagadnień. Wątpię, czy nauczyciele będą mieli czas na lekcji, aby wyjaśniać uczniom takie niuanse. Stąd mój poradnik.

Do jego napisania użyłem tu jako przewodnika po materiale nauczania z fizyki w szkole średniej podręcznika - Marcin Braun, Krzysztof Byczuk, Agnieszka Seweryn-Byczuk, Elżbieta Wójtowicz, Zrozumieć Fizykę 1, Podręcznik dla szkół ponadgimnazjalnych, Zakres rozszerzony, Nowa Era, Warszawa 2016.

§7 Wektor prędkości średniej

Prędkość średnia ciała fizycznego w danym przedziale czasu Δt to iloraz przemieszczenia Δr tego ciała, jakie miało miejsce w ciągu tego przedziału czasu do wartości tego przedziału. Skoro przemieszczenie jest wektorem, to prędkość średnia jest też wektorem.

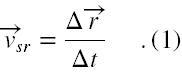
Zakładając, że ruch ciała jest tylko wzdłuż osi X oraz korzystając z tego, że Δr = iΔx możemy wektory w (1) rozpisać na składowe

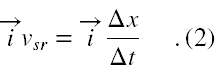
Stąd mamy, że współrzędna wektora prędkości średniej jest równa

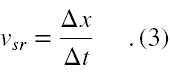
PRZYKŁAD 1: (¹) Turystka porusza się po drodze, którą, zaniedbując jej szerokość, można uznać za linię prostą. Mijając słupek z napisem 250 km turystka skonstatowała, że nie uzupełniła prowiantu w ostatnim zajeździe. Zmuszona była zawrócić i po pół godzinie mijając słupek z napisem 247 km weszła do zajazdu. Z jaką prędkością średnią poruszała się turystka w ciągu ostatniej pół godziny, tj. jaka była wartość współrzędnej tego wektora prędkości, a jaka była długość tego wektora?

Wartości kilometrów na słupkach drogowych należy potraktować jako współrzędne kolejnych położeń turystki na osi X. Zatem od położenia końcowego x₂ = 247 km odejmujemy położenie początkowe x₁ = 250 km i otrzymujemy współrzędną wektora przemieszczenia turystki, czyli Δx = - 3 km.

Korzystając ze wzoru (3) obliczamy wartość współrzędnej wektora prędkości średniej turystki, która jest równa v_sr = - 6 km/h. Mnożąc wersor osi X przez tę ujemną wartość widzimy, że zwrot wektora prędkości średniej jest w kierunku ujemnych wartości osi X. Zatem turystka poruszała się do tyłu osi X.

Co do długości wektora prędkości średniej, to zgodnie ze wzorem (3) w §4 mamy, że długość tego wektora jest równa

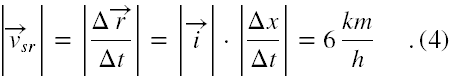
Należy to rozumieć następująco. Na podstawie danej długości wektora prędkości średniej turystki, a nie wartość składowej, możemy tylko powiedzieć, że w ciągu pół godziny turystka przebyła drogę o wartości 3 km, ale nie wiadomo w która stronę, czy do 'przodu', czy do 'tyłu'.

Dowód polega na pomnożeniu wzoru (1) stronami przez Δt, obróceniu stronami oraz stronami wzięciu wartości bezwzględnej. Ponieważ czas płynie tylko do przodu w makroświecie, zatem zawsze Δt > 0. Stąd mamy

Ponieważ ruch jest prostoliniowy, a turystka w ciągu czasu Δt = 1/2 h nie zawraca, więc |Δr| jest drogą turystki w tym ruchu.

§8 Wektor prędkości chwilowej

Prędkość chwilowa ciała fizycznego to graniczna prędkość średnia tego ciała uzyskana w wyniku zmierzania z przedziałem czasu Δt, w ciągu którego obliczamy tę prędkość średnią, do 0.

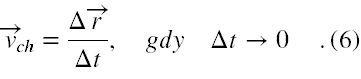
Gdybyśmy chcieli "ręcznie" obliczyć prędkość chwilową, to polegałoby to na kolejnym obliczaniu prędkości średniej w coraz krótszych przedziałach czasu Δt, ale w ten sposób, że to malenie przedziału czasu musiałoby być bardzo powolne i patrzeniu, czy w wyniku tego otrzymujemy dla konkretnej chwili czasu t jakiś stały wektor.

W praktyce do tego służą przyrządy takie jak prędkościomierz, albo narzędzia analizy matematycznej, jeżeli jest możliwe ustalenie zależności funkcyjnej od czasu wektora położenia ciała.

Wykorzystując wzór (2) widzimy, że w przypadku ruchu wzdłuż osi X współrzędna prędkości chwilowej jest po prostu równa

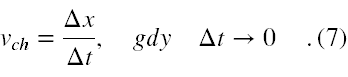
§9 Równania ruchu w fizyce szkolnej

Podczas omawiania typowych rodzajów ruchu często pojawia się zagadnienie wyznaczenia równania ruchu. Zwykle chodzi tu o podanie zależności współrzędnych wektora położenia ciała fizycznego od czasu w formie algebraicznej jako funkcji czasu lub w formie wykresu graficznego. Jednak obie te metody mogą nie być jednakowo dostępne na poziomie szkoły średniej. Przyjrzyjmy się poniższemu wykresowi.

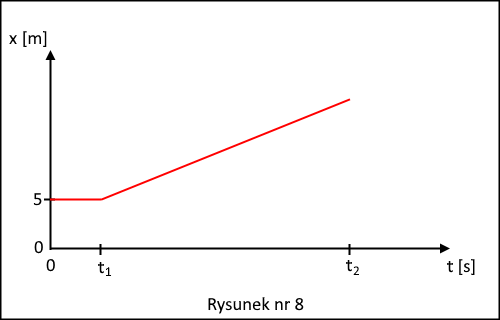
Na wykresie widać, że ciało przez pewien czas przyjmuje stałe położenie x = 5 m, czyli spoczywa, a następnie porusza się ze stałą prędkością chwilową (jak się niedługo przekonasz). Jednak zapisanie tego wykresu jednym wzorem algebraicznym nie jest sprawą trywialną jako, że są to połączone ze sobą dwie funkcje liniowe o różnym współczynniku nachylenia (²).

Na poziomie szkoły średniej nie ma innego sposobu, jak dzielić tego typu wykres na odpowiednie części i rozważać formę równania ruchu stosownymi przedziałami czasu.

§10 Ruch jednostajny prostoliniowy

Ruch jednostajny prostoliniowy, to chyba najprostszy przykład ruchu, jeśli pominąć spoczynek. W nim torem ruchu jest linia prosta, a prędkość chwilowa ciała jest stała. Ponieważ prędkość to wektor, więc oznacza to stałość wartości, kierunku i zwrotu. Zatem ciało w tym ruchu nie zawraca. Zapisujemy to następująco

Zbadajmy zatem jakie konsekwencje za sobą niesie definicja tego szczególnego rodzaju ruchu. Podstawowym zagadnieniem jest tutaj podanie równania ruchu, czyli znalezienie zależności algebraicznej wektora położenia od czasu dla ciała w tym ruchu.

Skoro jest to ruch prostoliniowy, więc możemy przyjąć, że ruch odbywa się tylko wzdłuż osi X, a poszukiwana przez Nas zależność w ogólności powinna mieć taką postać

r(t) = ix(t). (9)

Jak zatem z zależności (8) otrzymać ile jest równe x(t) dla tego ruchu (³)? Wykorzystamy tu fakt, że jeśli prędkość chwilowa jest stałym wektorem w jakimś ruchu, to wtedy prędkość średnia jest równa prędkości chwilowej. Spróbujemy podać dowód intuicyjny (⁴).

Zróbmy wykres graficzny zależności współrzędnej prędkości chwilowej od czasu w tym ruchu. Skoro wartość wektora prędkości chwilowej jest stała w czasie, więc współrzędna jest albo stale dodatnia, albo stale ujemna (⁵). Wybierzmy przykładową wartość dodatnią, a jej zależność od czasu w wybranym przedziale od czasu powinna mieć postać, rysunek nr 9.

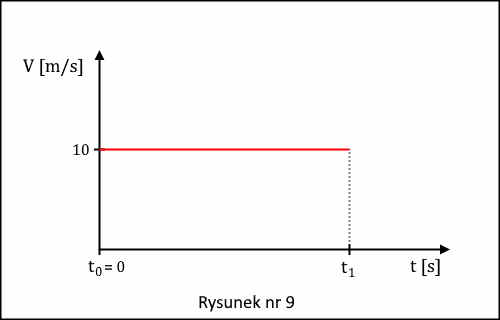
Patrząc na ten wykres widzimy, że skoro mamy ciągle tę samą wartość współrzędnej w pewnym przedziale czasu od t₀ do t₁, to "średnia" tej wartości zarówno w tym przedziale czasu, jak i w dowolnym jego podprzedziale jest równa tej wartości. Zatem rzeczywiście w ruchu tym wartość wektora prędkości średniej jest równa wartości wektora prędkości chwilowej.

Oznaczmy wartość prędkości chwilowej jako v (jest to wielkość zawsze dodatnia). Natomiast wartość prędkości średniej jest dana wzorem (4). Przyrównajmy je do siebie.

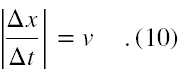
Wprowadźmy następujące oznaczenia. Niech współrzędna położenia ciała w chwili t₀ jest oznaczona jako x₀, a w chwili t₁ jako x₁. Zatem wzór (10) zamienia się w

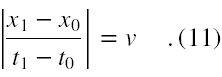
Wybierzmy jak na rysunku nr 9, że t₀ = 0, a t₁ oznaczmy po prostu wtedy jako t, a odpowiadającą tej chwili współrzędną położenia jako po prostu x. Otrzymujemy wtedy wzór

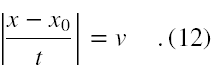
Skoro mamy wartość bezwzględną, to musimy rozpatrzyć dwa przypadki. Niech najpierw wielkość pod znakiem wartości bezwzględnej jest dodatnia, wtedy otrzymujemy po prostych przekształceniach (opuszczamy znak wartości bezwzględnej, mnożymy stronami przez t, przenosimy x₀ na drugą stronę ze zmienionym znakiem)

Mamy tutaj ruch do przodu osi X (nawet jeśli x₀ < 0, to po dostatecznie długim okresie czasu t współrzędna x stanie się dodatnia).

W drugim przypadku, gdy wartość bezwzględna jest ujemna mamy (opuszczamy znak wartości bezwzględnej, wstawiamy minus przed ułamkien na lewej stronie, mnożymy stronami przez t, przenosimy x₀ na drugą stronę ze zmienionym znakiem)

Mamy tutaj ruch do tyłu osi X (nawet jeśli x₀ > 0, to po dostatecznie długim okresie czasu t współrzędna x stanie się ujemna).

Obydwa te przypadki można połączyć. Zauważmy, że gdy mamy wektor prędkości skierowany do przodu osi X, to jego składowa jest dodatnia, a gdy jest do tyłu, to jest ujemna. Zatem możemy zinterpretować, że wielkość, która występuje przy t wzięta wraz ze znakiem (w obu powyższych przypadkach), to jest to współrzędna wektora prędkości chwilowej względem osi X.

Zatem równanie ruchu naszego ciała poruszającego się ruchem jednostajnym prostoliniowym, to

gdzie teraz x, x₀ oraz v, to współrzędne odpowiednich wektorów (we wzorach (13) oraz (14) v, przypominam, to długość wektora prędkości ciała).

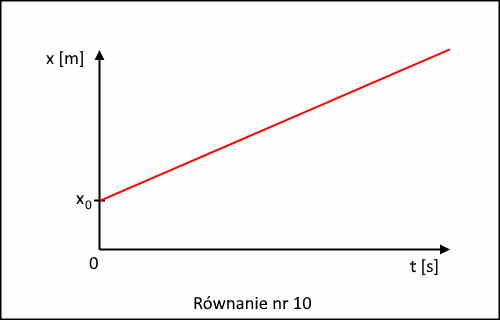
Przejdźmy do analizy graficznej tej zależności. Równanie (15), to matematyczne równanie funkcji liniowej, przy czym x₀ pełni rolę wyrazu wolnego, a v - współczynnika kierunkowego prostej mówiącego jak prosta ma być nachylona do osi X, t pełni rolę zmiennej niezależnej, a x zmiennej zależnej. Jeżeli v > 0 i x₀ > 0, to jej wykres ma zatem postać, rysunek nr 10.

A jeśli v < 0 i x₀ > 0, to otrzymujemy następujący wykres, rysunek nr 11.

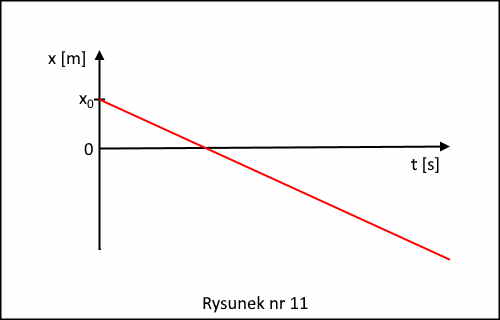
Pozostaje nam jeszcze policzenie w tym ruchu drogi jaką ciało pokonało między chwilą t = 0, a dowolną inną chwilą t. Ponieważ tutaj droga, to długość wektora przemieszczenia, zatem zgodnie ze wzorem (3) z §4 oraz wzorem (11) z §6 mamy

s = |Δr(t)| = |i|·|Δx(t)| = |x(t) - x₀| = |vt| = |v|t. (16)

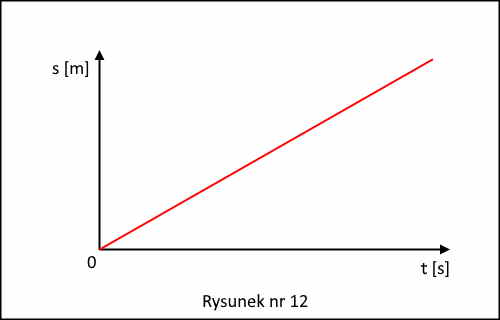
Widzimy stąd, że droga s przebyta przez ciało w ruchu jednostajnym prostoliniowym jest wprost proporcjonalna do czasu t, rysunek nr 12.

(¹) Przykład zainspirowany treścią przykładu ze strony 29 podręcznika [1].

(²) Można to zrobić na przykład wykorzystując funkcję skokową Heaviside'a.

(³) Gdybyś znał rachunek całkowy zajęłoby to Nam kilka sekund.

(⁴) Ścisły dowód tego faktu ponownie wymaga użycia rachunku całkowego.

(⁵) Albo stale równa 0, ale wtedy mamy spoczynek.

BIBLIOGRAFIA

[1] M. Braun, K. Byczuk, A. Seweryn-Byczuk, E. Wójtowicz, Zrozumieć Fizykę 1, Podręcznik dla szkół ponadgimnazjalnych, Zakres rozszerzony, Nowa Era, Warszawa 2016.