W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 28

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano:poniedziałek, 17 grudzień 2018 19:05

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

Zadanie nr 2.103 , B.Mendel, J.Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Z jaką prędkością kątową powinno obracać się wokół osi symetrii naczynie stożkowe (rys. 2.38), aby kulka umieszczona w naczyniu i obracająca się razem z naczyniem wyleciała na zewnątrz? W chwili początkowej odległość kulki od osi obrotu wynosi R = 6 cm, kąt 2α = 60°.

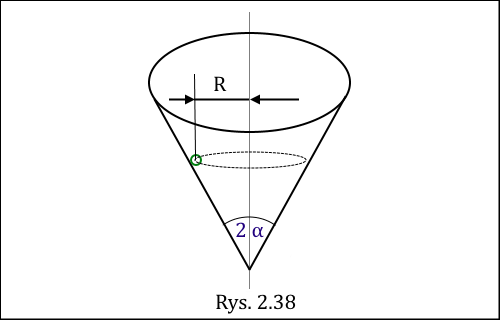
Rozwiązanie

Zacznijmy od wstępnej uwagi, że pewna część tekstu tego zadania jest sformułowana być może trochę niejasno. Chodzi po pierwsze o sens wyrażenia "kulka umieszczona w naczyniu i obracająca się razem z naczyniem wyleciała na zewnątrz". Może ono u ucznia wywołać konsternację.

Jest to pewien skrót myślowy, który ma dostarczyć uczniowi informacji, że kulka porusza się po okręgu z taką samą prędkością kątową (mającą stałą wartość) co i naczynie stożkowe, oznaczmy ją literą ω, nie jest do niego przymocowana, a jednocześnie zapewnić, że nie będzie on dociekał jak to się faktycznie dzieje, że kulka się w ogóle obraca, co jest źródłem jej ruchu. Dociekliwy młody umysł może nie chcieć się temu podporządkować.

Ponadto tekst zadania nie zawiera oznaczeń wszystkich istotnych w tym zadaniu wielkości fizycznych. Stąd symbole te trzeba samemu uzupełnić.

Zadanie rozwiążemy w układzie odniesienia związanym z podłożem, na którym stoi obracające się naczynie.

Na kulkę z całą pewnością działa siła grawitacji objawiająca się jako jej ciężar. Zatem oznaczmy jej masę jako m, a ciężar jako P (¹). Nie powinno ulegać wątpliwości, że kulka porusza się ruchem jednostajnym po okręgu o promieniu R, tym samym musi na nią działać siła dośrodkowa zmuszająca ją do tego ruchu. Siła ta oczywiście pochodzi od obracającego się naczynia, którego krzywizna nie pozwala poruszać się kulce po linii prostej.

Siłę tę oznaczmy jako N, zwyczajowo nosi ona nazwę siły nacisku. Jest skierowana wzdłuż prostej prostopadłej do powierzchni naciskającej. Układ dotychczas zidentyfikowanych sił przedstawia rysunek nr 1.

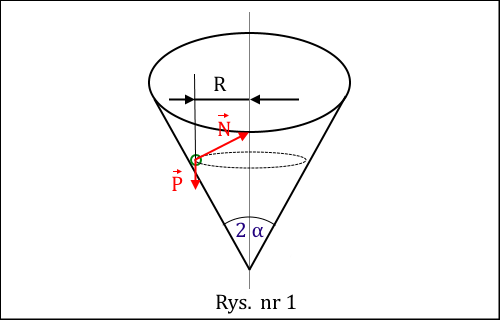
Załóżmy, że wartość prędkości kątowej jest taka, że kulka jeszcze nie porusza się w górę (jeżeli kulka ma wylecieć na zewnątrz, to będzie musiała posiadać większą od zera składową prędkości skierowaną do góry, w kierunku pionowym).

Oznacza to, że wypadkowa F_w siły nacisku N oraz ciężaru P jest skierowana poziomo i to ona jest siłą dośrodkową zmuszającą kulkę do ruchu po okręgu - rysunek nr 2.

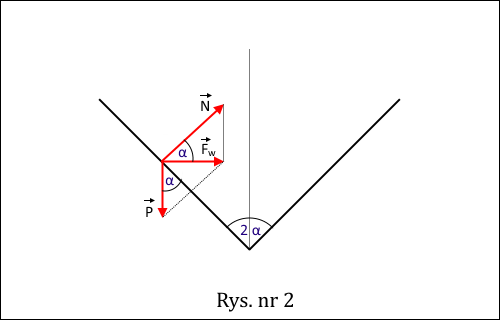
Wzrost prędkości kątowej ω kulki (zgodnie z treścią zadania, z powodu szybszego obracania się stożkowego naczynia) oznacza wzrost siły nacisku N (²). Jednocześnie nie ulega wątpliwości, że ciężar kulki P się nie zmienia. Stąd teraz siła wypadkowa F_w będzie skierowana trochę w górę ponad kierunek poziomy i kulka zacznie poruszać się w górę. To w zasadzie wystarczy do rozwiązania zadania (³).

Jednak takie wyjaśnienie osobie początkującej w fizyce może okazać się niejasne i nasuwać szereg wątpliwości. Dla mnie, gdy byłem uczniem, tak skromne wyjaśnienia oczywiście były nie do zaakceptowania. Dlatego zadanie będziemy analizować dalej.

Siła nacisku N jest siłą kontaktową, działa tylko gdy kulka styka się z naczyniem. Jakakolwiek próba "odlotu" kulki skończy się jej spadkiem na naczynie spowodowanym przez jej ciężar. Zatem, "wylatując" z naczynia kulka faktycznie porusza się po powierzchni naczynia. Oznacza to, że musi wtedy działać na kulkę skierowana w górę, niezerowa siła styczna do powierzchni naczynia.

Rozłóżmy ciężar kulki P na składowe, P_n będącą siłą dociskającą kulkę do naczynia oraz P_s ściągającą ją w dół, po powierzchni naczynia - rysunek nr 3.

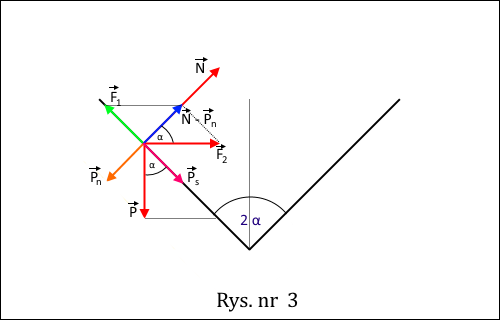
Siła P_n zmniejsza siłę N do wypadkowej N - P_n. Ta wypadkowa rozkłada się na składową F₂ zmuszającą kulkę do ruchu po okręgu (F₂ jest oczywiście równa F_w z rysunku nr 2) oraz F₁ wywołująca ruch kulki w górę.

Jeżeli siły F₁ i P_s będą się równoważyły, to kulka nie będzie się poruszać w kierunku pionowym. Gdy zmniejszymy ω, a tym samym F₁, to kulka będzie się poruszać w dół. W przeciwnym przypadku w górę. Warunek równowagi sił F₁ i P_s zapisany przy pomocy ich wartości, to oczywiście

F₁ = P_s . (1)

Aby wyznaczyć F₁ wcale nie potrzebujemy znać N. Możemy ją wyznaczyć z rysunku nr 3

sin α = F₁ / F₂ . (2)

Podobnie jest z P_s

cos α = P_s / P . (3)

Skoro F₂ jest siłą dośrodkową, zatem jej wartość jest dana jako mω²R. Stąd (1) możemy zapisać jako

mω²Rsinα = mgcosα . (4)

To daje oczywisty już wynik

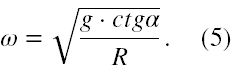
Uwagi

Oczywiście zadanie można rozwiązać w nieinercjalnym układzie odniesienia związanym z poruszającą się kulką. Jednak rozwiązanie w układzie inercjalnym, jest moim zdaniem, bardziej pouczające, bo analizujemy działanie rzeczywistych sił.

(¹) Pogrubienie litery w tym artykule oznacza wektor.

(²) Dla ucznia może to nie być takie oczywiste. Wzrost prędkości kątowej ω oznacza wzrost prędkości liniowej, stycznej do toru. To oznacza wzrost wartości wektora pędu kulki, który też jest styczny do toru. Im większy taki pęd, tym potrzebna jest większa siła, aby zmusić kulkę do ruchu po okręgu zamiast po linii prostej. Naczynie stożkowe, jako że jest sztywne, jest w stanie dostarczyć dowolną siłę (oczywiście w granicach swojej sztywności). Dlatego mamy wzrost siły nacisku.

(³) Rozwiązanie zadania nr 121, S. U. Gonczarenko, Zadania z fizyki, Wydawnictwo Naukowo - Techniczne, Warszawa 1974. W tym zadaniu kąt oznaczony jako α, to inny kąt niż w zadaniu ze zbioru Mendla. Jest on równy 90 - α, gdzie α to kąt z zadania ze zbioru Mendla.