W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - poziom podstawowy, część 6

Szczegóły

Kategoria: Zadania z Fizyki - poziom podstawowy

Opublikowano: niedziela, 11, wrzesień 2016 07:07

Autor : Janusz Szcząchor

zadanie nr VII.15, Bogdan Mendel, Janusz Mendel - Zbiór zadań z fizyki - kurs podstawowy, WSiP, Warszawa 1976

Ciało o ciężarze równym 600 N zawieszone jest na dźwigarze, którego wymiary wynoszą: a = 30 cm, b = 40 cm, c = 50 cm. Wyznacz siły P₁ i P₂ działające jak na rysunku 29 przyjmując, że 1 cm odpowiada sile 100 N.

Rozwiązanie

Zadanie można by łatwo rozwiązać używając funkcji trygonometrycznych lub chociażby twierdzenia Pitagorasa. Jednak zadanie jest przeznaczone dla uczniów, którzy jeszcze nie znają tych narzędzi i dlatego rozwiążemy je bez nich.

Na początek na rysunku nr 1 przedstawimy sytuację zadaniową jeszcze bez rozkładu ciężaru ciała na składowe i zastanowimy się na jakie składowe ten ciężar powinien się rozkładać.

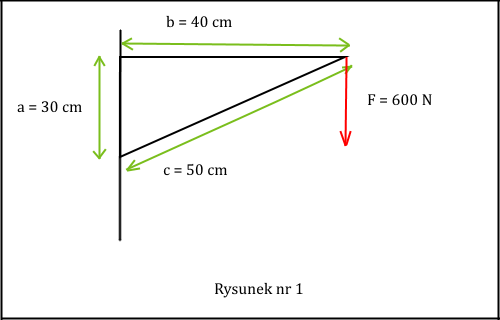
Ten dźwigar to nic innego jak trójkąt prostokątny wykonany z wytrzymałego materiału, na przykład stali. Rozkład ciężaru może następować wyłącznie wzdłuż ramion dźwigaru, bo to on utrzymuje ciężar. Ciężar działając w dół oczywiście ściska bok o długości 50 cm, a zatem jedna składowa musi działać wzdłuż tego boku. Na rysunku w zbiorze zadań jest ona nazwana jako P₂.

Druga składowa powinna działać rozciągająco na ramię o długości 40 cm działając w prawo. Ta siła została oznaczona w zbiorze jako P₁.

W tym przypadku rozkład ciężaru 600 N dokonany metodą równoległoboku oznacza nic innego, że siły P₁ i P₂ muszą tworzyć ramiona pewnego równoległoboku, a ciężar musi być jego przekątną - spójrzmy na rysunek nr 2.

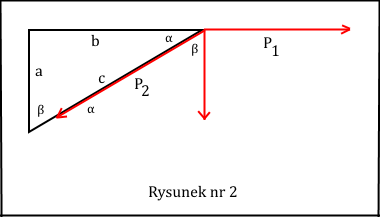
Przyglądając się równoległobokowi (czerwone wektory) widzimy, że składa się on z dwóch trójkątów prostokątnych. Każdy z tych trójkątów ma odpowiednie kąty równe odpowiednim kątom trójkąta - dźwigara. W takiej sytuacji wszystkie te trójkąty są do siebie podobne. Zatem na mocy twierdzenia (¹) o wielobokach podobnych oznacza to, że odpowiednie boki wszystkich tych trójkątów są do siebie proporcjonalne. Stąd możemy napisać, że

a/600 N = b/P₁ = c/P₂,

czyli

30 cm/600 N = 40 cm/P₁ = 50 cm/P₂ .

Stąd możemy już dać odpowiedź.

Odpowiedź: Siła P₂ jest równa 1000 N, a P₁ jest równa 800 N.

LITERATURA

¹ W. Leksiński, B. Macukow, W. Żakowski, Matematyka w zadaniach , Wydawnictwo Naukowo-Techniczne, Warszawa 1981, § 6.2. Twierdzenie Talesa. Jednokładność. Figury podobne