W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - poziom podstawowy, część 4
- Szczegóły
- Kategoria: Zadania z Fizyki - poziom podstawowy
- Opublikowano: niedziela, 04, wrzesień 2016 11:54
- Autor : Janusz Szcząchor
zadanie nr VI.60, Bogdan Mendel, Janusz Mendel - Zbiór zadań z fizyki - kurs podstawowy, WSiP, Warszawa 1976
Ile wody należy dolać do 875 cm3 benzyny, aby średnia gęstość tak powstałej cieczy była równa gęstości eteru? Gęstość wody ρwody = 1000 kg/m3, gęstość benzyny ρbenzyny = 680 kg/m3, a gęstość eteru ρeteru = 720 kg/m3.
Rozwiązanie
Pierwszy podstawowy problem w tym zadaniu polega na pytaniu, czy Ty czytelniku wiesz co to jest średnia gęstość cieczy. Na wszelki wypadek zaczniemy od wyjaśnienia tego zagadnienia.
Jak wspomniano wyżej w treści zadania, gęstość benzyny jest mniejsza od gęstości wody, a ponieważ obie ciecze się ze sobą nie mieszają, więc woda znajdzie się na dnie naczynia, a benzyna wyżej na niej, mniej więcej tak jak na poniższym rysunku.
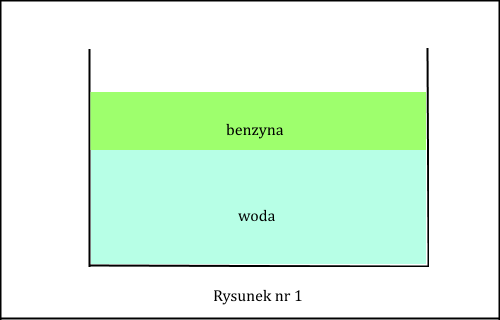
W oparciu o powyższy rysunek spróbuję teraz wyjaśnić co to jest średnia gęstość cieczy. Przyjmijmy dla celów zadania, że objętość wody w naczyniu to V1, a benzyny to V2. Średnią gęstość cieczy w naczyniu liczymy z ogólnego wzoru na gęstość, czyli
ρ = m/V, (1)
gdzie m oznacza sumę mas obu cieczy, a V to suma objętości obu cieczy. Z uwagi na dane w zadaniu, masa każdej cieczy jest dana znowu ze wzoru związanego z jej gęstością, czyli
mwody = ρwody · V1, (2)
mbenzyny = ρbenzyny · V2 . (3)
Zatem średnia gęstość to
ρśrednia = (mwody + mbenzyny)/(V1 + V2), (4)
czyli
ρśrednia = (ρwody · V1 + ρbenzyny · V2 )/(V1 + V2). (5)
Możemy teraz przystąpić do analizy wzoru (5) z punktu widzenia danych tego zadania. Jest chyba oczywistym, że za gęstość średnią należy rozumieć gęstość eteru, 875 cm3 to V2 . Zatem niewiadomą jest wielkość V1 . Aby móc ją obliczyć musimy przekształcić wzór (5) tak, aby otrzymać wzór na V1 . Zgodnie z regułami algebry robimy to w następujących krokach.
Zatem we wzorze (5) zamieniamy słowo 'średnia' na 'eteru' oraz mnożymy ten wzór stronami przez ( V1 + V2) i otrzymujemy
ρeteru · (V1 + V2) = ρwody · V1 + ρbenzyny · V2 . (6)
Teraz rozpisujemy lewą stronę (6) na sumę, wyraz z V2 przenosimy ze zmienionym znakiem na prawą stronę, a wyraz z V1 po prawej stronie również przenosimy z przeciwnym znakiem, ale na lewą stronę równania i otrzymujemy
ρeteru · V1 - ρwody · V1 = ρbenzyny · V2 - ρeteru · V2 . (7)
Po obu stronach równania możemy wyłączyć objętości przed nawias, po lewej V1 , a po prawej V2 i mamy
(ρeteru - ρwody) · V1 = (ρbenzyny - ρeteru) · V2 . (8)
I w końcu mnożymy stronami (8) przez -1, aby odwrócić kolejność wyrazów w nawiasach, aby uniknąć w nich ujemnych wartości, a następnie dzielimy stronami (8) przez ( ρwody - ρeteru) i otrzymujemy ostatecznie
V1 = [ V2·(ρeteru - ρbenzyny)]/(ρwody - ρeteru) . (9)
Osobna kwestia, to obliczenia numeryczne. W tym celu musimy uzgodnić jednostki. Najmniej pracochłonne będzie zamienienie 875 cm3 na m3 ( w przeciwnym wypadku musielibyśmy zamienić wszystkie gęstości). A zatem
1 m3 = 100 cm · 100 cm · 100 cm = 1 000 000 cm3 . (10)
Stąd 875 musimy podzielić przez 1 000 000, czyli przesuwamy przecinek o 6 pozycji w lewo i mamy, że
V2 = 0,000875 m3 . (11)
W końcu objętość wody, którą musimy dolać to
V1 = 0,000875 m3 · (720 kg/m3 - 680 kg/m3)/(1000 kg/m3 - 720 kg/m3)
= 0,000875 m3 · (40)/(280) = 0,000125 m3 . (12)
Odpowiedź: Należy dolać 125 cm3 wody.
