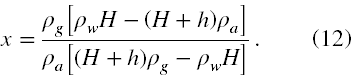W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 25

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: piątek, 11, listopad 2016 14:26

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 6.4, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

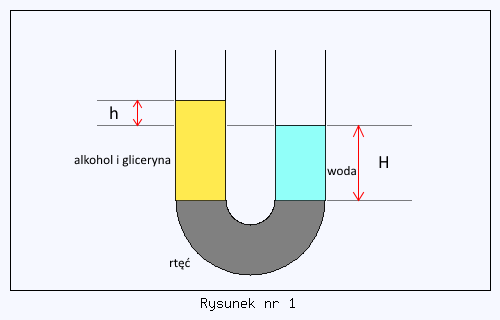
W rurce w kształcie litery U znajdują się dwie ciecze przedzielone słupkiem rtęci (rys. 6.3); w lewej rurce - mieszanina alkoholu z gliceryną, a w prawej woda. Poziom cieczy w lewym naczyniu jest wyższy o h = 1 cm od poziomu cieczy w prawym. Wysokość słupa wody wynosi H = 8 cm. W jakim stosunku wagowym wymieszana jest gliceryna z alkoholem? Tablice gęstości - na końcu książki.

Rozwiązanie

Jako wstęp do rozwiązania tego zadania proponuję zapoznać się z artykułem W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Gimnazjum część 4, ponieważ przedstawionych tam wyjaśnień nie będę tu powtarzał.

Na samym początku warto zauważyć, że rtęć nie ma wpływu na sytuację zadania, ona tylko przenosi ciśnienie. Skoro oba słupy cieczy, lewy i prawy, są nieruchome to oznacza, że ciśnienia w obu ramionach się już wyrównały. Zatem możemy być pewni, że ciśnienie słupa alkoholu z gliceryną jest równe ciśnieniu wody, patrz rysunek nr 1.

Wprowadzając czytelne sygnatury " L " dla gęstości cieczy w lewym ramieniu oraz " w " dla wody w prawym ramieniu możemy zapisać powyższą równość w formie następującego równania

Przyspieszenie ziemskie skrócimy stronami przy najbliższej okazji. Zajmijmy się teraz problemem mieszaniny. Pytanie jest o stosunek wagowy wymieszania gliceryny z alkoholem. Oczywiście nazwijmy go " x " i jest on równy

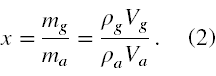
Przy pomocy nieznanych zmiennych, V_g i V_a użytych w (2) możemy wyrazić gęstość mieszaniny zawartej w lewym ramieniu jako

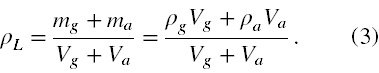
Przystępujemy do przekształceń i oznaczamy jako α iloraz

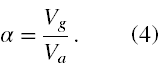
Wtedy wzór (2) możemy zapisać jako

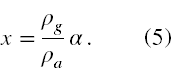
We wzorze (3) dzielimy licznik i mianownik przez V_a i otrzymujemy

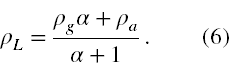
Ze wzoru (1) obliczamy, że ρ_L jest równe

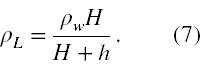
Przyrównujemy do siebie wzory (6) oraz (7)

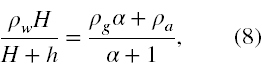
a następnie wyliczamy ile jest α prowadząc kolejne przekształcenia

grupując wyrazy z α z odpowiednimi znakami po jednej stronie równości, a pozostałe podobnie po drugiej

W końcu α jest równe

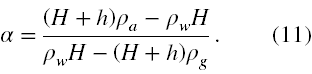
Ostatecznie wstawiamy wzór (11) do wzoru (5), mnożymy dla elegancji licznik i mianownik przez -1 i otrzymujemy ostateczny wynik