Rachunek różniczkowy i całkowy w fizyce szkolnej - część 10

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: czwartek, 18, maj 2017 11:42

Autor : Janusz Szcząchor

zadanie nr 2.29, Henryk Kaczorek, Zbigniew Słówko - "Zbiór zadań z fizyki", WSiP, Warszawa 1981

Przekrój tłoka maszyny parowej (dwustronnej) wynosi S = 100 cm², suw h = 50 cm. Para dostaje się do cylindrów pod ciśnieniem p = 200 kPa, które na każdy l = 1 cm drogi tłoka zmniejsza się o Δp = 2 kPa. Jaka jest moc maszyny, jeżeli wał się obraca z częstością f = 240 obr/min?

Rozwiązanie

Zanim przystąpimy do właściwych rachunków przeanalizujmy działanie maszyny parowej schematycznie pokazanej na rysunku nr 19 w tymże zbiorze zadań, bowiem bez tego nie jest możliwe prawidłowe zrozumienie zadania.

Widzimy, że pełen okres ruchu tłoka składa się z pełnego przesunięcia się przez niego z lewa na prawo przez całą długość cylindra, a następnie to samo z prawa na lewo. W tym samym czasie wał wykonuje jeden obrót. A zatem w ciągu jednej minuty wał wykona 240 obrotów, a tłok pokona drogę równą 2h 240 krotnie .

Stwierdzenie, że jest to maszyna parowa dwustronna oznacza, że zarówno podczas ruchu tłoka w lewo, jak i w prawo wpływa do cylindra sprężona para, a zatem w obu przypadkach maszyna parowa wykonuje pracę użyteczną. Oznacza to podwojenie mocy maszyny.

Na koniec pozostaje zauważenie, że stwierdzenie w treści zadania, iż na każdy 1 cm drogi tłoka ciśnienie robocze pary zmniejsza się o 2 kPa po pierwsze oznacza, że ciśnienie od którego zależy praca wykonana przez maszynę parową jest funkcją drogi tłoka maszyny. Stąd w rozwiązaniu nie możemy posłużyć się wzorem

ΔW = pΔV, (1)

bo p nie jest stałe, a musimy użyć jego całkowego odpowiednika

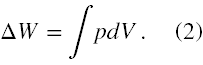
W przypadku wzoru (1) ΔV = Sh, czyli przyrost objętości pary podczas ruchu tłoka jest równy po prostu objętości cylindra (tak właściwie, to zamiast zmiennej h powinno się pisać Δh, ale pozostańmy przy oznaczeniach autorów).

We wzorze (2) dV = Sdx, gdzie dV to różniczkowy przyrost objętości pary, a dx to różniczkowy przyrost drogi tłoka, w granicach którego możemy założyć, że ciśnienie p jest stałe. Widzimy też, że różniczka dV nie jest niezależna. Rzeczywistą zmienną niezależną jest zmienna x, czyli droga tłoka. Przyjmuje ona wartość 0 w jego skrajnym lewym położeniu i h w skrajnym prawym. Skoro przekrój tłoka S jest stałą, zatem w oparciu o wzór (2) możemy powiedzieć, że praca maszyny parowej wykonana podczas pełnego ruchu tłoka z lewa na prawo to

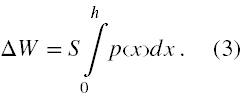
Aby ustalić jaka jest zależność funkcyjna ciśnienia p od x zauważmy, że gdy x = 0, to ciśnienie jest równe p. Stwierdzenie, że na każdy centymetr drogi tłoka ciśnienie zmniejsza się o 2 kPa, to nic innego jak podanie szybkości z jaką maleje ciśnienie wraz z drogą tłoka. Dzięki temu możemy napisać proporcję

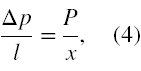
gdzie za pomocą P oznaczyliśmy spadek ciśnienia w cylindrze dla dowolnego x. Zatem zależność ciśnienia p(x) w cylindrze od położenia tłoka x , to

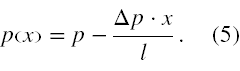
Zatem musimy wykonać całkę

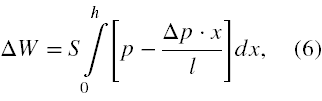
która jest równa

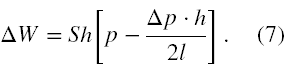
Jak powiedzieliśmy wyżej jest to maszyna dwustronna, a zatem w ciągu jednego obrotu wału maszyna wykonuje pracę 2·ΔW, a skoro w ciągu jednej minuty wykona 240 obrotów zatem jej moc w kJ na minutę, to

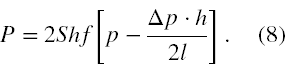
Taki jest wynik zgodnie z danymi zadania. Aby podać moc w kW należy zauważyć, że f to 4 obr/s.