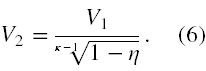W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 26

Szczegóły
Kategoria: Zadania z fizyki
Opublikowano: czwartek, 18, maj 2017 11:42
Autor : Janusz Szcząchor


O mnie:
Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 2.21, Henryk Kaczorek, Zbigniew Słówko - "Zbiór zadań z fizyki", WSiP, Warszawa 1981

W idealnej maszynie chłodniczej wykorzystującej odwrotny cykl Carnota, następuje przekazywanie ciepła od ciała o temperaturze T2 = 253 K (-20°C) do wody o temperaturze T1 = 283 K (10°C). Znajdź ciepło Q2 pobrane od chłodzonego ciała w czasie, gdy praca sił zewnętrznych nad chłodziarką wynosiła W = 118,6 kJ.

zadanie nr 2.19, Henryk Kaczorek, Zbigniew Słówko - "Zbiór zadań z fizyki", WSiP, Warszawa 1981

Oblicz objętość końcową V2 podczas adiabatycznego rozprężania V1 = 3 dm3 gazu w silniku Carnota, którego sprawność wynosi η = 25 %. Stosunek Cp/CV = κ = 2.

Rozwiązanie zadania 2.21

Rozwiązanie tego zadania stanie się proste, jeżeli zauważymy, że sprawność silnika cieplnego w cyklu Carnota, w którym substancją roboczą jest gaz doskonały jest dana nie tylko poprzez ogólny wzór wyrażający ją poprzez ciepło, ale także poprzez temperatury i nie ma tu znaczenia czy silnik Carnota pracuje jako silnik cieplny, czy też jako maszyna chłodząca.

Zatem sprawność maszyny chłodzącej możemy wyrazić jako

sprawność wyrażona przez ciepła

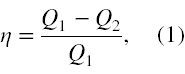
gdzie Q2 to ciepło usuwane ze zbiornika o niższej temperaturze T2, a Q1 to ciepło dostarczane do zbiornika o wyższej temperaturze T1. Biorąc pod uwagę, że praca sił zewnętrznych nad chłodziarką jest dana jako W = Q1 - Q2 możemy wzór (1) wyrażając przez dane zadania zapisać jako

sprawność wyrażona przez dane zadania

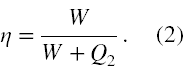
Z drugiej strony wyrażając sprawność poprzez temperatury zbiorników z ciepłem możemy otrzymać następującą równość

porównanie sprawności wyrażonej przez dane zadania z tą daną przez temperatury

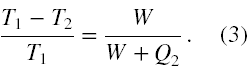
Wykorzystując własność proporcji, na podstawie wzoru (3) możemy zapisać, że ( T1 - T2 )( W + Q2 ) = T1· W. Po wykonaniu odpowiednich przekształceń algebraicznych otrzymujemy z tej równości rozwiązanie w postaci wzoru (4)

rozwiązanie, wzór na ciepło drugie

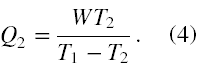
Rozwiązanie zadania 2.19

Gaz roboczy w silniku Carnota podczas rozprężania adiabatycznego przechodzi od stanu opisanego parametrami p1, V1, T1 do stanu opisanego parametrami p2, V2, T2 nie przestając być gazem doskonałym. A zatem ma do niego zastosowanie poniższa konsekwencja równania Clapeyrona

wniosek z równania Clapeyrona

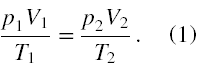
Zauważmy, że parametry ciśnienie, objętość i temperatura tworzą w tym równaniu trzy pary, a raczej trzy ilorazy. Iloraz temperatur da się określić poprzez podaną w zadaniu sprawność, czyli

iloraz temperatur wyrazony poprzez sprawność

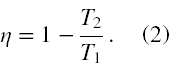
Z kolei iloraz ciśnień da się określić na podstawie konsekwencji wynikającej ze związku ciśnienia i objętości w przemianie adiabatycznej pVκ = const., czyli

iloraz ciśnień wynikający z prawa przemiany adiabatycznej

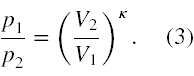
Zatem podstawiając wnioski ze wzorów (2) i (3) do (1) otrzymujemy związek między V1 i V2 w następującej postaci

zależność ilorazu objętości od sprawności

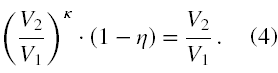
Wzór (4) dzielimy stronami przez V2 i (1 - η), mnożymy stronami przez (V1)κ. Otrzymujemy

wyrażenie na kappa minus jeden potęgę objętości

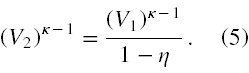
Pozostaje wykonać stronami pierwiastkowanie rzędu κ-1 i ostateczny wynik to

wyrażenie na objętość