Co to jest funkcja falowa i po co jej używamy?

Szczegóły

Kategoria: Fizyka szkolna

Opublikowano: piątek, 23, październik 2015 15:33

Autor : Janusz Szcząchor

1. Na czym polega trudność przy wyjaśnianiu czym jest funkcja falowa?

Podstawową zasadą w nauczaniu jest zasada przystępności nauczanego materiału dla osób nauczanych. Oznacza ona między innymi, że metody nauczania muszą być dostosowane do poziomu intelektualnego uczących się. W przypadku fizyki jest to szczególnie trudne, bo jest ona nauką abstrakcyjną. Dlatego na wstępnym poziomie jej nauczania należy starać się wykorzystywać jak najbardziej metody praktyczne, a abstrakcję fizyczną wprowadzać powoli, stopniowo wchodząc na coraz wyższe jej poziomy.

Stąd w szkole najlepiej posługiwać się doświadczeniem. Następnie mając wyniki liczbowe uzyskane metodą doświadczalną można starać się ustalić wzory matematyczne, które będą je reprodukować. Mając uzyskane wzory można próbować przekonać uczącego się, że wynikają one z jakiejś bardziej ogólnej zasady - fizycznego prawa.

Jeśli chodzi o mechanikę kwantową, to każdy uczeń szkoły średniej jest na tym wstępnym etapie jej nauczania. Dlatego jak najbardziej pożądanym byłoby zbadanie własności funkcji falowej w doświadczeniu.

Niestety, nie jest możliwy pomiar amplitudy funkcji falowej w sposób bezpośredni, tak jak jest możliwy pomiar natężenia pola elektrycznego lub indukcji magnetycznej fali elektromagnetycznej. Amplitudę funkcji falowej możemy poznać jedynie pośrednio poprzez wielkości dopiero od niej pochodzące, takie jak prawdopodobieństwa lub wartości własne. Jedynym wyjątkiem jest λ - długość funkcji falowej, którą można zmierzyć w doświadczeniach dyfrakcyjno-interferencyjnych. Reasumując, chcąc przybliżyć funkcję falową młodemu czytelnikowi nie możemy postępować standardową metodą.

2. Czy istnieje klasyczny analog funkcji falowej?

Prawidłowe rozumienie pojęcia funkcji falowej, zwanej też wektorem stanu, jest niezwykle ważne dla zrozumienia mechaniki kwantowej, ponieważ jest ono fundamentalnym pojęciem tej gałęzi fizyki. Jednak z jednej strony sprawia ono podczas studiowania teorii mikroświata istotną trudność, a to dlatego, że teorie klasyczne nie posiadają jej odpowiednika. Z drugiej strony byłoby bardzo niepożądanym, aby ta teoria była postrzegana jako tylko czysty matematyczny formalizm.

Badając to zagadnienie doszedłem do wniosku, że wprawdzie czystego analogu funkcji falowej nie da się istotnie w mechanice klasycznej wprowadzić, ale można w niej wprowadzić pojęcie prawdopodobieństwa znalezienia samego ciała fizycznego. A tego pojęcia nie wprowadzono, można się jedynie domyślać, że nie dostrzeżono takiej potrzeby. Moim zdaniem taka potrzeba jest i postaram się ją zaspokoić.

Mechanika klasyczna korzysta z pojęcia ciała fizycznego. W jej sformułowaniu ciało fizyczne, jeżeli to tylko możliwe jest sprowadzone do postaci punktu materialnego, którego jedynymi cechami fizycznymi są masa i ładunek elektryczny.

W tym miejscu muszę czytelnikowi uświadomić, że mimo szerokiego używania pojęcia ciała fizycznego w tekstach fizycznych, to jednak to pojęcie w ogóle nie występuje w formalizmie (wzorach) mechaniki klasycznej. Weźmy pod uwagę II zasadę dynamiki Newtona i słynny wzór

F = ma. (1)

Brak jest w tym równaniu jakiegokolwiek odniesienia do pojęcia samego ciała fizycznego, bowiem masa występuje tu samoistnie. Dlatego najpierw spróbujmy wprowadzić samo ciało fizyczne do formalizmu fizyki.

Zauważmy, że ciało fizyczne jest, jeśli istnieje. A zatem wprowadźmy pojęcie funkcji P_kl która będzie stwierdzać fakt istnienia ciała. Będzie to po prostu prawdopodobieństwo znalezienia ciała w konkretnym punkcie r, w danej chwili t.

Koniecznym jest w tym miejscu uzmysłowienie czytelnikowi, że w mechanice klasycznej zakłada się, że ciało fizyczne w danej chwili t może się znajdować tylko w jednym miejscu. Na poziomie szkolnym nic się o tym nie mówi, jest to tam założone w sposób domyślny.

Jest to obserwacja słuszna dla ciał makroskopowych, która w mikroświecie nie musi być spełniona.

Matematycznie wyraża się to przez żądanie, aby funkcja promienia wodzącego ciała fizycznego r(t) była jednoznaczna (a ponadto żąda się jej ciągłości i różniczkowalności co najmniej dwukrotnie). Helmholtz zwrócił uwagę, że te matematyczne założenia mają tu jak najbardziej fizyczny charakter. Chodzi oto, aby ten formalizm opisywał tylko ruchy obserwowalne w przyrodzie.

Nie zdawano sobie wówczas sprawy z tego, że w mikroświecie może być inaczej i pojęcie funkcji promienia wodzącego z tymi założeniami będzie tam bezużyteczne.

W tej sytuacji nasza funkcja P_kl, aby poprawnie opisywać ruch punktu materialnego musi przyjmować wartość 1 w tym punkcie, w którym się on aktualnie znajduje, a w pozostałych 0. Zatem jest to podróżująca wraz z ciałem "jedynka", rys.1.

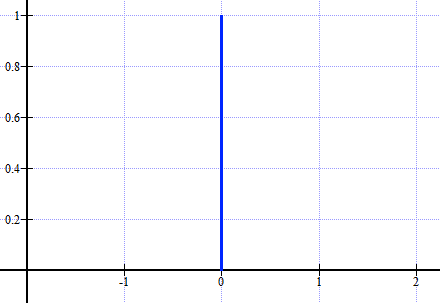
Rys.1 Wykres funkcji P_kl

Z matematycznego punktu widzenia funkcja ta ma szereg niedobrych własności, a mianowicie:

1. 1) jest nieciągła w punkcie położenia ciała,
2. 2) jest również w tym punkcie nieróżniczkowalna.

Czasami w elektrodynamice używa się podobnej funkcji zwanej deltą Diraca do zapisania gęstości ładunku elektrycznego dla punktowego obiektu takiego jak elektron.

Niemniej jednak funkcja P_kl stwierdza, że nasze ciało istnieje oraz podobnie jak położenie r(t) określa, w którym miejscu się ono znajduje. Funkcje takie możemy przypisać każdemu ciału, ponumerować tym samym indeksem co i masę, położenie, czas itd. dla danego ciała. Myślę, że wprowadzenie tego brakującego elementu powinno czytelnikowi pomóc zrozumieć czym jest funkcja falowa.

Chodzi mi bowiem o wprowadzenie pewnych pojęciowych ram wspólnych dla mechaniki klasycznej i kwantowej, tak aby czytelnik zrozumiał, że z formalnego punktu widzenia nie ma powodów, aby z góry odrzucać możliwość, że ciało fizyczne może się znajdować w danej chwili w więcej niż jednym punkcie, a tym samym, że bardziej ogólnym i bardziej adekwatnym pojęciem niż funkcja promienia wodzącego potrzebnym do opisu materii jest pojęcie prawdopodobieństwa znalezienia ciała fizycznego w danym punkcie i w danej chwili.

3. Funkcja falowa w mechanice kwantowej

Teraz analogicznie do funkcji P_kl w mechanice klasycznej wprowadźmy w fizyce kwantowej funkcję określoną jako P_kw. Jej interpretacja ma być podobna. Będzie ona stwierdzać fakt istnienia materii, tak będzie bezpieczniej.

W fizyce kwantowej, a wynika to z wielu doświadczeń, nie da się utrzymać założenia, że ciało fizyczne o mikroskopowych rozmiarach może istnieć w danej chwili tylko w jednym miejscu.

Obiekty mikroświata, takie jak elektrony są nierozróżnialne, a zatem na ogół nie można ich indywidualnie śledzić. Spowodowało to, że musiano tu zrezygnować z pojęcia położenia ciała w czysto klasycznym rozumieniu. Nie nastąpiło to od razu, ale w ciągu długiego okresu, pełnego wątpliwości co do słuszności postulowania nowych kwantowych wielkości fizycznych.

Dlatego moim zdaniem powinno się mówić, że funkcja P_kw reprezentuje fakt istnienia materii, a nie jednego konkretnego ciała fizycznego. Tym samym funkcja P_kw nie może być na ogół podróżującą wraz w ciałem jedynką. Natomiast może to być następująca funkcja rys. 2.

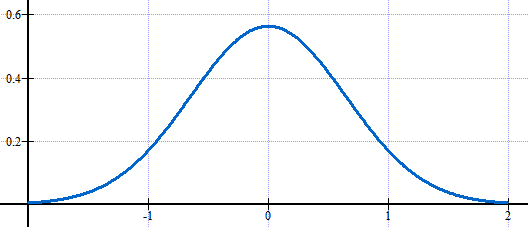
Rys.2 Wykres funkcji P_kw

Funkcja ta mówi nam, że materia przynależna np. do elektronu może występować z niezerowym prawdopodobieństwem w pewnym przedziale położenia. Jednocześnie przy pomocy tej funkcji nie da się stwierdzić, czy w danym miejscu jest tylko kawałek elektronu, czy też elektron jest w tylu miejscach jednocześnie na raz. Współczesne metody badawcze nie są w stanie w ogóle tego zweryfikować. Po prostu nie wiemy, co konkretnie dzieje się z obiektami mikroświata. To jest fakt doświadczalny, z którym póki co musimy się pogodzić.

Natomiast jeden fakt wydaje się oczywisty. Jest to żądanie, aby dany elektron w ogóle się gdzieś znajdował. Oznacza to, że sumując składowe prawdopodobieństwa znajdowania się elektronu w kolejnych miejscach musimy dostać pewność, czyli jedynkę. Matematycznie wyraża się to, w przypadku gdy funkcja P_kw jest całkowalna, poniższym wzorem

∫ P_kw(x)dx = 1 . (2)

Jednak funkcja P_kw różni się zasadniczo od funkcji P_kl, tu analogie klasyczno-kwantowe kończą się.

Po pierwsze P_kw jest funkcją złożoną, tzn. oblicza się ją z innej funkcji, a tę funkcję z kolei wylicza się rozwiązując specjalne równania. Natomiast funkcję P_kl znamy z doświadczenia, nie jest tu potrzebne rozwiązywanie jakiegokolwiek równania.

Po drugie, funkcja z której wylicza się P_kw służy również do obliczania wielkości fizycznych takich, jak pęd czy energia. Z funkcji P_kl nie wylicza się żadnych wielkości fizycznych, służą do tego zasady dynamiki Newtona.

Zatem czas na przedstawienie bohaterki tego artykułu.

W mechanice kwantowej funkcję P_kw wylicza się za pomocą funkcji falowej Ψ(x). Jej pojęcie do fizyki wprowadził Louis de Broglie. Początkowo funkcja ta służyła do obliczania pędu, energii oraz efektów dyfrakcyjno-interferencyjnych cząstek kwantowych i nie posiadała fizycznej interpretacji. P_kw wylicza się z niej następująco

P_kw(x) = Ψ(x)Ψ^*(x). (3)

Ψ(x) jest na ogół funkcją zespoloną, choć nie zawsze tak jest. Zależy to od konkretnej (!) sytuacji fizycznej.

Najważniejszym powodem wprowadzenia tej funkcji była konieczność fizycznego opisu własności falowych materii, które zaczęto obserwować⁽¹⁾. Stało się wtedy jasne, że do opisu wielkości fizycznych w świecie mikroskopowym nie można stosować zasad mechaniki klasycznej, a sama mechanika klasyczna to makroskopowe przybliżenie innej teorii. Drogą badań teoretycznych i doświadczalnych ustalono, że wielkości mechaniczne związane z ciałem fizycznym są powiązane z jego funkcją falową. Dlatego równania na funkcję falową zastąpiły zasady mechaniki Newtona.

Nazwano je równaniami kwantowymi, z których najszerzej stosowane to równanie Schrödingera oraz Diraca. Nie będziemy ich tutaj przytaczać, gdyż są to już stosunkowo skomplikowane równania. Rozwiązanie ich dostarcza postać funkcjonalną funkcji falowej w danym zagadnieniu fizycznym.

Jeżeli tak otrzymana funkcja falowa spełnia poniższe równania (zakładając, że obiekt kwantowy porusza się tylko wzdłuż osi x)

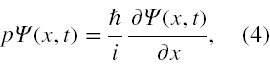
oraz

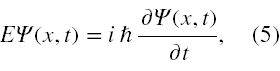
gdzie p i E są wartościami liczbowymi (a nie funkcjami), to można tych równań użyć bezpośrednio do obliczenia pędu i energii tego obiektu (ciała fizycznego). Tu ħ oznacza stałą Plancka podzieloną przez 2π, tj. stałą nazywaną h kreślone.

O ile powiązanie wielkości fizycznych, takich jak pęd i energia ciała z jego funkcją falową nie budziło zastrzeżeń, to interpretacja samej Ψ(x) budziła szereg wątpliwości, a nawet emocji. Minęło sporo czasu zanim przyjęła się statystyczna interpretacja Ψ(x) oparta na przypisaniu funkcji P_kw wartości prawdopodobieństwa znalezienia materii w danym punkcie, pochodząca od Maxa Borna podana powyżej. A i potem byli, a nawet nadal są przeciwnicy tej interpretacji.

4. Podsumowanie

Czas na wnioski.

a) Funkcja falowa Ψ(x) poprzez funkcję P_kw wyraża fakt istnienia materii, natomiast niekoniecznie pojedynczych ciał fizycznych (czasami może się zdarzyć, że materia sprowadza się do jednego ciała np. elektronu, ale w fizyce kwantowej to naprawdę rzadkość!). W mikroświecie bardzo trudno jest śledzić zachowanie pojedynczych obiektów kwantowych, jest to na ogół niewykonalne.

b) Funkcja P_kw wyraża prawdopodobieństwo znalezienia materii (a zatem i ciała fizycznego). Na ogół przyjmuje ona wartości niezerowe na przeważnie dość dużej przestrzeni. Jest to przeciwnie niż w mechanice klasycznej, gdzie nawet rozciągłe ciała fizyczne o dość dużych rozmiarach w opisie fizycznym często można reprezentować punktem materialnym. Tam funkcja P_kl przyjmuje wartość niezerową tylko w jednym punkcie.

c) Funkcja falowa służy do obliczania wielkości fizycznych związanych z materią. Natomiast funkcja P_kl nie służy do obliczania jakichkolwiek wielkości.

d) Funkcja falowa musi posiadać dobre własności takie, jak ciągłość, różniczkowalność, całkowalność w kwadracie. Tym samym pierwsze z dwóch powyższych własności również posiada P_kw. P_kl przeciwnie, nie posiada takich własności i posiadać ich nie musi.

Rekapitulując uważam, że gdyby nie logiczna luka w mechanice klasycznej wskazana przeze mnie na wstępie, to zrozumienie czym jest funkcja falowa byłoby o wiele łatwiejsze.

Moim zdaniem każda mechanika ciał fizycznych musi zawierać formalną możliwość fizycznego opisu, tak na wszelki wypadek, sytuacji gdy ciało fizyczne może się znajdować w danej chwili w więcej niż jednym punkcie położenia, chociaż być może tego dotychczas nie obserwowano, albo po prostu na razie tylko wydaje się, że tego nie zaobserwowano.

(¹) Faktycznie rzeczywiste powody wprowadzenia pojęcia funkcji falowej do fizyki przez Louisa de Broglie'a były trochę inne. Zauważył on, że skoro fale elektromagnetyczne oprócz własności falowych mają też niepodważalne, nowo odkryte własności korpuskularne, to skoro wierzymy w jedność przyrody czyli, że prawa fizyki nie powinny zbytnio różnicować własności pól oddziaływań i materii, zatem materia powinna też wykazywać własności falowe. Ponieważ własności falowe dla materii się wkrótce potwierdziły, więc powyżej użyte skrótowe uzasadnienie jest jak najbardziej usprawiedliwione.