W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 15

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: środa, 16, listopad 2015 22:55

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 2.62, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

Koło toczy się bez poślizgu po drodze z prędkością v = 2 m/s. Oblicz wartość prędkości punktów A i B znajdujących się na obwodzie koła (rys. 2.19). Naszkicuj tor każdego z punktów.

Rozwiązanie

Jeśli chodzi o zdarzenia z życia codziennego, to z pewnością znakomita większość z Was potrafiłaby rozpoznać, kiedy mamy do czynienia z sytuacją, gdy koło (np. samochodu) toczy się bez poślizgu, a kiedy z poślizgiem.

Jednak, jeśli mamy dokonać rozróżnienia takich sytuacji przez podanie warunku wyrażonego językiem fizyki, to sytuacja nie jest już chyba tak oczywista.

Aby pokonać tę trudność spróbujmy opisać na początek (sądzę, że to będzie łatwiejsze) sytuację, kiedy mamy do czynienia z całkowitym poślizgiem.

Powinno chyba nie ulegać wątpliwości, że taka sytuacja ma miejsce, gdy koło się obraca z pewną prędkością kątową ω (załóżmy dla prostoty, że jest ona stała w czasie), a mimo to stoi w miejscu. Przyjmijmy, że taka sytuacja zachodzi na poniższym rysunku nr 1, w chwili czasu t₀.

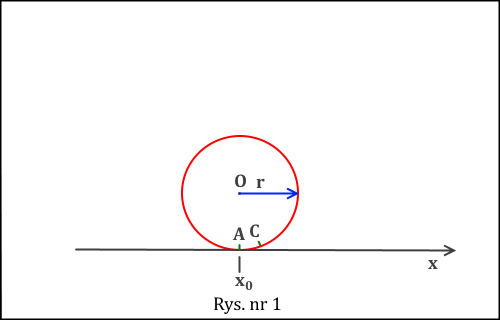
Dla tej chwili czasu punkt A, leżący na obwodzie koła, jak i środek koła O mają współrzędną x położenia identyczną i równą x₀. Chwilę później taką współrzędną x będzie miał inny punkt na obwodzie koła, punkt C. Natomiast współrzędna x środka koła będzie dalej ta sama. I to jest istota poślizgu koła wyrażona językiem fizyki.

Przejdźmy teraz do sytuacji całkowicie przeciwnej i zastanówmy się na czym zatem polega ruch koła bez poślizgu?

Po pierwsze zwróćmy uwagę na to, że przy pełnym poślizgu, po pełnym obrocie koła punkt A znowu powróci do położenia x₀. Postawmy stąd jako pomocnicze pytanie, gdzie będzie punkt A obwodu koła przy braku poślizgu po jednym pełnym obrocie koła?

Brak poślizgu można sobie wyobrazić jako pełne odkładanie się obwodu koła na drodze. Zatem po pełnym obrocie punkt A będzie się znajdował w położeniu x₀ + 2πr.

Aby odpowiedzieć na pytanie, gdzie w tym czasie będzie środek koła O w wyobraźni rozetnijmy obwód koła w punkcie A i odłużmy go wzdłuż osi x, od punktu x₀. Ponieważ środek koła zawsze leży na prostej prostopadłej do stycznej koła i przechodzącej przez punkt styku koła z tą styczną (tą styczną u nas jest oś x), zatem środek koła w czasie toczenia się kolejno będzie znajdował się w każdym położeniu na odcinku od x₀ do x₀ + 2πr. Tym samym środek koła, jeżeli chodzi o położenie na osi x, także przemieści się do punktu x₀ + 2πr.

Powyższe możemy podsumować w formie następujących stwierdzeń.

1. "Koło toczy się bez poślizgu..."

   Oznacza to tylko to, że koło tocząc się po drodze odkłada swój obwód na drodze, a środek koła pokonuje tę samą drogę.

2. Koło toczy się (...) po drodze z prędkością v = 2m/s.

   Oznacza to, że (tak jak pokazano na rysunku nr 2.19) środek koła porusza się ruchem jednostajnym prostoliniowym z prędkością v = 2m/s. Środek tego koła jest jedynym jego miejscem, które nie wykonuje ruchu obrotowego (skutkującego zmianą położenia tego miejsca), a mimo to porusza się.

Zatem dokładne spojrzenie na ruch koła bez poślizgu skutkuje wnioskiem, że jego ruch jest złożeniem dwóch ruchów:

1. ruchu postępowego całego koła z prędkością v = 2m/s, oraz
2. ruchu obrotowego koła wokół jego środka z taką prędkością obrotową, że nie ma poślizgu.

Przechodząc do obliczeń oznaczmy jako T okres obrotu koła. Gdyby koło się nie obracało, to oznaczałoby, że każdy element koła w ciągu czasu T pokonałby drogę

s' = T·v .

Ponieważ koło obraca się bez poślizgu, to każdy punkt na jego obwodzie w ciągu tego okresu T wykona drogę równą

s'' = 2πr,

gdzie r - promień koła.

Jak już wskazałem brak poślizgu oznacza równość obu dróg

s' = s'' ,

a zatem prędkość liniowa ruchu obrotowego miejsc na obwodzie koła jest równa prędkości ruchu postępowego koła

v_l = (2πr)/ T = v_p .

To już wystarczy do udzielenia odpowiedzi.

1) Punkt A, a dokładniej miejsce koła chwilowo znajdujące się w punkcie A, ma dwie prędkości:

̶

prędkość ruchu postępowego identyczną co do wartości, zwrotu i kierunku co środek koła, oraz

̶

prędkość styczną do obwodu koła w tym punkcie (wynikającą z jego ruchu obrotowego) o identycznej wartości i kierunku, ale przeciwnym zwrocie do ruchu postępowego koła.

Dlatego punkt koła, gdy znajduje się w miejscu A ma chwilową prędkość równą 0m/s.

2) Punkt B, a dokładnie miejsce koła tam się znajdujące, ma prędkość styczną do obwodu koła różniącą się tylko przeciwnym zwrotem w stosunku do punktu A. Przy niezmienionym wektorze prędkości ruchu postępowego daje to w wyniku chwilową prędkość równą 2v = 4m/s.

Jak widzisz nie są tu potrzebne jakieś poważne obliczenia, lecz istotna jest praca wyobraźni. Jeśli zaś chodzi o naszkicowanie toru każdego z punktów, to polecam » animację.