Rachunek różniczkowy i całkowy w fizyce szkolnej - część 6

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: czwartek, 18, maj 2015 18:25

Autor : Janusz Szcząchor

Zadanie 3.59, B.Mendel, J.Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

Okienna stora o ciężarze P = 10 N i długości l = 2 m jest nawijana na cienki pręt u góry okna. Jaka praca zostaje wykonana przy zwijaniu story? Opory ruchu można pominąć. Zadanie rozwiąż wykorzystując rachunek całkowy.

Rozwiązanie

Okienna stora to nic innego jak, mówiąc językiem geometrii, prostokątny kawałek materiału o pewnej grubości wiszący przy oknie. Praca jaką wykonujemy przy zwijaniu story (pomijając opory ruchu) akumuluje się w formie przyrostu energii potencjalnej tego przedmiotu. Dlatego możemy po prostu policzyć ten przyrost energii zamiast zastanawiać się jak policzyć pracę.

Jeżeli potniemy w wyobraźni storę na poziome bardzo wąskie paski, to z pewnością zgodzisz się, że wszystkie fragmenty takiego paska uzyskują ten sam przyrost energii potencjalnej. Dzięki temu możemy symbolicznie zwinąć storę w zakresie jej szerokości i grubości oraz rozpatrywać ją symbolicznie jako sznurek. W ten sposób w obliczeniach nie musimy używać parametru szerokości i grubości story, a możemy posłużyć się gęstością liniową przedmiotu zamiast normalnej gęstości objętościowej.

Po tych wyjaśnieniach możemy przejść do obliczeń. Wprowadźmy zatem gęstość liniową story zdefiniowaną jako

ρ_l = m/l , (1)

gdzie l - to długość story, a m - to jej masa dana oczywiście jako

m =P/g , (2)

gdzie tym razem P - to ciężar story, a g - przyspieszenie ziemskie. Ostatecznie wstawiając (2) do (1) otrzymujemy liniową gęstość story wyrażoną przez dane zadania

ρ_l = P/gl . (3)

Wyróżnijmy teraz infinitezymalny (tj. nieskończenie cienki) fragment story o długości dy (patrz niżej rysunek nr 1) i policzmy jego masę. W tym celu odwróćmy wzór (1), aby otrzymać wzór na masę, czyli

m = ρ_l l . (4)

Zauważmy, że we wzorze (4) l to nie tyle zmienna, co raczej różnica (odległość) między dwoma położeniami na zmiennej y [1]. Dlatego różniczkując stronami (4) możemy zapisać

dm = ρ_l dy . (5)

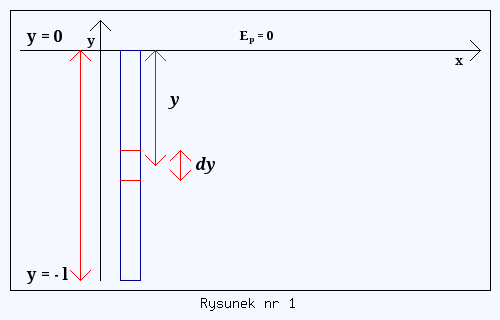
Z kolei obliczmy ile wynosi przyrost energii potencjalnej takiego fragmentu masy dm podczas jego podnoszenia od miejsca jego położenia do poziomu y = 0.

Wybierzmy poziom zera energii potencjalnej właśnie na poziomie pręta u góry okna (patrz rysunek nr 1), w miejscu gdzie y = 0. Wtedy fragmenty story przed podniesieniem mają potencjalną energię o wartości ujemnej.

Nasz wyróżniony fragment znajduje się w odległości y od miejsca, gdzie znajduje pręt, na który zwijamy storę. Wtedy przyrost energii potencjalnej takiego fragmentu będzie równy energii jaką ten fragment posiada przed podniesieniem wziętej ze znakiem minus, czyli

dE_p = - gydm , (6)

ponieważ na ten fragment masy dm działa siła grawitacji gdm i znajduje się on na wysokości y poniżej poziomu zera energii potencjalnej [2]. W końcu podstawiając (5) do (6) otrzymujemy

dE_p = - (P/l)ydy . (7)

Całkowity przyrost energii potencjalnej story uzyskamy całkując dE_p po wszystkich możliwych położeniach y fragmentów story. W ten sposób wysumujemy przyrosty energii potencjalnej wszystkich jej fragmentów. Stora rozciąga się od położenia y = - l, do y = 0. Zatem całkowity przyrost energii potencjalnej story dany jest całką (dla podkreślenia faktu, że jest to przyrost wynik oznaczyłem z użyciem znaku Δ)

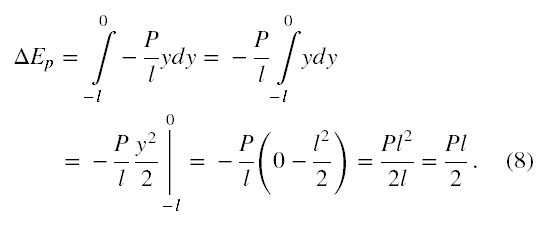
I tyle też wynosi praca wykonana przy nawijaniu story.

Wynik możnaby otrzymać bez odwoływania się do pojęcia energii potencjalnej. Jednak uznałem, że z dydaktycznego punktu widzenia łatwiej mi będzie wyjaśnić dlaczego całkujemy energie potencjalne fragmentów story niż dlaczego musimy całkować pracę wykonaną wzdłuż osi y związaną z podnoszeniem jej fragmentów ponownie po tej samej osi y. Obawiałem się, że osoba zaczynająca stosowanie rachunku całkowego w fizyce mogłaby w tym punkcie rozumowania doznać lekkiego chaosu pojęciowego.

Przypisy

[1] Faktycznie długość naszego ciała l, aby wyrażała odległość i była jednocześnie zmienną można zapisać jako

l = y - y₀, (i)

gdzie y₀, to pewna stała. W tym zadaniu akurat równa - l, bo tam, gdzie l = 0, tam y = - l. Teraz różniczkując stronami (i) otrzymujemy, że

dl = dy,

co wyjaśnia całkowicie wzór (5).

[2] Jeżeli masz wątpliwości co do słuszności takiego postępowania to śpieszę Ci przypomnieć, że wzór na energię potencjalną w polu grawitacyjnym wynika ze wzoru na pracę. Zwykle jest tak, że poziom zera tej energii przyjmuje się tam, gdzie ciało spoczywa. Wtedy dodatnia praca (przeciwko sile pola grawitacyjnego) skutkuje dodatnią wartością tej energii. Jeżeli przeniesiemy poziom zera energii tak jak tutaj, to przyrost energii też jest dodatni, ale gdy ciało osiąga wartość zerową tej energii po jego podniesieniu, to przed podniesieniem ma taką energię jaką wykona się pracę ze znakiem minus.