Rachunek różniczkowy i całkowy w fizyce szkolnej - część 8

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: wtorek, 18 sierpień 2015 14:20

Autor : Janusz Szcząchor

Zadanie J.Szcząchor i R.Resnick, D.Halliday - "Fizyka dla studentów nauk przyrodniczych i technicznych - Tom I", PWN, Warszawa 1973

Wyprowadź wzór na moment bezwładności pełnego walca względem jego głównej osi w ten sposób, że najpierw oblicz jego energię kinetyczną w ruchu obrotowym. Zakładamy, że rozkład masy w walcu jest jednorodny. Zrób to samo dla rury cylindrycznej, gdzie R₁ to jej promień wewnętrzny, a R₂ zewnętrzny. W obu przypadkach zakładamy, że ciało obraca się ze stałą prędkością kątową ω.

Rozwiązanie

Energia kinetyczna punktu materialnego jest dana wzorem

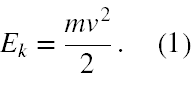
Traktując ciało sztywne typu walec, rura jako zespół, nawet nieskończonej liczby punktów materialnych możemy obliczyć jego energię kinetyczną sumując energie kinetyczne wszystkich takich punktów. Nie ma to znaczenia czy mówimy o ruchu postępowym, czy obrotowym ciała sztywnego. Spróbujemy więc rozwiązać to zadanie tą metodą.

Przystępujemy zatem do podzielenia pełnego walca na punkty materialne. Jak to zrobić (patrz rysunek nr 1)?

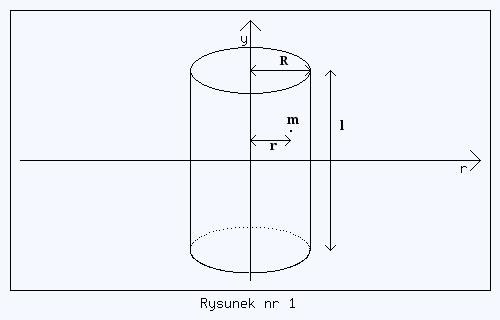
Formalnie mamy pełną swobodę w podziale walca, ale z uwagi na to, aby obliczenia matematyczne dały się faktycznie wykonać tak dobrze nie jest. Nie możemy przecież sumować energii kinetycznych na piechotę. Z uwagi na ciągły rozkład masy w walcu musimy użyć rachunku całkowego i dlatego należy walec pociąć na odpowiednio małe elementy oraz takiego kształtu, aby dało się wykonać potrzebną całkę.

Po pierwsze zwróćmy uwagę, że w ruchu obrotowym ze stałą prędkością zachodzi zależność v = ωr, zatem wzór (1) przechodzi w

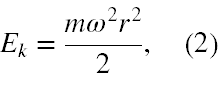
gdzie r - bieżąca odległość punktu materialnego od osi obrotu, m - masa tego punktu materialnego, a ω - to prędkość kątowa walca.

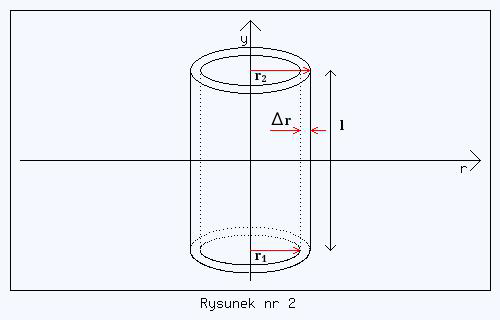
Przyglądając się naszemu walcowi widzimy, że naturalnym jest pocięcie go na bardzo cienkie warstwy walcowe o tak małej grubości, że wszystkie elementy takiej warstwy są w tej samej odległości r od osi obrotu (porównaj rysunki nr 1 i nr 2). Dzięki takiemu zabiegowi energię kinetyczną takiej cienkiej warstwy walcowej będziemy mogli nadal wyrażać wzorem (2), bo suma energii kinetycznych wszystkich elementarnych mas takiej warstwy da się wyrazić przez

∑i E_k(m_i) = ∑i(m_iω²r²/2) = (∑im_i)ω²r²/2.

Zauważmy z kolei, że gdy zwiększamy r, to rośnie objętość takiej warstwy. Zatem, z uwagi na jednorodność walca (stałość gęstości) poszczególne takie warstwy różnią się masą. Stąd we wzorze (2) zastosowanym do cienkiej warstwy walcowej masa m jest funkcją zmiennej r.

W tym miejscu musimy zastanowić się jakie wielkości w naszych rachunkach będziemy uważać za dane zadania. Mamy już jedną daną, jest to ω. Co dalej?

Walec jest jednorodny, ma stałą gęstość. Czy kolejną daną powinno być ρ? Niekoniecznie. Zauważ, że ostatecznie chcemy otrzymać wzór na moment bezwładności! We wzorach na moment bezwładności nie używa się gęstości, a np. masy. Zatem jako kolejną daną przyjmiemy masę walca i oznaczymy ją jako M.

Powinieneś znać wzór na objętość walca →V = πR²l, gdzie R i l to zmienne wskazane na rys. nr 1, a zatem gęstość jednorodnego walca powinna być dana jako

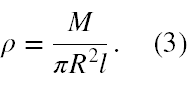
Zauważ, że R - promień walca, to kolejna dana tego zadania. Ustaliwszy to przechodzimy do dalszych obliczeń.

Interesująca nas warstwa walcowa to nic innego jak prostokąt o szerokości 2πr (obwód koła) i wysokości l (wysokość walca) zwinięty w rulon. Ile wynosi jej grubość? Jak zobaczysz niżej, grubość takiej warstwy to jeden z podstawowych chwytów przy układaniu wzoru na różniczkę w tego typu zadaniach.

Przypomnijmy, mamy wysumować energię kinetyczną warstw walcowych w ruchu obrotowym, aby otrzymać wzór na takową dla pełnego walca. Matematycznie oznacza to, że musimy scałkować różniczkę dE_k energii kinetycznej. Z uwagi na wzór na energię (2), który pokazuje, że E_k jest funkcją kilku zmiennych i parametrów, taka różniczka będzie musiała się wyrażać jako pochodna pewnej funkcji względem zmiennej niezależnej razy różniczka tejże zmiennej niezależnej.

Ponadto trzeba zauważyć, że sumowanie energii kinetycznych po warstwach walcowych musi pośrednio prowadzić do zsumowania ich mas, bo interesuje nas energia kinetyczna całej masy walca. Dlatego przed przystąpieniem do całkowania musimy wzór (2) przekształcić w

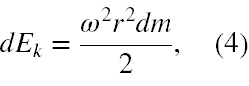
bo tylko różniczkowa ilość masy może posiadać różniczkową ilość energii kinetycznej.

Jednak w tym miejscu muszę zaznaczyć, że to zależy od konkretnej sytuacji zadaniowej (i fizycznej) jaki jest schemat zależności różniczki, którą całkujemy od zmiennej niezależnej. Nie ma tu żadnego schematyzmu, ani jednoznacznego przepisu. Za każdym razem trzeba wszechstronnie analizować sytuację fizyczną.

Powyżej już wskazałem, że masa warstwy walcowej zależy od r i teraz czas ustalić jak różniczka dm zależy od tej zmiennej. Zauważ, że grubość warstwy walcowej (patrz rysunek nr 2) to przedział między wartością promienia r₁ → wewnętrznego, a wartością promienia zewnętrznego → r₂, czyli grubość ta to

Δr = r₂ - r₁ .

Zbliżając r₁ do r₂ (lub na odwrót) otrzymujemy coraz cieńszą warstwę, aż jest tak cienka, że w każdym jej miejscu jej odległość od osi obrotu jest równa r . Taką infinitezymalną grubość oznaczamy jako dr (formalnie zamieniamy Δ na d), bo jest to odległość jakby nie było wzdłuż zmiennej r. Stąd objętość takiej cieniutkiej warstwy walcowej to nic innego jak

dV = 2πrldr,

bo tylko różniczkowa objętość może mieć różniczkową grubość. Teraz różniczkę masy cienkiej warstwy walcowej dm w (4) możemy wyrazić jako iloczyn różniczkowej objętości dV i gęstości walca ρ ze wzoru (3). I w końcu, upraszczając πl otrzymujemy

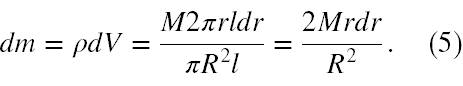
Na koniec wstawiając (5) do (4) otrzymujemy upragniony wzór na różniczkę energii kinetycznej zapisaną specjalnie w trochę dziwnej formie, czyli

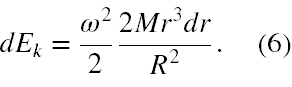
Ze wzoru (6) widać, że można wyłączyć wyrażenie ω²/2. Stąd zgodnie z definicją energii kinetycznej dla ruchu obrotowego

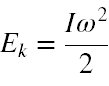
widzimy, że różniczka momentu bezwładności cienkiej warstwy walcowej, to

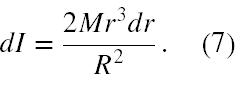
1. Jeżeli chcemy otrzymać moment bezwładności pełnego walca, to musimy wycałkować (7) w granicach od 0 do R.
2. Z kolei, aby otrzymać moment bezwładności rury, to musimy zmienić wyrażenie na gęstość ρ. Objętość rury, to V = πl [(R₂)² - (R₁)²], a zatem gęstość rury ma teraz formę

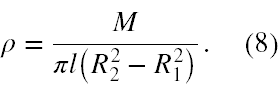
Stąd wzór (7) na dI zmienia swoją postać na

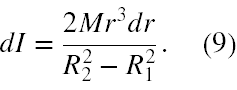
Policzymy moment bezwładności rury. A więc

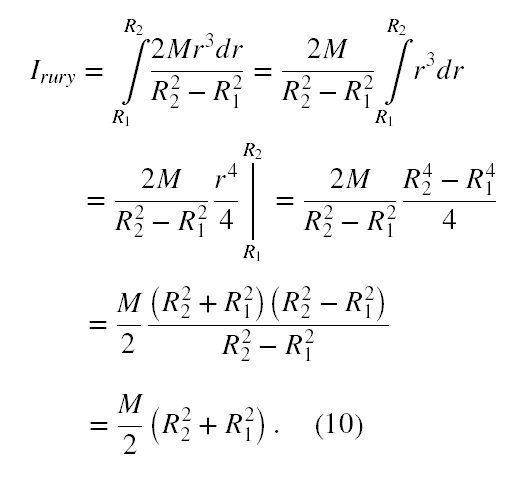
Moment bezwładności pełnego walca powinieneś policzyć sam, nie trzeba już nic całkować!