W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 7

Szczegóły
Kategoria: Zadania z fizyki
Opublikowano: wtorek, 27 styczeń 2015 14:20
Autor : Janusz Szcząchor


O mnie:
Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 1.60, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976

W punktach A i B odległych o l = 25 m znajdują się dwa ciała, poruszające się ruchem jednostajnie zmiennym w jednym kierunku po prostej AB. W chwili t0 = 0 ciało A ma prędkość v1 = 1m/s i przyspieszenie a1= 1,16m/s2, a ciało B ma prędkość v2 = 5m/s i przyspieszenie a2= 0,2m/s2. Po jakim czasie ciało A dogoni ciało B?  » Rozwiązanie

zadanie nr 1.63, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Oblicz drogę przebytą przez ciało w czasie Δt = 4s, jeśli prędkość w tym ruchu wyraża się wzorem : v = a + bt, gdzie wartości liczbowe a i b w odpowiednich jednostkach układu SI wynoszą: a = 5, b = 3. Należy przyjąć, że t0 = 0. » Rozwiązanie

Rozwiązanie zadania nr 1.60 1

Sama treść fizyczna w zadaniu jest dość prosta. Ciało A, gdy dogoni ciało B, będzie miało to samo położenie co i B. Zatem droga ciała A będzie równa odległości l plus droga ciała B. Skoro oba ciała poruszają się ruchem jednostajnie przyspieszonym (zmiennym z dodatnim przyspieszeniem), więc mamy następujące równanie na drogę

s1 = l + s2, (1)

v1Δt + a1(Δt)2/2 = l + v2Δt + a2(Δt)2/2. (2)

Przenosimy wszystkie wyrazy na lewą stronę (odpowiednio zmieniając znaki) i mamy

a1(Δt)2/2 - a2(Δt)2/2 + v1Δt - v2Δt - l = 0 . (3)

Musimy obliczyć Δt, a tu Δt występuje w pierwszej, jak i drugiej potędze. Zatem jest to równanie kwadratowe. Wyłączamy za nawiasy (Δt)2, jak i Δt, i otrzymujemy czystą postać równania kwadratowego

[(a1 - a2)/2](Δt)2 + (v1 - v2)Δt - l = 0, (4)

gdzie współczynniki trójmianu kwadratowego to:

a = (a1 - a2)/2,

b = (v1 - v2),

c = - l.

Obliczamy deltę

Δ = b2 - 4ac = (v1 - v2)2 - 4[(a1 - a2)/2](-l).

Aby wiedzieć, czy w ogóle istnieje rozwiązanie naszego równania kwadratowego musimy poznać wartość liczbową delty, a zatem do powyższego podstawiamy wartości dane w zadaniu

Δ = (1m/s - 5m/s)2 + 4(1,16m/s2 - 0,2m/s2)(25m)/2 =
16m2/s2 + 2*0,96*25m2/s2 = 64 m2/s2

Skoro Δ > 0, to mamy dwa rozwiązania! Zatem rozwiązanie na Δt to:

Δt1/2 = ( - b ± √Δ )/2a,

czyli

Δt1/2 = { - (v1 - v2) ± √((v1 - v2)2 + 2l(a1 - a2))}/(a1 - a2) =
(4 m/s ± 8 m/s)/ 0,96m/s2

Wartość ze znakiem minus jest ujemna, a zatem niefizyczna i należy ją odrzucić. Zatem rozwiązaniem jest

Δt = { - (v1 - v2) + √((v1 - v2)2 + 2l(a1 - a2))}/(a1 - a2) = 12,5s.

Rozwiązanie zadania nr 1.63 2

Jest to ten typ zadania, gdzie istotna jest analiza wymiarowa. Skoro prędkość jest dana wzorem v = a + bt to oznacza, że zależy ona od czasu. Zatem w tym ruchu prędkość nie jest stała. Musimy teraz sprawdzić, czy przyspieszenie jest stałe, bo jeśli tak, to będziemy wiedzieli jak rozwiązać zadanie. Na tym etapie nauki fizyki nie możesz inaczej postąpić. Gdybyś znał rachunek całkowy, nie musiałbyś się czymkolwiek martwić. Mógłbyś po prosty scałkować po czasie wzór na prędkość, aby dostać wzór na drogę.

Aby policzyć przyspieszenie konieczne będzie użycie ogólnej jego definicji, bo prędkość jest tu dana funkcją. Przypomnijmy, że przyspieszenie jest ogólnie dane wzorem

definicja przyspieszenia jako granicy ilorazu różnicowego

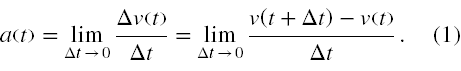
Zgodnie z tą definicją i podaną w zadaniu funkcją prędkości widzimy, że we wzorze na przyspieszenie v jest raz funkcją tylko t, a drugi raz t + Δt. Zatem

obliczenie przyspieszenia

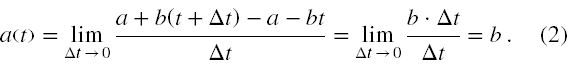
Stąd w tym ruchu przyspieszenie jest stałe.

W zadaniu należy przyjąć, że t0 = 0s. Tym samym prędkość początkowa jest równa a. Dlatego nasze ciało porusza się ruchem jednostajnie przyspieszonym z prędkością początkową a. Zatem wzór na drogę jest nam znany i przyjmując, że v0 = a i a = b mamy

obliczenie drogi

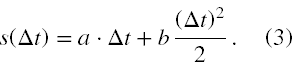
Pamiętając, że a musi mieć wymiar prędkości i b wymiar przyspieszenia powinieneś już być w stanie sam dokończyć obliczenia liczbowe.