O wyprowadzeniu wzoru na wariację bez wariacji czasu funkcji Lagrange'a

Szczegóły

Kategoria: Matematyczne metody Fizyki

Opublikowano:sobota, 23 listopad 2019 22:34

Autor : Janusz Szcząchor

Użycie metod rachunku wariacyjnego w sformułowaniu mechaniki klasycznej, a także mechaniki kwantowej to bardzo ważne zagadnienie. Nie trzeba nikogo chyba przekonywać jak ważne miejsce w fizyce mają zasady Hamiltona, Maupertuis czy Jacobiego. Jednak do ich sformułowania jest potrzebne pojęcie wariacji funkcji, chociażby bez wariacji czasu. I tu moim skromnym zdaniem podręczniki mechaniki dla fizyków zbyt mało poświęcają czasu, aby objaśnić co to właściwie za wielkość. Aby ten brak uzupełnić, odczuwalny bardzo przeze mnie, sięgnąłem do podręczników analizy matematycznej.

W podręczniku Rubinowicza i Królikowskiego [1] na wstępie paragrafu poświęconego zasadzie Hamiltona mamy wprowadzenie pojęcia wariacji funkcji złożonej. Prześledzimy je, ponieważ będzie ono nam potrzebne w przyszłych artykułach, a także przedstawimy szczegółowe wyprowadzenie wzoru na tę wielkość.

Załóżmy, że ruch układu punktów materialnych w przestrzeni konfiguracyjnej dany będzie poprzez zespół zmiennych położeniowych q_l (t), l=1,...,3n. Nazwijmy go ruchem rzeczywistym tego układu i niech ma on miejsce od chwili t₀ z punktu q₀ = q(t₀) do chwili t₁ i punktu q₁ = q(t₁). Niech zmienne położeniowe w rozpatrywanym przedziale czasu mają ciągłe drugie pochodne - rysunek nr 1.

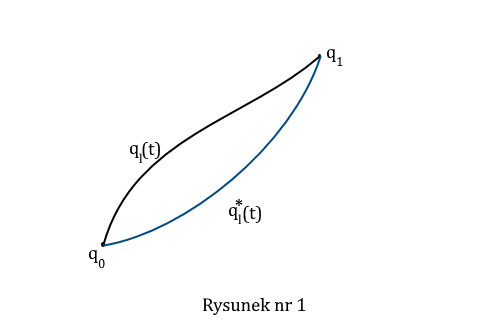
Rozważmy dowolny inny ruch q_l^* (t) (nierzeczywisty), który miałby miejsce między tymi samymi chwilami czasu i tymi samymi punktami położenia początkowym i końcowym, czyli

q_l^* (t₀) = q₀, (1)

q_l^* (t₁) = q₁. (2)

Nazwijmy go ruchem porównawczym zgodnym z więzami. Przy pomocy zmiennych położeniowych ruchu rzeczywistego możemy jego zmienne zapisać jako

q_l^* (t) = q_l (t) + δq_l (t), (3)

gdzie δq_l (t), to wariacja (bez wariacji czasu) współrzędnej uogólnionej q_l (t). O wariacjach tych będziemy zakładać, że mają ciągłe pierwsze pochodne w rozpatrywanym przedziale czasu.

Rozważmy w końcu dowolną funkcję F(q_l(t),q^•_l(t),t) mającą ciągłe drugie pochodne cząstkowe w rozważanym obszarze zmiennych q_l(t), q^•_l(t), t. Utwórzmy dla tej funkcji różnicę jej wartości w ruchu porównawczym i rzeczywistym w tych samych chwilach czasu. I teraz w podręczniku tym, na stronie 203 mamy stwierdzone.

Korzystając ze wzoru Taylora mamy

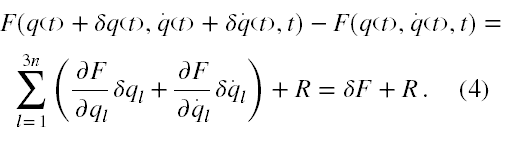
Niestety, ale Ja nie znam takiego wzoru, przynajmniej na poziomie zwykłej analizy matematycznej, bo jak na przykład można to znaleźć (dla pewności) w [2], że rozwijanie w szereg Taylora(-Maclaurina) polega na rozwijaniu funkcji w szereg względem potęg zmiennej niezależnej, a nie funkcji złożonej względem potęg części funkcji wewnętrznej. Aby wyjaśnić jak naprawdę obliczyć wariację funkcji złożonej (i przy jakich założeniach) sięgnąłem do starych, ale naprawdę dobrych podręczników analizy [3] i [4].

Wariację zmiennej uogólnionej należy przedstawić jako

δq_l (t) = αη_l(t), (5)

gdzie funkcja η_l(t) = 0 dla t = t₀ oraz t = t₁, jest klasy C₁, a α jest małym parametrem liczbowym.

Funkcja F jest teraz funkcją q_l (t) + αη_l(t), q^•_l (t) + αη^•_l(t) oraz t, ale także parametru α. Rozwińmy tę funkcję w szereg Taylora względem potęg parametru α w sposób następujący

Iloczyn αF^'(0), to właśnie pierwsza wariacja bez wariacji czasu funkcji F. Policzmy najpierw pochodną funkcji F po α pamiętając, że faktycznie mamy policzyć pochodną funkcji złożonej. Mamy

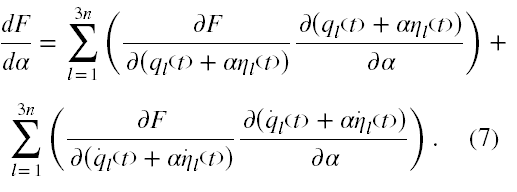
Pochodne po α w iloczynach da się wykonać explicite. Następnie przechodząc z α ⇾ 0 otrzymujemy

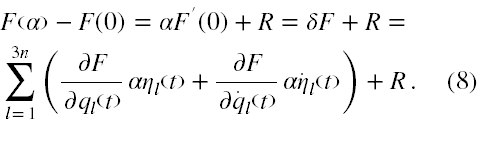
Jeżeli przyjmiemy, że

to mamy udowodniony wzór na wariację bez wariacji czasu funkcji F z podręczników mechaniki klasycznej.

Aby pominąć resztę R w pierwszym przybliżeniu wariacji δF różnicą funkcji F(q_l(t),q^•_l(t),t) w ruchu porównawczym i rzeczywistym istotne jest założenie, że parametr α jest niewiele większy od 0. Wtedy najistotniejszy wkład do różnicy funkcji stanowią wyrazy I rzędu małości α. Wszystkie dalsze wyrazy, zawarte w reszcie R, jako zawierające wyższe potęgi parametru α są wielkościami małymi wyższych rzędów.

Literatura

[1] W.Rubinowicz,W.Królikowski, Mechanika Teoretyczna, Rozdział 2, §14 Zasada Hamiltona, PWN, Warszawa 1978.

[2] W. I. Smirnow, Matematyka wyższa, Tom I, Rozdział IV, §13.126-128, PWN, Warszawa 1958.

[3] W. Pogorzelski, Analiza matematyczna, Tom IV, Część jedenasta, PWN, Warszawa 1956.

[4] W. I. Smirnow, Matematyka wyższa, Tom IV, część pierwsza, Rozdział 2, PWN, Warszawa 1961.