Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 3

Szczegóły

Kategoria: Publikacje naukowe

Opublikowano: piątek, 10 sierpień 2018 18:25

Autor : Janusz Szcząchor

Do we know everything about bound stationary states?

Abstract: Some physical properties of s-states of hydrogen atom are analyzed.

5. Niektóre własności stanów typu s dla atomu wodoru

W rozwoju mechaniki kwantowej bardzo ważną rolę odegrała sformułowana w roku 1923 przez N. Bohra zasada korespondencji [1],§2, §5, §7, §24 oraz [2], Chapter I, IV §12, zgodnie z którą mechanika klasyczna powinna być przypadkiem granicznym mechaniki kwantowej. Jeśli chodzi o jej matematyczne sformułowanie, to często ono przyjmuje postać żądania, aby w granicy ħ → 0, prawa mechaniki kwantowej przechodziły w prawa mechaniki klasycznej, czyli równanie Schrödingera w tej granicy powinno się zredukować do równania Hamiltona-Jacobiego.

Spójrzmy zatem do czego w tej granicy redukuje się dla niezaburzonego atomu wodoru dowolne rozwiązanie równania Schrödingera będące funkcją falową typu s, czyli przypisującą elektronowi wartość własną orbitalnego momentu pędu równą 0? Spojrzenie do teorii Bohra jasno pokazuje, że nie ma takiej klasycznej możliwości, aby w atomie moment pędu elektronu był równy 0.

Naszym zdaniem zasada korespondencji jest niespełnioną hipotezą fizyczną. Przytoczyliśmy ją tu tylko po to, aby uzasadnić jak bardzo ważne dla zrozumienia świata kwantowego jest staranne poznanie własności fizycznych elektronu w tego typu stanach kwantowych, a tym samym temat tej sekcji.

Dyskusję własności stacjonarnych stanów s w atomie wodoru dokonamy na przykładzie stanu 1s, którego zależność od współrzędnych przestrzennych w sferycznym układzie współrzędnych ma następującą postać [3], rozdział 2, §3

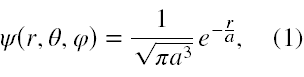
gdzie a jest promieniem bohrowskim danym jako

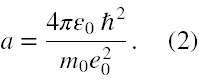
Jeśli chodzi o rozkład gęstości prawdopodobieństwa |ψ(r,θ,φ)|², to taka funkcja ma pełną symetrię sferyczną, a jej zależność od zmiennej r jest przedstawiona na poniższym wykresie (skala na osi y celem poprawy widoczności jest nieproporcjonalna).

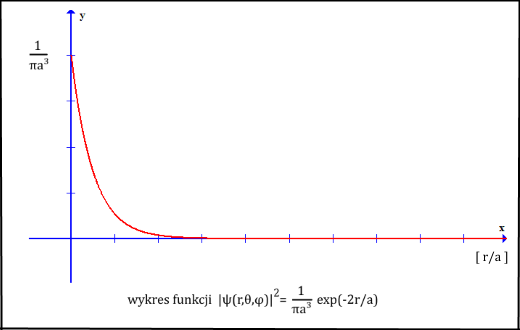
W Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 1 wskazaliśmy, że zgodnie z  modelem Bohra elektron mając moment pędu równy 0 musiałby poruszać się ruchem wahadłowym, tam i z powrotem wzdłuż jednej ze średnic orbity kołowej przez środek jądra atomowego. Taki ruch nie ma symetrii sferycznej. Zatem elektron kwantowy ma wprost niewobrażalną swobodę poruszania się w stosunku do sytuacji klasycznej.

Zbadajmy problem głębiej i obliczmy ile wynosi pęd elektronu w tym stanie kwantowym. Zrobimy, to poprzez obliczenie wartości oczekiwanej operatora pędu w stanie 1s zgodnie z definicją zawartą w [1], §7 (¹),

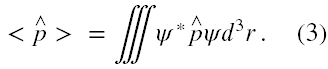
We współrzędnych biegunowych operator ten ma następujące składowe [4],

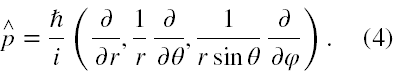
Ponieważ funkcja falowa (1) nie zależy od kątów biegunowych, więc wartości oczekiwane drugiej i trzeciej składowej w (4) są równe 0. Co do wartości pierwszej składowej, to jest ona równa iħ/a, czyli jest urojona. Wartości własne operatorów muszą być rzeczywiste. Aparat mechaniki kwantowej nie wyjaśnia co taka sytuacja może oznaczać. Biorąc pod uwagę, że operator pędu w polu Coulomba nie jest całką ruchu należy uznać, że wartość pędu elektronu w tym stanie jest nieokreślona.

Tak więc mamy zaskakującą sytuację fizyczną. Naszym zdaniem, ruch elektronu w tym stanie kwantowym nie ma nic wspólnego z ruchem w jakimkolwiek sensie klasycznym, w którym tor ruchu jest zawsze krzywą, a pęd jest ciągłą i rzeczywistą funkcją czasu. Jest jeszcze jeden istotny aspekt tego ruchu. Jeżeli opisujemy elektron kwantowo, to gdy znajduje się on w konkretnym stanie (kwantowym), to jego energia nie zależy od jego odległości od jądra atomu. Przeciwnie, niby-klasyczne przebywanie na konkretnej "skwantowanej" orbicie oznacza jego stałą odległość od jądra (²).

Sądzimy, że te argumenty są już na tyle wystarczające, aby zdać sobie jasno sprawę z tego, że jakiekolwiek klasyczne teorie, czy to Bohra, czy to Bohra-Sommerfelda dostarczają absolutnie nieadekwatnego obrazu świata mikroskopowego, którego nie należy brać pod uwagę nawet do rozważań czysto poglądowych.

UWAGI

(¹) Relacje komutacji nie zależą od rodzaju użytych współrzędnych. We współrzędnych prostokątnych łatwo widać, że operator energii kinetycznej (-ħ²/2m)∇² komutuje z operatorem pędu (ħ/i)∇. Operator energii potencjalnej w polu Coulomba w formie -e²/r nie zależy od współrzędnych kątowych, zatem druga i trzecia składowa biegunowa operatora pędu z nim komutują. Jednak pęd radialny nie komutuje z tym operatorem, zatem pęd nie jest całką ruchu w tej sytuacji fizycznej. Stąd operator pędu nie ma tu wartości własnych, możemy tylko spróbować policzyć wartość oczekiwaną tego operatora. Całką ruchu jest tu moment pędu.

(²) Przedstawienia zagadnienia stanów stacjonarnych na przykładzie atomu wodoru z niezrozumiałych powodów pomijają istotny aspekt tego problemu. Zarówno dowód istnienia stanów stacjonarnych oparty na półklasycznym modelu Bohra przedstawiany w szkole średniej, jak i kwantowy dowód oparty na równaniu Schrödingera zwykle wykładany na uniwersytetach w ramach wykładu "Mechanika kwantowa I" dowodzą skwantowania energii całkowitej w atomie.
 W modelu Bohra wprost obliczamy energię całkowitą E = E_k + E_p przy uwzględnieniu warunku kwantowego Bohra.
 W równaniu Schrödingera operator iħ∂/∂t jest operatorem energii całkowitej i to on musi posiadać wartości własne.
 Jednak w obu przypadkach istnieją wyrażenia na energię kinetyczną elektronu. W modelu Bohra jest ona też skwantowana.
 Natomiast w mechanice kwantowej jest ona dana operatorem E_k = iħ∂/∂t + eφ (gdy bierzemy pod uwagę elektron, który ma ładunek ujemny). W dowolnym stanie stacjonarnym byłaby to dobrze określona wartość, gdybyśmy wiedzieli jaką wziąść pod uwagę wartość potencjału skalarnego. Ponieważ "kwantowy" elektron ma swobodę poruszania się po znacznej części atomu (w przeciwieństwie do tylko orbity kołowej dla modelu Bohra), więc nie można wskazać o jaką wartość tego potencjału tu może chodzić. Tym samym elektron "kwantowy" nie ma określonej wartości energii kinetycznej, a tym samym nie ma dowodu, że jest ona skwantowana.

LITERATURA

[1] L. Schiff, Quantum Mechanics, McGraw-Hill, New York, 1968.

[2] A. Messiach, Quantum Mechanics, Volume I, North-Holland Publishing Company, Amsterdam 1961.

[3] J. Ginter, Wstęp do fizyki atomu, cząsteczki i ciała stałego, PWN, Warszawa 1979.

[4] E. Karaskiewicz, Zarys teorii wektorów i tensorów, PWN, Warszawa, 1974.