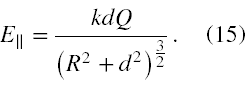Rachunek różniczkowy i całkowy w fizyce szkolnej - część 11

Szczegóły

Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej

Opublikowano: sobota, 27, maj 2017 14:59

Autor : Janusz Szcząchor

zadanie - Janusz Szcząchor, Henryk Kaczorek, Zbigniew Słówko

Na pierścień o promieniu R = 6 cm wykonany z przewodnika o znikomej grubości wprowadzono ładunek Q = 2,5·10^-9 C. Przy pomocy rachunku całkowego znajdź natężenie pola elektrycznego pochodzącego od tego pierścienia w punkcie znajdującym się w odległości d = 8 cm od środka pierścienia na jego osi.

Rozwiązanie

Zadanie to powstało poprzez zaadaptowanie rozwiązanego przykładu 3.1 w H. Kaczorek, Z. Słówko - "Zbiór zadań z fizyki", WSiP, Warszawa 1981. Mimo, że można je rozwiązać bez użycia rachunku całkowego, to z uwagi na prostotę przykładu, z pewnością będzie ono doskonałym ćwiczeniem dla osób początkujących w stosowaniu tego rachunku w fizyce przed przystąpieniem do rozwiązywania dużo bardziej złożonych problemów.

Na początku zauważmy, że z uwagi na to, iż pierścień jest przewodnikiem ustali się na nim jednorodny rozkład ładunku elektrycznego. Ponadto skoro w treści zadania napisano, że ma on znikomą grubość, więc możemy potraktować go jako źrodło pola elektrycznego o liniowej gęstości ładunku równej

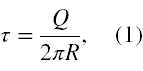
gdzie 2πR, to długość naszego przewodnika.

Na poniższym rysunku jest narysowany szkic sytuacji zadaniowej.

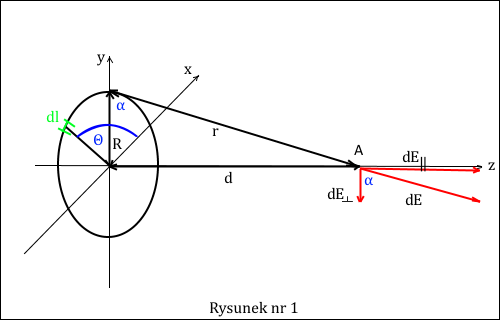
Weźmy teraz pod uwagę różniczkowy element długości pierścienia dl (oznaczony na rysunku na zielono), który jest tak mały, że praktycznie każdy elementarny ładunek elektryczny w nim zawarty daje taki sam wektor natężenia pola elektrycznego w punkcie A. Dzięki temu pola elektryczne pochodzące od tych ładunków można zsumować przez zwykłe dodanie wektorów. Wyrażamy to poprzez napisanie, że w takim elemencie wypadkowym źródłem pola jest różniczkowy ładunek elektryczny o wartości

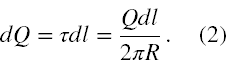
Jednak w układzie współrzędnych biegunowych w płaszczyźnie xy zmienna l to nie jest zmienna niezależna. Zmiennymi niezależnymi są tutaj kąt Θ oraz odległość od środka układu współrzędnych r, która tutaj przyjmuje stałą wartość R (nieszczęśliwie w prawie Coulomba też się stosuje ten sam symbol r dla odległości między ładunkami). W ten sposób korzystając ze wzoru na obwód koła (pod warunkiem, że kąt Θ jest mierzony w radianach) możemy napisać, że

dl = RdΘ. (3)

Dlatego dQ jest równe

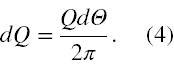
Natężenie pola elektrycznego od takiego ładunku, to też różniczka, czyli dE. Jest ona zgodnie z definicją tej wielkości fizycznej oraz warunkami zadania równa

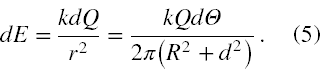
Widzimy z rysunku nr 1, że wektor natężenia pola elektrycznego rozkłada się na składową podłużną dE_∥, równoległą do osi z oraz dE_⊥, poprzeczną do tej osi. Łatwo można zauważyć, że wszystkie składowe poprzeczne dają w sumie wektor zerowy, a wypadkowe pole od całego pierścienia, to suma wszystkich składowych podłużnych. Jednak dla porządku, przynajmniej na początkowym etapie nauki stosowania rachunku całkowego warto udowodnić rachunkowo, że rzeczywiście wszystkie składowe poprzeczne się znoszą.

Aby przeprowadzić takie rachunki, spójrzmy najpierw na rysunek nr 2.

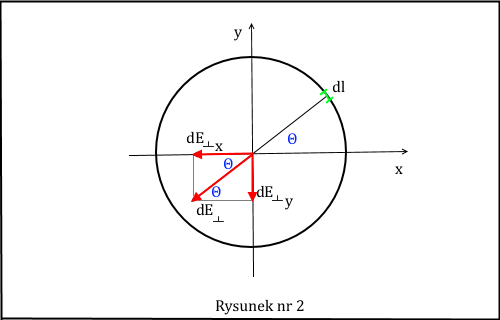
Widzimy na nim poprzeczną składową pola elektrycznego pochodzącą od wybranego elementu różniczkowego dl naszego pierścieniowego przewodnika zrzutowaną równolegle na płaszczyznę osi xy z rysunku nr 1. Kąt Θ liczy się jako dodatni od osi x w kierunku przeciwnym do ruchu wskazówek zegara. Ta składowa pola elektrycznego rozkłada się z kolei na składową wzdłuż osi x równą

dE_⊥x = dE_⊥·cosΘ , (6)

oraz składową wzdłuż osi y równą

dE_⊥y = dE_⊥·sinΘ . (7)

Aby móc przeprowadzać rachunki musimy jeszcze policzyć, ile jest równa sama składowa poprzeczna dE_⊥. Zgodnie z rysunkiem nr 1 jest ona równa

dE_⊥ = dE·cosα . (8)

czyli uwzględniając dane zadania ( cosα = R/[R² + d²]^1/2 ) oraz wzór (5)

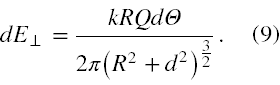
Aby wyliczyć ile jest równe E_⊥x, czyli suma wszystkich dE_⊥x (6) musimy je posumować po wszystkich możliwych kątach Θ, jakie odpowiadają naszemu pierścieniowemu przewodnikowi. Nie ulega wątpliwości, że należy wykonać całkę

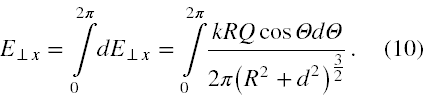
Ponieważ od kąta Θ zależy tylko cosΘ, więc faktycznie pozostaje do wykonania wyłącznie następująca całka, która jest równa 0

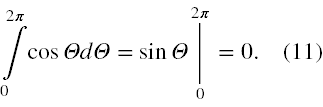
Pozostałe elementy wzoru (10), to stałe w całkowaniu, więc E_⊥x = 0. Sumowanie składowych dE_⊥y analogicznie sprowadzi się do wykonania całki z funkcji sinΘ, która w przedziale od 0 do 2π również jest równa 0. Tak więc udowodniliśmy, że istotnie źródłem pola elektrycznego w punkcie A są tylko składowe podłużne.

Składowa podłużna dE_∥ pola elektrycznego w punkcie A, zgodnie z rysunkiem nr 1 jest równa

dE_∥ = dE·sinα, (12)

a uwzględniając dane zadania ( sinα = d/[R² + d²]^1/2 ) wynosi ostatecznie (we wzorze (13) tylko drugie ″d ″ oznacza różniczkę!)

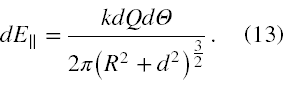
Aby policzyć całkowite pole w punkcie A należy zatem wysumować składowe podłużne pola elektrycznego dla wszystkich możliwych kątów naszego pierścieniowego przewodnika (13). Skoro te kąty zawierają się ponownie w przedziale od 0 do 2π, więc musimy policzyć następującą całkę

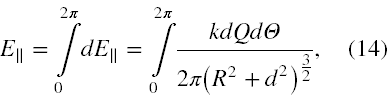
która jest jeszcze prostrza, bo wynosząc stałe przed znak całki musimy tylko wyliczyć całkę z dΘ, która we wskazanym wyżej przedziale jest równa po prostu 2π. Tak więc otrzymujemy wynik, że pole elektryczne w punkcie umieszczonym zgodnie z warunkami zadania jest równe