Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 1

Szczegóły

Kategoria: Publikacje naukowe

Opublikowano: piątek, 10 sierpień 2018 18:25

Autor : Janusz Szcząchor

Do we know everything about bound stationary states?

Abstract: The Bohr model and the Schrödinger equation are compared with each other. The reason for interest in deriving its stationary equation is indicated.

1. Model Bohra, a równanie Schrödingera dla przypadku atomu wodoropodobnego

Zaczniemy nasze rozważania od przypomnienia wybranych faktów dotyczących modelu Bohra (¹). Jako, że elektron w tym modelu posiada tor ruchu, to jest on faktycznie modelem klasycznym. Jedynie nieklasycznym jest sposób, w jaki wybieramy dozwolone ruchy elektronów spośród wszystkich klasycznie dostępnych. Te wybrane ruchy będziemy traktować jako klasyczne związane stany stacjonarne (²).

Model Bohra w części nas interesującej zasadza się na następujących faktach [2].

1. Elektron w atomie wodoropodobnym porusza się tylko po dozwolonych orbitach kołowych, tj. takich dla których moment pędu ma wartość zgodną z poniższą zależnością

   m_er_nv_n = nħ , (1)

   a indeks n (³) numeruje kolejne dozwolone orbity, przy czym dopuszczalne jego wartości to kolejne liczby naturalne, czyli 1, 2, 3, ... .

2. Siła Coulomba z jaką jądro przyciąga elektron jest siłą dośrodkową zmuszającą go do ruchu po okręgu wokół tegoż jądra.

3. Całkowita energia atomu w n-tym stanie kwantowym jest dana jako

   

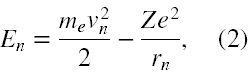
   gdzie Z, to liczba atomowa atomu wodoropodobnego.

4. Uwzględniając warunek 'kwantowy' (1) możemy energię atomu wodoropodobnego w klasycznym związanym stanie stacjonarnym wyrazić jako

   

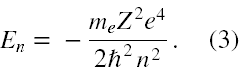
   Jeżeli we wzorze tym zastąpimy masę elektronu m_e masą zredukowaną elektronu µ uwzględniającą ruch elektronu wokół ruchomego jądra, to otrzymamy dobrą zgodność w wynikami doświadczalnymi.

Co na to mechanika kwantowa?

Jeśli chodzi o równanie Schrödingera dla atomu wodoropodobnego, to podaje ono dokładnie ten sam wzór (3) na wartość energii dozwolonych związanych stanów stacjonarnych [3].

Jest jednak istotne ale. W modelu Bohra wartości energii i momentu pędu były kwantowane (numerowane) tą samą liczbą kwantową n. W równaniu Schrödingera już tak nie jest. Moment pędu ma teraz własną liczbę kwantową l, a jego dozwolone wartości to

gdzie l może oprócz liczby naturalnej być także 0.

Z kolei główna liczba kwantowa n jest już teraz funkcją innych liczb kwantowych zgodnie z poniższym wzorem

gdzie n', to radialna liczba kwantowa, która również może być tylko liczbą naturalną lub 0.

Porównajmy ze sobą opis stanu podstawowego atomu wodoropodobnego według obu formalizmów.

W modelu Bohra taki atom w stanie podstawowym jest opisany główną liczbą kwantową n = 1, czyli jego moment pędu jest równy ħ. Ponieważ promień orbity jest niezerowy, zatem pęd elektronu w tym stanie jest również niezerowy.

W modelu Schrödingera dla n = 1, zarówno n', jak i l są równe 0, zatem moment pędu elektronu w tej sytuacji musi być równy 0. Klasycznie jest to tylko wtedy możliwe, gdy elektron porusza się ruchem wahadłowym, tam i z powrotem wzdłuż jednej ze średnic orbity kołowej przez środek jądra atomowego.

Podsumowując widzimy, że formalizm kwantowy prowadzi do poważnych problemów interpretacyjnych co do tego na czym polega ruch elektronu w związanych stanach stacjonarnych. Aby bliżej przyjrzeć się temu problemowi warto byłoby się najpierw dowiedzieć się jak Schrödinger wyprowadził swoje równanie, a zwłaszcza jakie w tym celu przyjął założenia.

2. Niektóre okoliczności powstania mechaniki kwantowej

Jakiś czas temu znalazłem w internecie następujący dialog. Uczeń szkoły średniej pyta pracownika naukowego uniwersytetu, “Jak się wyprowadza równanie Schrödingera?” Profesor odpowiada, “Równania Schrödingera nie można wyprowadzić, można je tylko zapostulować.”

Gdy zajrzymy do podstawowych podręczników mechaniki kwantowej wykorzystywanych na uczelniach od kilkudziesięciu lat, to rzeczywiście możnaby dojść do takiego wniosku. Jeśli jednak zajrzymy do oryginalnych prac Schrödingera [4],[5],[6],[7], to przynajmniej my nie możemy się z tym zgodzić.

Dla porządku tylko przypomnę, że pojęcie funkcji falowej do fizyki wprowadził w roku 1924 Louis de Broglie. A jak się to stało oddajmy głos Maxowi Bornowi [8].

"Kilka lat wcześniej ten drugi przyjął odważne założenie, wsparte przez znakomite rozważania teoretyczne, że dualizm falowo-korpuskularny znany fizykom w przypadku światła musi także być słuszny dla elektronów. Do każdego elektronu poruszającego się swobodnie przynależy fala płaska o skończonej długości fali, której wartość jest wyznaczona poprzez stałą Plancka i masę."

Zgodnie z powyższym, jako wzór na długość tej fali Louis de Broglie przyjął wzór znany z teorii fotonów Planck'a-Einsteina

λ = h/p. (6)

Hipoteza ta została doświadczalnie potwierdzona przez Davissona samodzielnie, potem z Germerem, także przez G.P. Thomsona, Tartakowskiego, Szczeniowskiego, Sterna i Estermana, i wielu innych.

O ile zatem potrafiono podać długość funkcji falowej swobodnej cząstki materialnej, to przypadek elektronu związanego, na przykład w atomie wodoru, pozostawał zagadką. Zagadnienie to rozwiązał Schrödinger wskazując, że do podania postaci funkcjonalnej funkcji falowej jest potrzebne specjalne równanie, później nazwane jego nazwiskiem. Równanie to jest słuszne w każdym nierelatywistycznym przypadku, a Louis de Broglie tak naprawdę to miał wielkie szczęście, że po prostu odgadł postać tej funkcji dla przypadku swobodnego elektronu.

Schrödinger w swoich pracach zawarł dwa wyprowadzenia swojego równania. Pierwsze w [4], dla przypadku niestacjonarnego, o kórym później napisał w stopce w [5].

"Ta metoda postępowania nie będzie już rozwijana dalej w tej pracy. Naszym celem było tylko podać tymczasowy, szybki przegląd zewnętrznego związku między równaniem falowym i równaniem Hamiltona-Jacobiego (⁴)".

Oraz drugie, dla przypadku niestacjonarnego zawarte w [5], rozwinięte dalej w [7].

Celem wyjaśnienia dlaczego szczególnie, naszym zdaniem, dla interpretacji funckji falowej jest istotne pierwsze wyprowadzenie równania Schrödingera odbiegnijmy trochę od tematu i przypomnijmy, że jednym z postulatów mechaniki kwantowej jest założenie o liniowości równań kwantowych. Co to oznacza zacytujmy tu [3].

"Zakładamy, że wszystkie funkcje własne dowolnej zmiennej dynamicznej tworzą zupełny układ funkcji w tym sensie, że każda funkcja ciągła może być przedstawiona w postaci ich kombinacji. Jest to założenie matematyczne, a nie fizyczne ... ."

Mając to na względzie zwróćmy uwagę na to, co najbardziej jest interesujące w fizyce atomowej, czyli przejścia kwantowe. Weźmy je na przykładzie atomu wodoru. Schrödinger oprócz rozwiązania swojego równania dla wodoru opracował też stacjonarny rachunek zaburzeń, ale jak opisać przy pomocy formalizmu mechaniki kwantowej problem przejść kwantowych pokazał dopiero Dirac.

Zgodnie z jego teorią [11] przyjmujemy, że atom wodoru jest systemem niezaburzonym i jest opisany hamiltonianem H₀, którego układ stanów własnych znamy. Niech operatorem zaburzającym, czyli wywołującym przejścia kwantowe w atomie wodoru będzie operator V. Zatem atom wodoru wraz z zaburzeniem jest opisany niestacjonarnym równaniem Schrödingera w formie

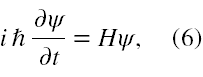
gdzie H = H₀ + V.

Procedura rozwiązywania równania (6) polega na rozwinięciu zawartej w nim funkcji falowej ψ na funkcje własne u_ne^-iE_nt/ħ niezaburzonego równania falowego z czasem, czyli

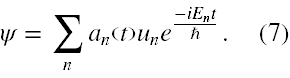
Jak założył Dirac współczynniki a_n(t) są tylko funkcjami czasu i |a_n(t)|² jest prawdopodobieństwem tego, że atom wodoru w chwili t jest w stanie u_ne^-iE_nt/ħ.

Spójrzmy teraz na powyższą procedurę z punktu widzenia statystycznej interpretacji funkcji falowej. W tym miejscu interpretację statystyczną będziemy rozumieli w sposób uproszczony, ograniczając się tylko do badania własności gęstości prawdopodobieństwa położenia. Dowolne rozwiązanie niestacjonarnego równania Schrödingera dla niezaburzonego atomu wodoru ma tę własność, że

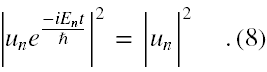
Zatem tutaj równanie niestacjonarne nie może wnieść czegokolwiek nowego do interpretacji statystycznej wodorowej funkcji falowej.

Z kolei funkcja dana równaniem (7) z uwagi na swoją budowę, która również nie wnosi żadnej nowej funkcjonalności zależnej od zmiennych położeniowych w stosunku do u_n, tak samo nie jest w stanie wnieść czegoś nowego do interpretacji statystycznej wektorów stanu. Tak więc naszym zdaniem zasadny jest wniosek, że istota tej interpretacji powinna leżeć w wyprowadzeniu stacjonarnego równania Schrödingera. To właśnie wyprowadzenie tego równania powinno rzucić zasadnicze światło na interpretację statystyczną funkcji falowej.

Na podkreślenie zasługuje fakt, że Schrödinger w pracach [5],[6],[7] zasadniczo już nie analizował na tle interpretacyjnym związku między torem ruchu cząstki, a jego funkcją falową, natomiast skupił się na znalezieniu ewolucji czasowej tej funkcji, szczególnie analizując przypadek odgadniętej przez de Broglie swobodnej funkcji falowej. Stąd w części 2 niniejszego artykułu przejdziemy do analizy wyprowadzenia stacjonarnego równania Schrödingera zawartego w [4].

UWAGI

(¹) Może kogoś zastanawiać dlaczego tu przypominamy model Bohra, który przecież 'ma niewiele wspólnego z rzeczywistym światem'. Nie zamierzamy tu bronić naukowo tego modelu. Jednak ma on wielkie zalety jako model czytelny poglądowo do tego stopnia, że w programach, czy prezentacjach o charakterze popularnonaukowym, nawet jeśli mówi się o konsekwencjach mechaniki kwantowej (a nie modelu Bohra) dla fizyki atomowej, to i tak ilustruje się je na ogół animacjami zgodnymi z modelem Bohra, a nie mechaniką kwantową.

(²) Formalne wyjaśnienie w ramach mechaniki kwantowej, jaki stan kwantowy jest stacjonarnym, a do tego związanym można znaleźć na przykład w [1].

(³) W pierwszej części tego artykułu pogrubienia liter w żadnym wypadku nie są oznaczeniem wektora, zostały tu zastosowane jedynie celem zwiększenia czytelności tekstu.

(⁴) Schrödinger nie wyjaśnił, co było powodem braku dalszego jego zainteresowania pierwszą metodą, zapewne była to niemożność wyprowadzenia tą drogą prawidłowej postaci równania niestacjonarnego. Na zasadność takiego wniosku może wskazywać fakt, że w pracy [9] mającej chyba na celu przybliżenie jego teorii angielskojęzycznym czytelnikom Schrödinger nic nie wspomina o pierwszej metodzie wyprowadzenia swojego równania. Tłumaczenie prac [4],[5],[6],[7] na angielski ukazało się dopiero dwa lata później w [10]. Jednak chyba Schrödinger sam nie docenił swojej pierwszej metody, albowiem naszym zdaniem jest ona kapitalnym źródłem interpretacji funkcji falowej. Po drugie, w przedstawionej w [7] jego własnej,oryginalnej interpretacji funkcji falowej można, wbrew słowom Schrödingera, dostrzec wielki wpływ tego pierwszego wyprowadzenia.

LITERATURA

[1] L.D. Landau, E.M. Lifshitz, Quantum Mechanics, Non-relativistic Theory, §10, Pergamon, Oxford, 1958.

[2] Sz. Szczeniowski, Fizyka Doświadczalna, Część V, Fizyka Atomu, §21, PWN, Warszawa, 1974.

[3] L. Schiff, Quantum Mechanics, §16, McGraw-Hill, New York, 1968.

[4] E. Schrödinger, Quantisierung als Eigenwertproblem I, Annalen der Physik, 79, 361 (1926).

[5] E. Schrödinger, Quantisierung als Eigenwertproblem II, Annalen der Physik, 79, 489 (1926).

[6] E. Schrödinger, Quantisierung als Eigenwertproblem III, Annalen der Physik, 80, 437 (1926).

[7] E. Schrödinger, Quantisierung als Eigenwertproblem IV, Annalen der Physik, 81, 109 (1926).

[8] M. Born, The statistical interpretation of quantum mechanics, Nobel Lecture (1954).

[9] E. Schrödinger, An Undulatory Theory of the Mechanics of Atoms and Molecules, Physical Review, 28, 1049 (1926).

[10] tłum. J. F. Schearer, W. M. Deans, Collected Papers on Wave Mechanics, Blackie and Son, London, 1928.

[11] P. A. M. Dirac, Proc. Roy. Soc. (London) A114, 243 (1927).