Metody rozwiązywania równania Diraca - część 1

Szczegóły

Kategoria: Równanie Diraca

Opublikowano: czwartek, 26, marzec 2015 20:36

Autor : Janusz Szcząchor

Problem nr 1, Janusz Szcząchor

Znajdź rozwiązania równania Diraca w zewnętrznym potencjale elektrostatycznym o stałej wartości, typu bariery schodkowej. Rozwiązania powinny być funkcjami własnymi operatora energii, jak i operatora pędu. Użyj przedstawienia standardowego oraz spinorowego macierzy Diraca. Przedtem wyprowadź ogólną metodę rozwiązywania równania Diraca w zewnętrznym potencjale składającym się z potencjału skalarnego.

Rozwiązanie

§1 Co to jest równanie Diraca?

Zapewne już z kursu fizyki w szkole średniej wiesz, że dzielimy fizykę na relatywistyczną i nierelatywistyczną. Podobnie jest z mechaniką kwantową.

Historycznie mechanika kwantowa zaczęła się od wprowadzenia przez Louisa de Broglie'a pojęcia funkcji falowej (wcześniej raczej mówi się o fizyce kwantowej). Jednak dopiero wprowadzenie przez Erwina Schrödingera jego nierelatywistycznego równania pozwalającego opisać zachowanie elektronów w polu elektromagnetycznym było punktem zwrotnym w jej rozwoju.

Próby wyprowadzenia równania, które byłoby relatywistycznym partnerem równania Schrödingera podjęło kilku fizyków - Klein, Gordon, Fock. Lecz pierwszym był chyba jednak znowu Schrödinger, który od razu zauważył, że daje ono niewłaściwe poziomy energetyczne dla atomu wodoru i dlatego nim się nie interesował. Dopiero w miarę upływu czasu stało się jasne, że opisuje ono cząstki o spinie 0, a więc nie elektrony.

Stąd wielką zasługą Diraca było to, że usilnie dążył do znalezienia równania poprawnie opisującego elektrony. Chociaż jak dziwi się Steven Weinberg [1] Diracowi przeszkadzał brak dodatniej określoności gęstości prawdopodobieństwa w równaniu Kleina-Gordona, a nie to, że nie opisuje ono cząstek o spinie ½. Historię odkrycia równania Diraca możesz znaleźć w książce Weinberga oraz w wielu innych podręcznikach mechaniki kwantowej.

Równanie Diraca da się zapisać jako

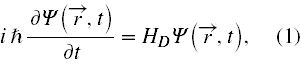
gdzie celowo oznaczyłem hamiltonian indeksem D. Dirakowski operator Hamiltona dla ładunku elektrycznego poruszającego się w potencjale elektromagnetycznym A^µ = (A₀,A) można zapisać w formie

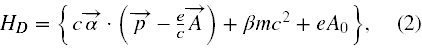
gdzie stosuję oznaczenia wzorowane na podręczniku Bjorkena i Drella [2]. Ponadto przyjmujemy, że tensor metryczny g_µν = (1,-1,-1,-1), zatem A₀ = A⁰, jak i x₀ = x⁰. Na szczególną uwagę tutaj zasługuje ładunek e. Jest on wzięty wraz ze swoim znakiem. Tzn. dla elektronu jest on równy -|e|, a dla pozytonu +|e|. Ponadto przez p należy rozumieć wektorowy operator pędu,tj.

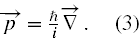
Rozwiązaniem równania jest bispinor Ψ(r,t),który jest 4-wektorem, na ogół zespolonym. Stąd α i β są macierzami 4×4.

§2 Ogólny punkt widzenia na rozwiązywanie równania Diraca

Wyłożone w podręcznikach metody rozwiązywania tego równania sprawiają wrażenie chaotycznych. Dlatego najpierw trzeba po prostu zauważyć, że równanie Diraca, to układ 4 równań różniczkowych cząstkowych pierwszego rzędu. Aby taki układ rozwiązać trzeba go rozprzęgnąć.

Gdy położymy A^μ = 0, to otrzymujemy równanie swobodne. Jego stacjonarne rozwiązanie jest podane w wielu podręcznikach. Można wtedy równanie Diraca sprowadzić do układu równań algebraicznych, patrz np. [3]. Choć to możliwe w naszym problemie, to nie pójdziemy tą drogą, bo byłaby bezproduktywna dla dalszych zastosowań.

Kierując się własnym punktem widzenia przypomnijmy, że macierze α i β zostały wyznaczone z żądania, aby były hermitowskie, antykomutowały ze sobą i ich kwadrat był macierzą jednostkową (tzn. aby kwadrat hamiltonianu Diraca przechodził w hamiltonian Kleina-Gordona, czyli prowadził do prawidłowej relatywistycznej zależności między pędem i energią). Warunki te jednak nie pozwalają na ustalenie jednoznacznej postaci tych macierzy.

Istnieje wiele przedstawień macierzy α i β, o których się twierdzi, że są fizycznie równoważne, bo spełniają te same żądania. Jeśli chodzi o żądania dla równań swobodnych to prawda, ale tu muszę zwrócić uwagę, że gdy wstawimy pole, to się okazuje, że kwadrat hamiltonianu Diraca (z polem) nie jest już równy hamiltonianowi Kleina-Gordona (z polem). Dochodzą dwa człony sprzęgające pola E i H ze spinem [4] .

Z kolei zwróćmy uwagę, że rozwiązania Ψ(r,t) muszą mieć określoną strukturę, aby poprawnie opisywać istnienie cząstek i antycząstek oraz fakt, że obie te cząstki mogą mieć dwa możliwe kierunki rzutu spinu na wybraną oś. Mając to na względzie rozwiązania swobodne uczą dalej, że powinniśmy podzielić czteroskładnikowy bispinor na dwa dwuskładnikowe spinory. A zatem interesujące są te przedstawienia macierzy Diraca, które dadzą się zapisać jako iloczyny tensorowe macierzy 2×2 (z których te drugie, to macierze Pauliego), bo wtedy jest szansa, że rachunki będą łatwiejsze.

Na niektóre przedstawienia zwrócimy teraz większą uwagę. Np. jeśli chodzi o dowodzenie lorentzowskiej niezmienniczości równania Diraca, to sam odkrywca równania pokazał, że wygodniejsze są macierze γ^μ. Ale co do rozwiązywania równania to szczególne znaczenie mają przedstawienia standardowe i spinorowe. Obydwa mają swoje wady i zalety.

Jeśli chodzi o przedstawienie standardowe, to oprę się na [5] i [6]. Gdy chcemy, aby hamiltonian (2) opisywał elektron w spoczynku, to należy położyć nie tylko A^μ = 0, ale także przyjąć, że operator pędu działając na bispinor Ψ daje 0. Stąd najłatwiej przyjąć, że bispinor Ψ nie zależy od r. Wtedy możemy pozbyć się operatora pędu i równanie Diraca przyjmuje postać

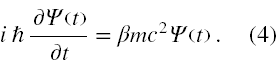
W przedstawieniu standardowym macierz β jest diagonalna, gdzie 1 oznacza 2×2 macierz jednostkową, patrz rysunek nr (5)

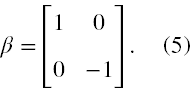
Wtedy równanie (4) rozpada się na cztery niezależne równania, każde na osobną składową, które łatwo scałkować, a rozwiązanie przyjmuje postać

Ψ^r(t) = e^{-iε_rmc2t/ħ} , (5a)

gdzie r = 1,2,3,4, ε_r = +1 dla r = 1 lub 2, oraz ε_r = -1 dla r = 3 lub 4.

Widać stąd po zadziałaniu na Ψ^r(t) operatorem energii, że składowe dla r = 1 lub 2 mają energię +mc², a dla r = 3 lub 4 składowe -mc², czyli opisują "antycząstki" (użyłem cudzysłowu celowo).

W ten sposób rozwiązanie równania (4) rozpadło się na cztery niezależne liniowo rozwiązania. Oznacza to, że rozwiązania swobodne dla dowolnej wartości pędu, gdy ten zmierza do 0 muszą przejść w któreś z powyższych rozwiązań.

Jednak jak zaobserwowałem przedstawienie standardowe ma istotną wadę. A mianowicie, gdy wstawimy zewnętrzne pola, to często aby rozprzęgnąć układ równań (1)-(2) trzeba doprowadzić jedno z równań do równania różniczkowego czwartego rzędu, aby pozostałe rozwiązania uzyskać tylko drogą różniczkowania. Jest to ze wszechmiar niewygodne. Tymczasem przedstawienie spinorowe umożliwia to już na poziomie równania drugiego rzędu. Dlatego jest tak interesujące!

Jednak to przedstawienie nie daje tak prostego posegregowania rozwiązań, bo macierz β ma obecnie taką postać

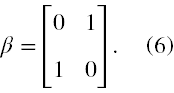
Tutaj ponownie 1 oznacza 2×2 macierz jednostkową. Teraz górne i dolne składowe bispinora Ψ(t) są ze sobą mieszane. Wprowadźmy zatem w (4) podział na górne i dolne składowe bispinora oraz wstawmy tam (6).

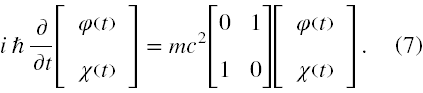
Otrzymaliśmy w ten sposób układ dwóch równań różniczkowych 1-rzędu.

Rozwiążemy go różniczkując stronami po czasie pierwsze równanie oraz też stronami mnożąc je przez iħ i mamy

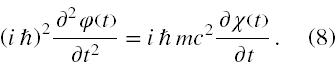
Następnie za pochodną χ(t) wstawimy wyrażenie z drugiego równania (7) i otrzymujemy równanie II rzędu tylko na φ,

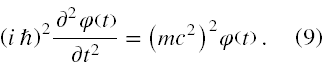
Porządkując (9) otrzymujemy w końcu

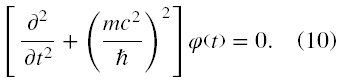
Niech φ = e^kt i mamy po wstawieniu do (10)

k²+m²c⁴/ħ² = 0,

czyli

k = ±imc²/ħ.

Jak widać mamy dwa rozwiązania.

I) Niech φ_-(t) = e^(imc2/ħ)t, wtedy z pierwszego równania w (7), po zamianie stron równania, mamy równanie na χ_-(t), z którego wynika, że

χ_-(t) = -e^(imc2/ħ)t.

II) Jeśli χ₊(t) = e^-(imc2/ħ)t to widać, że

χ₊(t) = e^-(imc2/ħ)t.

Działając operatorem energii na jedno lub drugie rozwiązanie widzimy, że rozwiązaniem o dodatniej energii jest

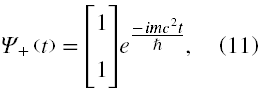
a rozwiązaniem o ujemnej energii jest

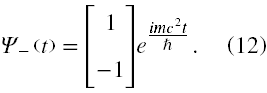
W powyższych wzorach przez 1 oznaczyłem 2-wymiarowe jednokolumnowe wektory takie, że mają one 1 w jednym wierszu, a w drugim 0 (na przemian). Z (7) w sposób oczywisty widać, że φ(t) i χ(t) muszą mieć 1 i 0 jednocześnie na tych samych pozycjach.

Jak pokazałem nie ma tu bezpośredniego przyporządkowania górnych, czy dolnych składowych do znaku energii. Widać też, że równie dobrze moglibyśmy najpierw otrzymać równanie II rzędu na funkcję χ(t) i potem dopiero z równania I rzędu policzyć funkcję φ(t), a obliczane składowe po prostu zamieniłyby się rolami w rozwiązaniu dla ujemnej energii.

§3 Rozwiązanie w przedstawieniu standardowym

Zanim przejdziemy do obliczeń muszę dokonać pewnych wyjaśnień. W podręcznikach zaznaczają się dwie metody rozwiązywania tego problemu. Jedna oparta jest na podstawieniu do swobodnego równania Diraca próbnego rozwiązania w formie fali płaskiej, a następnie znalezieniu żądania, aby zerował się pewien wyznacznik prowadzący do warunku

E _± = ±√(p²c² + m²c⁴),

gdzie E _- jest interpretowane jako energia stanów o ujemnej energii.

Mnie takie postępowanie do końca nie przekonuje. Nie uwzględnia ono faktu, że w rozwiązaniach swobodnych wykładnik eksponentu musi być proporcjonalny do ±p^µx_µ. W żadnym wypadku nie wolno zmieniać względnego znaku między p i E w takim wykładniku bez szczegółowego umotywowania. Aby otrzymać rozwiązania o ujemnej energii trzeba po prostu podstawić drugą funkcję próbną z +p^µx_µ. O tym jaki jest znak wartości własnej energii decyduje jedynie wynik równania własnego (patrz jednak uwagi w §5 [8])

ÊΨ = εΨ,

a nie to co podstawimy za E w wykładniku eksponentu. Sądzę, że pokutuje tu zbyt częste odwoływanie się do relatywistycznego równania Hamiltona-Jacobiego, gdzie z uwagi na brak stosownego operatora energii trzeba po prostu wyciągnąć pierwiastek, aby obliczyć energię. Niestety widać to nawet ze słynnej pracy Diraca [7].

W moim przekonaniu tylko podręcznik Bjorkena i Drella podaje prawidłowe rozumowanie, choć autorzy wprowadzili je bez uciekania się do rozwiązywania układu równań różniczkowych.

Aby otrzymać rozwiązania równania Diraca w stałym potencjale w równaniu (1)-(2) dokonajmy nstp. podstawień:

1. A połóżmy 0,
2. o A₀ będziemy zakładać, że jest stałą,
3. oraz dokonajmy wstępnych przekształceń polegających na podstawieniu jawnej postaci operatora pędu, podzieleniu równania stronami przez iħc i przeniesieniu członów, za wyjątkiem tego zawierającego m, na lewą stronę, a otrzymamy (jako x⁰ rozumiem ct)

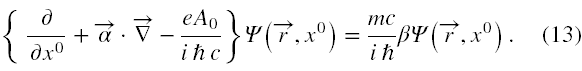
Tak mamy przygotowane równanie Diraca do obliczeń matematycznych. Jeżeli chcemy otrzymać rozwiązania w przedstawieniu standardowym, to w takim przedstawieniu musimy wstawić do (13) macierze α i β. Jeżeli będziemy chcieli uzyskać rozwiązania w innym przedstawieniu, to prostu zmieniamy postacie tychże macierzy.

A zatem podstawiamy

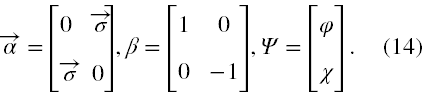
Przenosząc wyrazy z φ na jedną stronę, a z χ na drugą (jeżeli nie będzie to prowadzić do nieporozumień, to nie będziemy teraz jawnie wypisywać zmiennych, od których te funkcje zależą)otrzymujemy następujący układ równań

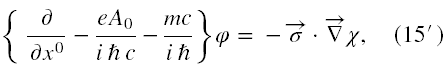
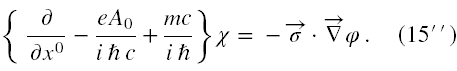
Przypomnijmy (patrz podręczniki polecone w odnośnikach), że istnieje tożsamość

(σ⋅Â)(σ⋅Ê) = Â⋅Ê+iσ⋅[Â×Ê].

Jeżeli za  i Ê do powyższej podstawimy operator nabla, to w wyniku otrzymamy jego kwadrat (tj. sumę trzech drugich pochodnych). Zatem na (15'') podziałajmy stronami operatorem σ⋅∇, który komutuje z ∂/∂x⁰, a A₀ jest tutaj(!) dla niego stałą, dalej za σ⋅∇χ w tym równaniu podstawiamy to co wynika z (15'), w końcu przenosimy wyraz z ∇²φ na lewą stronę ze zmienionym znakiem i otrzymujemy równanie Kleina-Gordona ze stałym potencjałem (16) na φ.

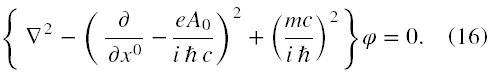
Równania (16) i (15'') tworzą układ, za pomocą którego możemy uzyskać rozwiązanie równania (13) w przedstawieniu standardowym. Po wstawieniu do (16) jako rozwiązanie próbne φ = C ⋅e^{i(pr - Et )/ħ} , gdzie C - pewien stały wektor o postaci

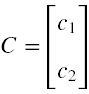
oraz wykonaniu kilku prostych przekształceń otrzymujemy warunek, że

(E - eA₀)² - p²c² - m²c⁴ = 0,

czyli

E = eA₀ ± √(p²c² + m²c⁴).

Z przezorności wprowadzimy oznaczenie κ = ±1, a dozwolone wartości energii przyjmą postać

E₊ = eA₀ + κ⋅√(p²c² + m²c⁴).

Podstawiając do równania (15'') za χ = D⋅e^{i(pr - Et)/ħ} , gdzie D to pewien stały wektor o postaci

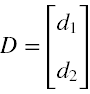
mamy

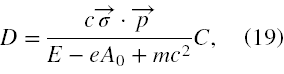
czyli rozwiązaniem o dodatniej energii jest

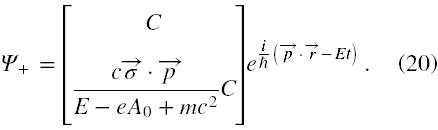
Jeśli podstawimy teraz w równaniu (16) za φ = C ⋅e^{-i(pr - Et )/ħ}, to będzie to rozwiązanie o ujemnej energii. Równanie wiążące E i p przyjmie teraz postać

E_- = - eA₀ + κ⋅√(p²c² + m²c⁴).

Teraz do równania (15'') podstawiamy za χ = D⋅e^{- i(pr - Et)/ħ}, gdzie D to pewien stały wektor o postaci jak poprzednio. Wtedy otrzymamy z (15''), że

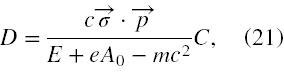
i to χ będzie teraz dużą składową. Możemy stałej C nadać postać

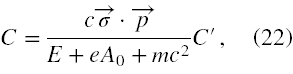
i otrzymamy, że χ będzie równe C'⋅e^{-i(pr - Et)/ħ} . Mamy w ten sposób ładniejszą, bo symetryczną postać rozwiązań. I rozwiązanie o ujemnej energii nabierze postaci

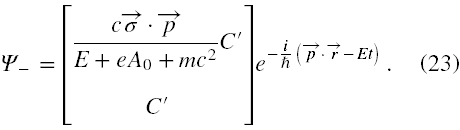
Tutaj C' ma taką strukturę jak C poprzednio. W ten sposób otrzymaliśmy rozwiązania o postaciach jak w podręcznikach. Zmierzając z p → 0 chcemy otrzymać rozwiązania zgodne z otrzymanymi wcześniej dla cząstki spoczywającej.

Analiza wyrażenia cσ⋅p/(E±eA₀+mc²) w powyższym przejściu granicznym z użyciem reguły de L'Hospitala wskazuje, że przy wyborze κ = -1 otrzymamy wyrażenie graniczne postaci mc²/0, czyli nieprawidłowe. Natomiast wybór κ = +1 daje wyrażenie graniczne w formie 0/2mc², czyli poprawne. Zatem teraz dopiero możemy stwierdzić, że musi być κ = +1.

Pozostaje kwestia dotycząca unormowania Ψ†Ψ = 1. Podstawiając w stałych C, jak i C' raz c₁ ( lub c'₁) równe 1, a c₂ ( lub c'₂) równe 0, a potem na odwrót otrzymamy następujące stałe normujące:

a) dla rozwiązań o energii dodatniej

c₁ = c₂ = {(E - eA₀ + mc²)/2(E - eA₀)}^1/2,

b) oraz dla rozwiązań o energii ujemnej

c'₁ = c'₂ = {(E + eA₀ + mc²)/2(E + eA₀)}^1/2.

§4 Rozwiązanie w przedstawieniu spinorowym

Ponownie wyjdziemy od równania Diraca w postaci (13). Teraz podstawiamy macierze α i β w przedstawieniu spinorowym, przy czym bispinor Ψ nadal będziemy przedstawiać jako 4 - składnikowy wektor zawierający w pierwszych dwóch wierszach składowe spinora φ, a w pozostałych dwóch składowe spinora χ. Jeśli nie będzie to prowadzić do nieporozumień, to nie będziemy jawnie wypisywać zmiennych od których one zależą, tj. r i t.

A zatem macierze α i β przyjmują postacie

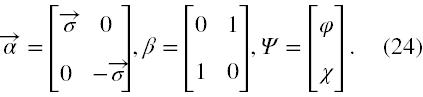
Wtedy równanie (13) rozpada się na następujący układ dwóch równań I rzędu

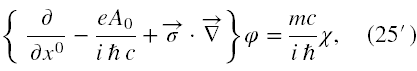
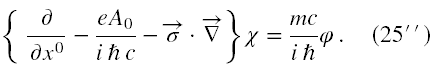
W stosunku do równań (15') i (15'') widać istotną różnicę, bo teraz oba operatory różniczkowe działają tylko na jedną składową, druga jest wymnożona przez stałą.

Mnożymy równanie (25'') stronami przez mc/iħ i za (mc/iħ)χ podstawiamy to co wynika z (25'). A₀ jest ponownie stałą dla różniczkowania po zmiennych czasowej i przestrzennych. Po przeniesieniu z przeciwnym znakiem (mc/iħ)² z prawej na lewą stronę oraz pomnożeniu całego równania przez (-1) ponownie otrzymujemy równanie (16). W tym momencie nie ma jeszcze różnicy między przedstawieniem standardowym i spinorowym.

Za rozwiązanie próbne do (16) podstawiamy φ = C ⋅ e^{i(pr - Et )/ħ}, które przynależy do dodatniej wartości własnej energii układu i w wyniku tego równania II rzędu ponownie otrzymujemy wzór Einsteina wiążący E i p w formie

E₊ = eA₀ + κ⋅√(p²c² + m²c⁴).

W postulowanym rozwiązaniu, podobnie jak i dla przedstawienia standardowego stała C, to dwuskładnikowy wektor zawierający na pierwszej pozycji stałą c₁, a na drugiej stałą c₂.

Taką funkcję φ wstawiamy do równania (25') i z niego wprost otrzymujemy, że (teraz nie musimy o χ nic zakładać)

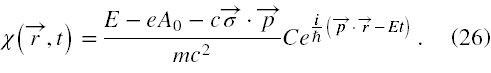
Ponieważ podręczniki akademickie na ogół w ogóle nie podają rozwiązań równania Diraca w przedstawieniu spinorowym, podam jawnie tu te rozwiązania.

Po pierwsze przypomnimy, że macierze Pauliego mają formę

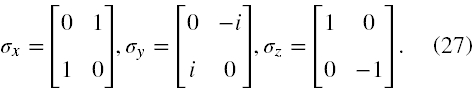
Wtedy macierz stojąca w (26) przed stałą C po rozpisaniu na składowe ma postać

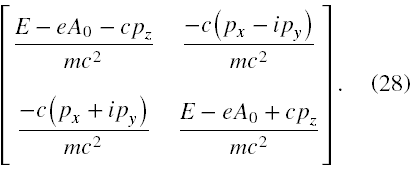
A zatem rozwiązania o dodatniej energii przy oznaczeniu, że stały wektor C ma poniższą formę

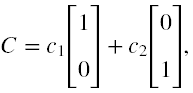
przyjmują postać

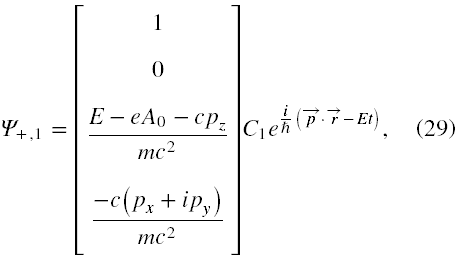
oraz

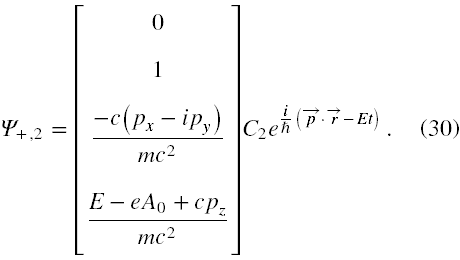
Jak widać, gdy p → 0, to (E - eA₀) → κmc². A zatem w granicy cząstki spoczywającej rozwiązania Ψ_+ , 1 i Ψ_+ , 2 będą zawierały w kolumnie wartości 0 i 1 pod warunkiem, że wybierzemy tylko κ = +1.

Aby otrzymać rozwiązania o ujemnej wartości energii podstawiamy do (16) za rozwiązanie próbne ψ = C ⋅ e ^{- i(pr - Et )/ħ} i otrzymujemy relację Einsteina wiążącą E i p w formie

E_- = - eA₀ + κ⋅√(p²c² + m²c⁴).

Z kolei wstawiając powyższe ψ do równania (25') otrzymujemy, że

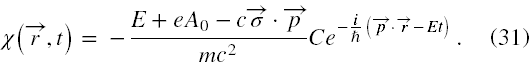
Tym samym rozwiązania Ψ_- , 1 i Ψ_- , 2 o ujemnej energii będą miały postać taką jak (29) i (30) z tym, że w 3 i 4 wierszu kolumny będą występowały wyrażenia o znaku przeciwnym, przy polu eA₀ będzie znak '+' (a nie '-'), a w wykładniku eksponenta będzie też przeciwny znak.

Jeśli chodzi o przejście do granicy cząstki spoczywającej, to istotna jest analiza wyrażenia -(E+eA₀∓cp_z)/mc² = -[κ√(p²c² + m²c⁴)∓cp_z]/mc². Gdy będziemy zmierzać z p → 0, to otrzymamy rzeczywiście odpowiednio dla Ψ_- , 1 w trzecim wierszu -1, a dla Ψ_- , 2 w czwartym wierszu też -1, ale pod warunkiem, że przyjmiemy wyłącznie κ = +1.

Unormowanie Ψ†Ψ = 1 jest o tyle teraz niewygodne, że w rozwiązaniach Ψ_+ , 1 i Ψ_- , 1 w trzecim wierszu mamy (E ±eA₀) - cp_z, a w rozwiązaniach Ψ_+ , 2 i Ψ_- , 2 w czwartym wierszu jest (E ±eA₀) + cp_z. W wyniku tego otrzymamy dwie różne stałe normujące, które będą równe ( 1 → "-", 2 → "+") jeśli chodzi o znaki przy cp_z, a przy eA₀ będzie znak '-' dla rozwiązań o dodatniej enenrgii, a '+' dla rozwiązań o ujemnej energii

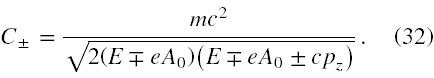
§5 Uwagi końcowe [8]

Na zakończenie należy zwrócić uwagę, że uniwersyteckie kursy mechaniki kwantowej skupiają się na stanach związanych (sam tego doświadczyłem), tak że można z przyzwyczajenia zapomnieć o tym, że w teorii kwantowej też rozróżnia się pęd uogólniony i pęd mechaniczny (inaczej kinetyczny).

Jeżeli w polu elektromagnetycznym, tak jak w rozpatrywanych przypadkach, mamy cząstki swobodne, tj. nie mamy stanów związanych, to ich energia i pęd są dane nie poprzez pędy uogólnione, a przez pędy cząstek.

W naszym przypadku oznacza to, że operator energii cząstki Diraca w polu zewnetrznym jest dany jako

Ê = iħ∂/∂t - eA₀.

Więcej na ten temat patrz np. [9]. Jest to jednak podręcznik poświęcony mechanice klasycznej. Ja niestety dotychczas nie spotkałem książki przeprowadzającej dyskusję tego zagadnienia od strony kwantowej.

Literatura

[1] Steven Weinberg, Teoria Pól Kwantowych,Tom I "Podstawy", PWN, W-wa 1999,strona 33.

[2] J.D.Bjorken,S.D.Drell, Relatywistyczna teoria kwantów,Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985.

[3] A.S.Dawydow,Mechanika kwantowa, PWN, W-wa 1969, §61.

[4] W.B.Bierestecki, E.M.Lifszyc, L.P.Pitajewski,Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §32.

[5] J.D.Bjorken,S.D.Drell, Relatywistyczna teoria kwantów,Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985. §1.4

[6] W.B.Bierestecki, E.M.Lifszyc, L.P.Pitajewski,Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §21 i §23.

[7] P.A.M. Dirac, Proc.R.Soc. A126, 360(1930) - strony 360-361.

[9] W.Rubinowicz,W.Królikowski, Mechanika Teoretyczna, Roździał 2, §12 Równania Lagrange'a drugiego rodzaju. Pędy uogólnione., Roździał 3, §1 Równania kanoniczne Hamiltona, § 3 Równanie Hamiltona-Jacobiego, PWN, Warszawa 1978.