W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 17
- Szczegóły
- Kategoria: Zadania z fizyki
- Opublikowano: środa, 16, listopad 2015 21:55
- Autor : Janusz Szcząchor
- O mnie:
- Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu
zadanie nr 2.75, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki",WSiP,Warszawa 1976
Przez blok nieruchomy A (rys. 2.27) przełożona jest nić, na której jednym końcu wisi ciężarek o masie m1 = 3 kg, a na drugim końcu blok ruchomy B. Przez blok B przerzucona jest nić z zawieszonymi na jej końcach ciężarkami m2 = 1 kg i m3 = 2 kg. Z jakim przyspieszeniem będzie się poruszać ciężarek m1? Masy bloków i nici są do zaniedbania.
Rozwiązanie
Analizę zadania zacznijmy od zastanowienia się, co się będzie działo w układzie, w którym ciężarek m1 jest unieruchomiony? Wtedy ruch ciężarków m2 i m3 będzie wynikał tylko z działania sił ciężkości tych mas, patrz rysunek nr 1.
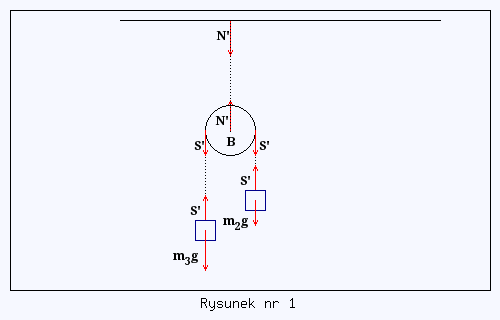
Blok B jest kołem, a więc ma równe ramiona i siły S' są identyczne. Skoro na razie dolny blok się nie porusza, więc siły te są zrównoważone siłą N' (pogrubienie oznacza wektory), zgodnie z poniższym równaniem
S' + S' + N' = 0 . (1)
Skoro masa m3 jest większa od m2, więc m3 będzie się poruszać w dół, a m2 w górę. Z uwagi na nierozciągliwość nici przyspieszenia obu ciał będą identyczne co do wartości, a zwroty ich będą przeciwne. Równania wyrażające II zasadę dynamiki dla tych ciężarków to
m3g - S' = m3ax , (2)
S' - m2g = m2ax . (3)
Ponieważ mamy układ dwóch równań na dwie niewiadome, S' i ax, więc możnaby ten układ rozwiązać.
Zastanówmy się teraz, co się stanie, gdy ciężarek m1 może się poruszać (zwróć uwagę, że m1 = m2 + m3)? Załóżmy, że będzie się poruszał w dół. Wtedy cały dolny układ ciężarków powinien poruszać się w górę, patrz rysunek nr 2.
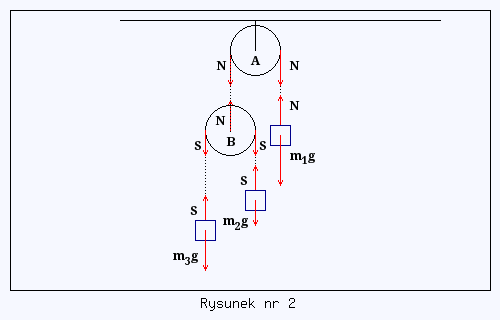
Zatem siła N, aby zmusić układ dolny do ruchu w górę musi być większa od N'. Tym samym siły S powinny być większe od S'. Mamy zatem
S + S + N = 0 . (4)
Stąd II zasada dynamiki Newtona dla m1 wygląda następująco
m1g - N = m1a . (5)
Z uwagi na ruch dolnego układu w górę na ciężarki m2 i m3 powinny działać dodatkowe siły ΔS = S - S', dzięki którym oba ciężarki powinny uzyskać dodatkowe przyspieszenie w górę. Będzie się ono albo dodawać, albo odejmować z przyspieszeniem ciężarków, wynikającym z równań (2) i (3) w zależności od zwrotu ich ruchu. Zatem teraz II zasada dynamiki Newtona dla dolnych ciężarków przyjmuje postać
S - m3g = (a - ax)m3 , (6)
S - m2g = (a + ax)m2 . (7)
Mamy teraz cztery równania na cztery niewiadome, a więc układ powinien dać się rozwiązać.
Opuszczając w (4) notację wektorową otrzymujemy, że
S + S = N . (8)
Dodając stronami (6) i (7) oraz wykorzystując (8) otrzymujemy nowe równanie
N - (m2 + m3)g = (a - ax)m3 + (a + ax)m2
= a(m2 + m3) + ax(m2 - m3) . (9)
Wykorzystując (5) możemy pozbyć się N w (9) i otrzymujemy
m1g - m1a - (m2 + m3)g = a(m2 + m3) + ax(m2 - m3) . (10)
Wyraz z a przenosimy na drugą stronę ze zmienionym znakiem, po lewej stronie wyłączamy g przed nawias klamrowy i w końcu dostajemy
{m1 - (m2 + m3)}g = a(m1 + m2 + m3) + ax(m2 - m3) . (10a)
Z kolei odejmując stronami (6) od (7) otrzymujemy, że
(m3 - m2)g = (m2 - m3)a + (m2 + m3)ax . (11)
W końcu obliczamy ax
ax = g(m3 - m2)/(m2 + m3) - a(m2 - m3)/(m2 + m3) . (12)
Równanie (10a) dzielimy stronami przez (m2 - m3) oraz za ax wstawiamy to co wynika z (12), następnie dwa wyrazy z g grupujemy po jednej stronie, a drugie dwa z a po przeciwnej, tam gdzie trzeba zmieniając znak ułamka na przeciwny, wyłączamy g oraz a przed nawiasy klamrowe i mamy kolejne równanie
g { [m1 - (m2 + m3)]/(m2 - m3) - (m3 - m2)/(m2 + m3) } =
a { (m1 + m2 + m3)/(m2 - m3) - (m2 - m3)/(m2 + m3) } . (13)
Mnożymy stronami (13) przez (m2 - m3)(m2 + m3), skracamy odpowiednie mianowniki, wymnażamy nawiasy oraz redukujemy wyrazy podobne powstałe z tego mnożenia, w końcu możemy obliczyć, że
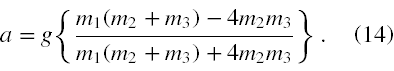
Podstawiając za masy odpowiednie dane widzimy, że ciężarek o masie m1 rzeczywiście porusza się w dół z przyspieszeniem a = g/17.
