Czy wszystko już wiemy o związanych stanach stacjonarnych? - Część 2

Szczegóły

Kategoria: Publikacje naukowe

Opublikowano: piątek, 10 sierpień 2018 18:25

Autor : Janusz Szcząchor

Do we know everything about bound stationary states?

Abstract: The first method of deriving the Schrödinger equation is analyzed. The original Schrödinger's interpretation of wave function is recalled.

3. Pierwsza metoda wyprowadzenia równania Schrödingera

Na samym początku chcielibyśmy zwrócić uwagę na fakt, że w mechanice klasycznej bardzo ważne zastosowanie mają funkcje jednoznaczne (¹).

I tak o torze ruchu cząstki klasycznej zakłada się, że jest to funkcja jednoznaczna, ciągła i różniczkowalna co najmniej dwukrotnie. Właśnie jednoznaczność tej funkcji odpowiada za matematyczne wyrażenie faktu, że w danej chwili czasu t cząstka może znajdować się tylko w jednym położeniu wskazanym przez wektor r(t) (²).

Z kolei o funkcji działania za [1] przyjmujemy, że jest to następująca całka

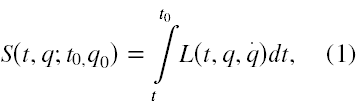
liczona wzdłuż krzywej wyznaczonej z równań Lagrange’a lub z równań Hamiltona, przechodząca przez punkt (t₀; q₀), który uważamy za początkowy oraz przez punkt (t; q), który uważamy za zmienny i która jest jednoznaczną funkcją współrzędnych tych punktów. Można wykazać [1], że definicja funkcji działania (1) jest równoważna zdefiniowaniu tej funkcji poprzez równanie Hamiltona-Jacobiego (³).

Po tym wstępie mającym na celu usystematyzowanie pojęć przechodzimy do analizy rozumowania Schrödingera. Za punkt wyjścia swojego wyprowadzenia przyjął on w [2] równanie Hamiltona-Jacobiego dla przypadku, gdy czas nie występuje jawnie w funkcji Hamiltona

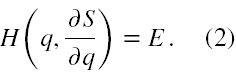
Wyraża to fakt, że układ jest izolowany, niezaburzony przez zewnętrzne źródła oddziaływań. Dalej założył on, że zmienne w rozwiązaniu równania (2) są separowalne i da się go przedstawić jako sumę funkcji, z których każda jest funkcją tylko jednej spośród niezależnych zmiennych q (⁴).

1. Jako pierwszy krok prowadzący do mechaniki kwantowej wprowadził założenie, że funkcję działania S da się wyrazić jako funkcję nowej niewiadomej funkcji ψ w myśl wzoru (⁵)

   

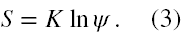
   Ponadto w konsekwencji autor przyjął, że nowa niewiadoma musi się dać przedstawić jako iloczyn odpowiednich funkcji zależnych od pojedynczych współrzędnych. Z kolei o stałej K zauważył, że musi ona być wprowadzona na podstawie analizy wymiarowej, a zatem powinna mieć wymiar działania. W ten sposób zamiast równania (2) otrzymujemy równanie

   

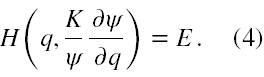
   W tym miejscu musimy przerwać referowanie postępowania Schrödingera i dokładnie przeanalizować ten pierwszy krok.

   Powstaje oczywiste pytanie, skąd pomysł na wzór (3)? Odwróćmy zależność (3) i mamy

   

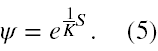
   Jeżeli przyjmiemy, że stała K = ħ/i (⁶), to odpowiedź jest oczywista, że Schrödinger odgadł to podstawienie dzięki analizie funkcji falowej zaproponowanej przez Louis’a de Broglie’a. Jeżeli cząstka klasyczna porusza się ruchem jednostajnym prostoliniowym, czyli jej funkcja działania to S = p·r − Et, wtedy ψ według (5) sprowadza się do funkcji falowej cząstki swobodnej. Niestety, funkcja działania S zdefiniowana poprzez wzór (3) nie jest jednoznaczna (⁷).

2. W drugim kroku Schrödinger ograniczył się do zagadnienia nierelatywistycznego w polu Coulomba (atom wodoru), gdzie funkcja Hamiltona ma postać

   

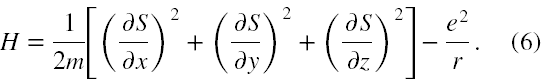
   Wstawił tę funkcję do (4) dokonując jednoczesnej zamiany ∂S/∂q → K/ψ·∂ψ/∂q, przeniósł wszystkie wyrazy na lewą stronę oraz wymnożył całe równanie stronami przez 2mψ²/K² i otrzymał

   

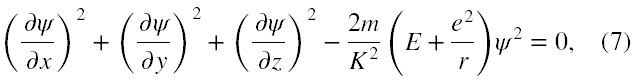
   gdzie oczywiście e - ładunek elektronu, m - masa elektronu, r ² = x ² + y ² + z ² .

   Przeanalizujmy drugi krok Schrödingera. Przyjmijmy za punkt wyjścia nie wzór (3), a wzór (5). Widzimy z własności funkcji eksponencjalnej, że ψ jest jednoznaczną funkcją S, a skoro ta funkcja jest jednoznaczną funkcją (t; q) , więc również i ψ jest jednoznaczną funkcją tych zmiennych (⁸).Po drugie, skoro S jest określona wyłącznie na torze ruchu cząstki (a nie także na torach ruchów porównawczych), więc i ψ istnieje tylko na torze ruchu cząstki.

   Po drugie, przypomnijmy, że w przypadku równania (2) funkcja działania ma postać S = Š(q) − Et + C. Używając wzoru (5) widzimy, że funkcja falowa w tym przypadku ma postać

   

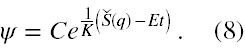
   Równanie (7) nie zależy jawnie od czasu, jest słuszne dla dowolnej chwili czasu t. Jeżeli do (7) podstawimy (8), to z powrotem otrzymamy równanie Hamiltona - Jacobiego na funkcję działania Š(q) dla ruchu elektronu w atomie wodoru. A więc na razie nie wyszliśmy poza ramy mechaniki klasycznej.

3. W trzecim kroku Schrödinger potraktował całą lewą stronę równania (7) jako nową funkcję, czyli

   

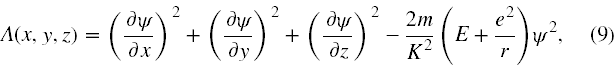
   która teraz niekoniecznie musi być równa 0 i przy jej pomocy sformułował następujący problem wariacyjny

   

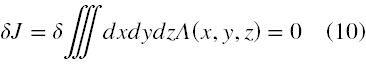
   na funkcję ψ. Przeanalizujmy dokładnie trzeci krok Schrödingera. Wprowadzone tu przez niego założenia są sprzeczne z mechaniką klasyczną.

   Po pierwsze, wyobraźmy sobie dla kontrastu, że całkujemy funkcję Λ(x,y,z) = Λ(x(t),y(t),z(t)) po czasie, wzdłuż toru ruchu, w pewnym przedziale czasu (t₀,t). Na bazie mechaniki klasycznej całka ta jest równa 0. Całkowanie odbyło się dla wybranych położeń x,y,z, tylko tych dostępnych klasycznie.

   Przeciwnie, w postępowaniu Schrödingera całkujemy funkcję Λ(x,y,z) po wszystkich możliwych położeniach, również tych niedostępnych klasycznie, dla których wartość tej funkcji jest różna od zera. Zatem i całka ta jest na ogół różna od zera.

   Problem wariacyjny (10) prowadzi do takiego poprawienia funkcji falowej ψ, aby całka z funkcji Λ(x,y,z) przyjęła wartość ekstremalną, oczywiście niekoniecznie równą zero.

   Po drugie, przypomnijmy, że ruch cząstki klasycznej też można opisać przy pomocy zasady wariacyjnej. Wynika ona z zasady najmniejszego działania Hamiltona, gdzie wariowany funkcjonał to działanie opisane wzorem (1).

   Po trzecie, patrząc teraz per analogia można dojść do wniosku, że skoro rozwiązując klasyczny problem wariacyjny otrzymujemy dla cząstki klasycznej zbiór dozwolonych dla niej położeń, to rozwiązując kwantowy problem wariacyjny otrzymujemy również, tym razem dla cząstki kwantowej, zbiór jej dozwolonych położeń.

   Po czwarte, dla cząstki klasycznej otrzymujemy zbiór dozwolonych położeń sparametryzowanych czasem w ten sposób, że cząstka porusza się wzdłuż krzywej.

   Dla cząstki kwantowej otrzymujemy tylko zbiór dozwolonych położeń (tam gdzie ψ istnieje i jest różne od zera), nie otrzymujemy żadnych informacji jaka jest kolejność czasowa zajmowania położeń, bo równanie (10) nie zależy od czasu. Nie wiemy nawet, czy cząstka porusza się wzdłuż jakiejś krzywej, czy też co jest bardziej prawdopodobne może przeskakiwać z położenia do położenia w sposób nieciągły, a może nawet zajmować kilka położeń na raz.

4. W czwartym kroku Schrödinger zgodnie z [3] rozwiązał problem wariacyjny (10) i w konsekwencji otrzymał swoje stacjonarne równanie w formie

   

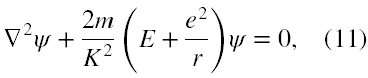
   z warunkiem, że funkcja falowa ψ musi się zerować na granicy obszaru całkowania we wzorze (10). Oznacza to, że faktyczne fizyczne funkcje falowe muszą znikać w nieskończoności.

Na koniec podsumujmy wyprowadzenie Schrödingera poprzez zauważenie faktu, że równanie (11) ma o wiele szersze znaczenie niż wzór (5) użyty w wyprowadzeniu. Analizując znane, choćby z podręczników mechaniki kwantowej, rozwiązania równania (11) dla różnych sytuacji fizycznych dochodzimy do wniosku, że rzeczywiste funkcje falowe na ogół nie mają postaci (5) za wyjątkiem dwóch szczęśliwych przypadków.

Pierwszy z nich to przybliżenie Wentzel-Kramers-Brillouin [4], gdzie wprawdzie funkcja falowa ma postać (8), ale Š(q) nie jest klasyczną funkcja działania. A drugi, to wspomniany wyżej przypadek cząstki swobodnej.

4. Interpretacja funkcji falowej według Schrödingera

W pracy [5], ostatniej z jego cyklu "Quantisierung als Eigenwertproblem", w paragrafie 7 Schrödinger podaje swoją interpretację funkcji falowej.

Nie byłoby w niej nic nadzwyczajnego, gdyby nie fakt, że nie została ona przyjęta jako poprawna przez ogół fizyków. Uznali oni z czasem natomiast jako prawidłową konkurencyjną interpretację opracowaną przez Borna. Co więcej Schrödinger nigdy się z tym faktem nie pogodził, ale oddajmy głos Bornowi [6].

"Schrödinger sądził, że jego falowa teoria umożliwi powrót do deterministycznej klasycznej fizyki. On zaproponował (i ostatnio swoją propozycję podtrzymał na nowo ...), aby całkowicie zrezygnować z posługiwania się wizją cząstek i zamiast mówienia o elektronach jako cząstkach traktować je jako ciągły rozkład gęstości |ψ|² (lub gęstości ładunku elektrycznego e|ψ|²)."

W podobnym tonie wypowiedział się A. Pais w [7], gdzie wskazał, że powodem tego faktu było to, iż Schrödinger uważał, że wynikające z jego niestacjonarnego równania równanie ciągłości (12)

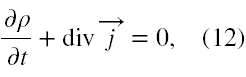
wiążące ze sobą ρ = ψ^∗ψ oraz j = (ħ/2im)[ψ^∗∇ψ - ψ∇ψ^∗] powinno być utożsamiane z zasadą zachowania ładunku elektrycznego.

W swojej pracy Schrödinger szeroko posługuje się pojęciem heurystycznej hipotezy o elektrodynamicznym znaczeniu pola skalarnego ψ, ale oprócz tego wprowadza nową ideę. Zacytujmy tu autora (uwspółcześniliśmy oznaczenia).

ψ^∗ψ jest pewnego rodzaju funkcją wagową w przestrzeni konfiguracyjnej układu. Mechaniczno-falowa konfiguracja układu jest superpozycją wielu, ściśle mówiąc wszystkich, dopuszczalnych kinematycznie punktowo-mechanicznych konfiguracji. Stąd każda punktowo-mechaniczna konfiguracja daje wkład do prawdziwej falowo-mechanicznej konfiguracji z pewną wagą, która jest dana dokładnie poprzez ψ^∗ψ. Jeśli lubimy paradoksy, to możemy powiedzieć, że system istnieje jakby był jednocześnie we wszystkich położeniach kinematycznie wyobrażalnych, ale nierówno silnie we wszystkich.

Śledząc rachunki Schrödingera można ustalić, że jego hipoteza bierze swój początek w pracy [8] o równoważności mechaniki macierzowej i falowej, w której analizował sens fizyczny, jak byśmy to dzisiaj powiedzieli elementów macierzowych operatora zaburzenia opisujących przejścia kwantowe między stanami atomu i doszedł do wniosku, że eψ^∗ψ opisuje rozkład gęstości ładunku elektronowego w atomie.

Dla porównania Born analizując procesy rozproszeniowe doszedł do wniosku, że ψ^∗ψ opisuje gęstość prawdopodobieństwa znalezienia cząstki kwantowej w konkretnym punkcie przestrzeni. Jednak tu należy podkreślić, że analizował on biegnące stany swobodne, a nie stacjonarne stany związane.

W tym miejscu musimy podkreślić, że nie przypadkiem analizowaliśmy pierwszą metodę wyprowadzenia stacjonarnego równania Schrödingera, albowiem doszliśmy do wniosku, że przy jej pomocy możemy coś nowego wnieść do tego sporu o interpretację funkcji falowej. Wróćmy do wzoru (10) i wniosków z niego wypływających.

1. Interpretację Schrödingera możemy przypisać do sytuacji, gdy "tor ruchu" cząstki kwantowej jest funkcją wieloznaczną, czyli w wybranej chwili czasu t znajduje się ona po trochu w każdym położeniu r(t), w którym funkcja falowa ψ przyjmuje wartość niezerową.

2. Interpretację Borna powiązalibyśmy z sytuacją, gdy cząstka kwantowa przeskakuje w sposób nieciągły z położenia na położenie.

Podsumowując widzimy, że w sposób naturalny pojawia się pytanie, czy istnieje jakaś parametryzacja od czasu t (chociażby nie była ona funkcją ciągłą) położeń dozwolonych dla cząstki kwantowej w związanym stanie stacjonarnym? Jak widać z pierwszego wyprowadzenia równania Schrödingera aparat mechaniki kwantowej nie zawiera odpowiedzi na to pytanie. Będziemy powracać do tego problemu w dalszych częściach naszego artykułu.

UWAGI

(¹) Funkcja jest jednoznaczna, jeżeli każdemu elementowi x jej dziedziny odpowiada dokładnie jeden element y jej przeciwdziedziny

(²) W tym artykule konsekwentnie pogrubienie oznacza symbol wektora.

(³) Niezależnie czy funkcja działania S(t; q) jest wyznaczona w myśl wzoru (1), czy też bezpośrednio za pomocą równania Hamiltona-Jacobiego istnieje ona tylko dla tych punktów (t; q), które leżą na rzeczywistym torze ruchu naszej cząstki klasycznej, natomiast nie jest ona określona dla jakiegokolwiek punktu toru ruchu porównawczego (bo na nim nie są spełnione równania Lagrange’a, czy Hamiltona).

(⁴) Zmienna q reprezentuje zbiór zmiennych (x,y,z).

(⁵) Chociaż Schrödinger nie nazwał swojej funkcji, to my nazwiemy ją konsekwentnie od samego początku funkcją falową. Chodzi nam o to, aby nie było wątpliwości jakiej funkcji własności badamy.

(⁶) To trochę dziwne, ale Schrödinger nie posługiwał się konsekwentnie, od samego początku liczbami zespolonymi.

(⁷) Zwróćmy uwagę, że rzeczywiste funkcje falowe, zwłaszcza dla stanów swobodnych są funkcjami okresowymi, a więc niemonotonicznymi. Tym samym definicja (3) nie jest równoważna (1), albowiem funkcja odwrotna funkcji niemonotonicznej nie musi być jednoznaczna. Wynika to z faktu, że tylko gdy funkcja y = f (x) jest określona, ściśle rosnąca (malejąca) i ciągła w pewnym przedziale, to tylko wtedy mamy pewność, że w odpowiednim przedziale jej przeciwdziedziny istnieje jednoznaczna funkcja odwrotna x = g(y), także monotonicznie rosnąca (malejąca) i ciągła.

(⁸) Tak naprawdę, to obie funkcje muszą mieć lepsze własności. Funkcja S musi być różniczkowalna, a ψ dwukrotnie różniczkowalna względem zmiennych położeniowych.

LITERATURA

[1] R. S. Ingarden, A. Jamiołkowski, Mechanika Klasyczna, PWN, Warszawa-Poznań 1980.

[2] E. Schrödinger, Quantisierung als Eigenwertproblem I, Annalen der Physik, 79, 361 (1926).

[3] I. M. Gelfand, S. W. Fomin, Rachunek Wariacyjny, PWN, Warszawa 1979.

[4] L. Schiff, Quantum Mechanics, McGraw-Hill, New York, 1968.

[5] E. Schrödinger, Quantisierung als Eigenwertproblem IV, Annalen der Physik, 81, 109 (1926).

[6] M. Born, The statistical interpretation of quantum mechanics, Nobel Lecture (1954).

[7] A.Pais, Max Born's Statistical Interpretation of Quantum Mechanics, Science, 218, 1193 (1982).

[8] E. Schrödinger, On the Relation between the Quantum Mechanics of Heisenberg, Born, and Jordan, and that of Schrödinger, Annalen der Physik, 79, 734 (1926).