Rozwiązanie równania Diraca w jednorodnym polu elektrycznym - część 2

Szczegóły

Kategoria: Równanie Diraca

Opublikowano: środa, 24, luty 2016 17:19

Autor : Janusz Szcząchor

Exact solutions of the Dirac equation in a homogeneous electric field

Abstract: Solutions of the Dirac wave equation representing an electron and a positron moving in a homogeneous electric field are obtained. The spinor representation is applied. The wave functions are nonstationary. D’Alembert’s method of solving second order partial differential equations is used. Nonexplicit expressions of energy and momentum are obtained. The expressions are relativistically correct.

Rozwiązanie - ciąg dalszy

§2. Ruch ładunków w jednorodnym polu elektrycznym

W celu przygotowania dalszych obliczeń przypomnijmy jak się zachowują poszczególne ładunki w jednorodnym polu elektrycznym i obliczmy potencjał takiego pola. Posłużmy się w tym celu poniższym rysunkiem. Pamiętajmy, że ładunkiem próbnym jest ładunek dodatni. Dlatego może nim być pozyton.

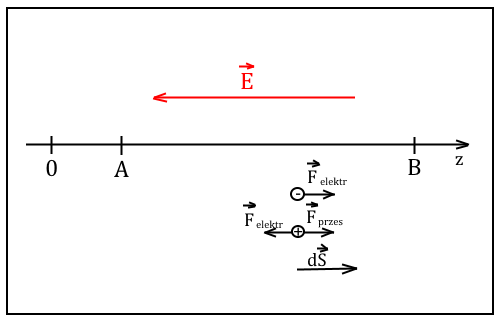
Jednorodne pole elektryczne o zwrocie jak na rysunku przesuwa ładunek ujemny do + ∞, a dodatni do 0. Działając siłą F_przes na ładunek pozytonu (znak +) wykonujemy pracę dodatnią nad nim. Załóżmy, że przesunęliśmy ładunek ten od punktu A do B, czyli wykonaliśmy pracę

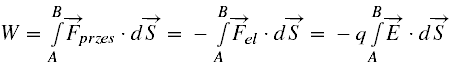
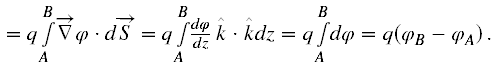
Ponieważ dla pozytonu q > 0 i W > 0, więc φ_B > φ_A.

Skoro pole elektryczne jest liniowe, to zgodnie z powyższym rysunkiem E = −εk, gdzie ε > 0, a ponieważ E = - grad φ, więc φ = εz w tym przypadku. Żeby nie było niejasności przypominam, że w równaniu Diraca oznaczałem φ jako A₀.

§3. Niestacjonarne rozwiązania równania Diraca w jednorodnym polu elektrycznym

A zatem przechodzimy do rozwiązywania układu równań składającego z równania II rzędu na φ (13) oraz równania I rzędu na χ w (11). Skoro pole elektryczne skierowaliśmy wzdłuż osi z, więc nie ma ono wpływu na pęd cząstki diraca wzdłuż osi x i y. Zatem możemy przyjąć, że pędy cząstki wzdłuż tych osi są równe 0 bez utraty szczegółów fizycznych. Wtedy funkcja falowa φ w (13) będzie zależeć tylko od dwóch zmiennych z i x⁰. Podstawiając jawnie wskazane wyżej postacie pola i potencjału elektrycznego oraz przyjmując, że poszukujemy rozwiązań dla elektronu, to jest e → −e otrzymujemy do rozwiązania następujący układ równań

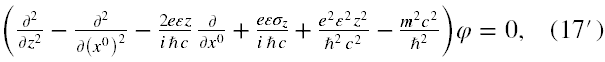
Zgodnie z podaną powyżej interpretacją równania Diraca powyższa para równań (17) dla elektronu powinna mieć w wybranym przez Nas polu elektrycznym dwa rozwiązania, każde o innym znaku energii. Nie będę ukrywał, że powyższy układ równań można jawnie rozwiązać. Również nie wdając się w matematyczne szczegóły zawarte w [13] i [14], do których to pozycji odsyłam zainteresowanych wyjaśniam, że równanie (17’) jest równaniem hiperbolicznym, a rozwiązuje się go metodą d’Alemberta dokonując następującej zamiany zmiennych

λ = z - x⁰, (18')

oraz

η = z + x⁰. (18'')

Jakobian takiego przekształcenia J = D(λ,η)/D(z,x⁰) = 2, a zatem jest różny od zera dla dowolnych z i x⁰, czyli odwzorowanie (18' i 18'') dokonujące zamiany zmiennych przekształca wzajemnie jednoznacznie całą płaszczyznę na siebie.

Teraz musimy przeliczyć wszystkie operatory różniczkowe i stare zmienne na nowe zmienne. Te proste, choć nudne rachunki prowadzą do wzorów

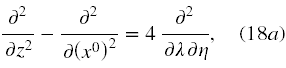
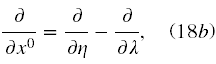
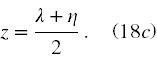
Równanie (17’) w nowych zmiennych przyjmuje postać

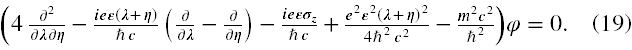
Podzielmy stronami (19) przez 4 i wprowadźmy następujące oznaczenia celem pogrupowania stałych:

α = eε/4ħc ,

β = m²c²/4ħ².

Następnie tak otrzymane równanie podzielmy stronami przez α i dokonajmy jeszcze jednej upraszczającej zamiany zmiennych

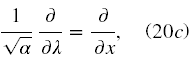
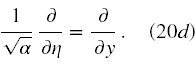
W ostateczności otrzymujemy następujące równanie różniczkowe II rzędu na bispinor elektronowy φ

Bispinor φ ma dwie składowe, ale specjalnie ustawiliśmy pole elektryczne wzdłuż osi z, aby otrzymać w równaniu (21) diagonalną macierz σ_z. Ma ona w pozycji σ₁₁ → 1, w σ₂₂ → -1, a w pozostałych 0. W dalszym ciągu ograniczymy się do rzutu spinu w górę, czyli położymy, że bispinor φ ma na pierwszej pozycji funkcję φ¹, a na drugiej 0. Dla rzutu spinu w dół postępuje się odwrotnie.

Teraz możemy wrócić do równania (17“) i dokonać w nim analogicznych przekształceń i uproszczeń. Otrzymamy stąd równanie na χ¹ w parze z równaniem na φ¹. Tym samym będziemy mieli do rozwiązania następujący układ równań, przy czym musimy wprowadzić jeszcze jedną stałą postaci ω = mc/2ħ√α = (β/α)^1/2.

Przystępujemy zatem do rozwiązywania równania (22’). Wprawdzie według [13] istnieje ogólna metoda rozwiązywania równań hiperbolicznych zwana metodą Riemanna, która uzupełniona metodą kolejnych przybliżeń pozwala rozwiązać dowolne takie równanie o zmiennych współczynnikach, jednak postać rozwiązania ma tak ogólną formę, że jest bardzo trudna do wykorzystania w naszym przypadku.

Jednak w mechanice kwantowej układów wieloelektronowych istnieje metoda rozwiązywania równań Hartree-Focka, której algorytmu poważna część nie polega na całkowaniu, a na umiejętnym odgadnięciu ogólnej postaci rozwiązania i wprowadzeniu do niego parametrów, które będąc właściwie funkcjami będą szukane w całkowaniu. Ta metoda całkowania równań kwantowych nazywa się metodą funkcji próbnych.

A zatem spróbujemy znaleźć tak dobrze dobraną funkcję próbną, która na tyle uprości nasze równanie, że będzie możliwe jego scałkowanie. Po dłuższym przyjrzeniu się równaniu (22’) można dojść do wniosku, że dobra będzie funkcja próbna o nastepującej postaci

φ¹ = e^{i{a(x+y)2/2 +bf(x,y)}},

gdzie a i b to stałe, które możemy odpowiednio dobrać, a f(x,y) to nieznana funkcja zmiennych x i y, którą trzeba znaleźć.

Po wstawieniu do (22’) tak postulowanej postaci rozwiązania i dokonując obliczeń dochodzimy do wniosku, że musimy położyć a = 1, aby zredukowała się dostatecznie duża ilość wyrazów. W końcu otrzymujemy następujące równanie

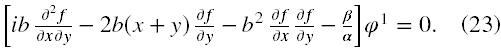
Wyrażenie w nawiasie kwadratowym jest funkcją zespoloną, a zatem jest ona zerem, gdy odpowiednio zerują się jego części rzeczywista i urojona. Co do części urojonej to musimy rozwiązać następujące równanie

∂²f/∂x∂y = 0.

Jest to inna postać równania falowego, a jego rozwiązanie jest proste, funkcja f(x,y) będąca rozwiązaniem musi mieć postać

f(x,y) = g(x) + h(y). (24)

Co do równania dla części rzeczywistej to przepiszmy je do bardziej zwartej postaci, która ułatwi dalszą analizę i wygląda następująco

Skoro (24) funkcja h ma zależeć tylko od y, to równanie różniczkowe na tę funkcję nie może zawierać zmiennej x i na odwrót równanie na funkcję g z tego samego powodu nie może zawierać zmiennej y, oba mogą co najwyżej zawierać jakieś stałe. Zatem ∂f/∂y równe jest dh/dy oraz ∂f/∂x jest równe dg/dx. Stąd do rozwiązania otrzymujemy dwa równania

2x + bdg/dx = C , (a)

oraz

(2y + C)bdh/dy + β/α = 0 , (b)

gdzie C, to pewna stała o charakterze stałej całkowania. Obydwa równania całkuje się już w sposób podręcznikowy, a ich rozwiązania to

g(x) = (−x² + Cx + C₁)/b , (a)

h(y) = [−β/2αb]ln|2y + C| + C₂. (b)

Tak otrzymane funkcje g(x) i h(y) można wstawić do rozwiązania na φ¹. Zauważymy wtedy, że znika zależność od b, stałe C₁ i C₂ można połączyć w jedną stałą C₁ i wyłączyć ją jako C₁ przed eksponent, będzie ona spełniać rolę stałej normującej. Ostatecznie otrzymujemy rozwiązanie w postaci

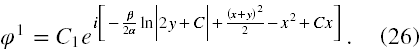
Pozostaje policzyć χ¹. W tym celu musimy policzyć pochodną φ¹ po ∂y, czyli praktycznie pochodną cząstkową jej wykładnika. Po redukcji wyrazów podobnych i uproszczeniu stałych zgodnie z (22“) otrzymujemy

Zatem rozwiązaniem układu równań (22) jest poniższy bispinor

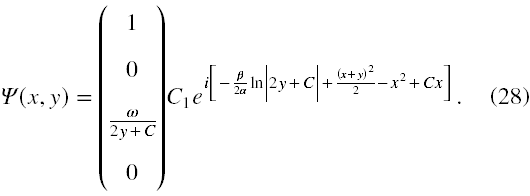
§4. Analiza otrzymanego rozwiązania niestacjonarnego

Otrzymana postać bispinora elektronowego (28) w pomocniczych zmiennych x i y niewiele nam mówi poza tym, że rzeczywiście strukturą przypomina on elektronowy bispinor swobodny dla rzutu spinu w górę [5]. Dlatego musimy przeliczyć tak otrzymane rozwiązanie z powrotem na zmienne z i x⁰, a następnie policzyć ile wynoszą, o ile takowe istnieją, wartości własne energii i pędu takiej cząstki Diraca.

Przejścia od zmiennych x i y do z i x⁰ dokonujemy według następujących zależności

x = (z − x⁰)√α ,

y = (z + x⁰)√α

i otrzymujemy, że

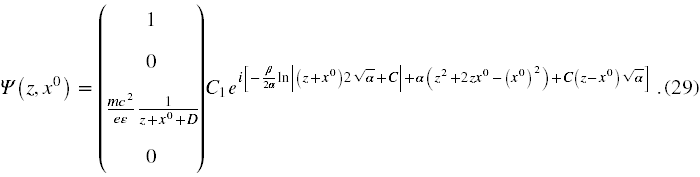
Tutaj stała D = C/(2√α).

Należy teraz zastanowić się, czy takie rozwiązanie wstawione do równań własnych na energię i pęd da jakieś sensowne wartości?

Charakter wykładnika w (29) - czysto urojony - nasuwa podejrzenie, że rozwiązanie to powinno opisywać cząstkę swobodną znajdującą się w zewnętrznym polu. Dla takiego przypadku klasyczna teoria Lagrange'a i Hamiltona wskazuje, że pęd tej cząstki, to pęd kinetyczny, który w mechanice kwantowej jest opisany operatorem o poniższej postaci [15]

q^μ = p^μ − eA^μ.

Eksponent w (29) daje sensowną rzeczywistą wartość własną, niestety składowe bispinora będą źródłem części urojonych energii i pędu. Wiadomo jednak, chociażby z uniwersyteckich kursów mechaniki kwantowej, że interpretację jako energia ma tylko część rzeczywista wartości własnej operatora energii. Uważamy, że podobnie powinno się postąpić w przypadku pędu. Patrz także [16,17].

Ponieważ tylko składowa A⁰ jest różna od zera, więc tylko operator energii ma zmodyfikowaną postać. A zatem liczymy i otrzymujemy, że wartość własna operatora energii dla otrzymanego rozwiązania równania Diraca w jednorodnym polu elektrycznym, to

Re {iħ∂Ψ/∂t}/Ψ + eεz, (30a)

czyli

Natomiast wartość własna operatora pędu dla tegoż rozwiązania to

Re {(ħ/i)∂Ψ/∂z}/Ψ (31a),

czyli

Wzory te zawierają ponownie stałą: D = C/(2√α). Wyrażenia (30a) i (31a) należy traktować w sposób oczywiście symboliczny.

Przez bezpośrednie podstawienie można sprawdzić, że tak otrzymane wartości własne energii (30) i pędu (31) spełniają znaną relację

E² = p²c² + m²c⁴,

co potwierdza słuszność Naszego postulatu co do sposobu interpretacji części urojonych wartości własnych operatorów energii i pędu.

Postać bispinora (29) można przekształcić do bardziej eleganckiej postaci. Wystarczy zauważyć, że

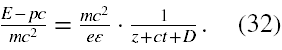
Wtedy bispinor (29) przyjmie postać (33), identyczną co do formy funkcjonalnej z bispinorem swobodnym, wzór (29) w [5]

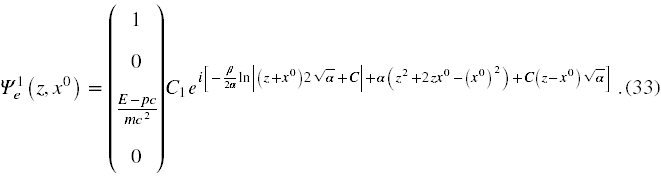
Wektor ten oznaczyłem wskaźnikiem górnym ‘1’ dla oznaczenia, że chodzi o rzut spinu w górę, a ‘e’ - dla oznaczenia, że chodzi o rozwiązanie dla elektronu.

Dla rzutu spinu w dół mamy do rozwiązania następujący układ równań

Postępując zgodnie z powyżej przedstawionymi metodami rachunkowymi otrzymamy następujące rozwiązanie

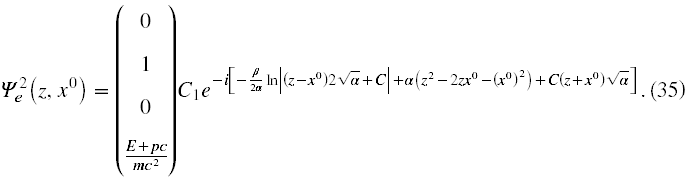
Tutaj jednak wartości własne energii i pędu, to odpowiednio

oraz

Tak otrzymana postać bispinora (35) ponownie bardzo przypomina rozwiązanie swobodne.

Jeśli chodzi o interpretację tak otrzymanych wyników, to odkładam to do kolejnego artykułu.

LITERATURA

[1] J. D. Bjorken, S. D. Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985, §1.4 .

[2] W. B. Bierestecki, E. M. Lifszyc, L. P. Pitajewski, Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §32.

[3] I. Białynicki-Birula, Z. Białynicka-Birula, Elektrodynamika kwantowa, PWN, Warszawa 1974, §16.

[4] J. D. Bjorken, S. D. Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, PWN, W-wa 1985, rozdział 5 .

[5] J. Szcząchor, Metody rozwiązywania równania Diraca - Część 1.

[6] W. Pogorzelski, Analiza matematyczna, Tom IV, PWN, Warszawa 1956, część 10, §24.

[7] L. D. Landau, E. M. Lifszyc, Mechanika Kwantowa - teoria nierelatywistyczna, PWN, Warszawa 1979, rozdział III, §24. Ruch w polu jednorodnym.

[8] A. Calogeracos, N. Dombey, History and Physics of the Klein Paradox, arXiv:quant-ph/9905076v1.

[9] O. Klein, Z. f. Physik 53, 157 (1929).

[10] F. Sauter, Z. f. Physik 69, 742-764(1931), Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs.

[11] M. S. Plesset, The Dirac Electron in Simple Fields, Physical Review 41, 278 (1932).

[12] J. Szcząchor, Metody rozwiązywania równania Diraca - Część 2.

[13] W. Pogorzelski, Analiza matematyczna, Tom IV, PWN, Warszawa 1956, część 10, §4,§21-23,§25.

[14] W. I. Smirnow, Matematyka wyższa, Tom II, PWN, Warszawa 1963, rozdział VII, §17.164.

[15] W. B. Bierestecki, E. M. Lifszyc, L. P. Pitajewski, Relatywistyczna teoria kwantów,Tom 1, PWN, Kraków 1972, §40.

[16] J. Szcząchor, On the wave function of relativistic electron moving in a uniform electric field.

[17] A. I. Nikishov, V. I. Ritus, Quantum Processes in the Field of a Plane Electromagnetic Wave and in a Constant Field. I, Soviet Physics JETP 19, (1964) 529.