Jak interpretować ujemną energię cząstek kwantowych?

Szczegóły

Kategoria: Fizyka szkolna

Opublikowano:piątek, 15 listopad 2019 20:21

Autor : Janusz Szcząchor

§1 Wstęp

Analizujemy tutaj dwa przypadki, kiedy cząstka kwantowa typu elektron może mieć ujemną energię całkowitą. Pierwszy to przypadek przyciągającego centrum, kiedy mamy do czynienia z uwięzieniem cząstki w polu siły. Drugi to problem rozwiązań równania Diraca o ujemnej energii.

Jakiś czas temu trafiła w moje ręce pozycja „Krótka historia Stephena Hawkinga“ Kitty Ferguson [1]. Nie mam czasu na czytanie książek beletrystycznych o nauce, ale tę wyjątkowo otrzymałem w prezencie za udział w programie radiowym „Klub ludzi ciekawych wszystkiego“ w PR2. Była akurat audycja o współczesnych teoriach grawitacji, w tym o kwantowej grawitacji.

W tej sytuacji nie było sposobu, żeby nie przeczytać książki. Co do jej treści merytorycznej (czyli życiorysu Stephena Hawkinga) trudno mieć zastrzeżenia, ale zaintrygowała mnie próba autorki wyjaśnienia czym jest promieniowanie Hawkinga przy pomocy istnienia cząstek kwantowych o ujemnej energii, którą podjęła na stronach 99-102.

Jako dowód weźmy pod uwagę taki fragment - „Hawking doszedł do wniosku, że na horyzoncie zdarzeń czarnej dziury będzie pojawiać się wiele tego rodzaju par cząstek. Pary wirtualnych cząstek pojawiają się i ulegają rozdzieleniu. Zanim zdołają spotkać się ponownie i anihilować, cząstka o ujemnej energii minie horyzont zdarzeń i wpadnie do czarnej dziury. „

Wszystko byłoby dobrze, tylko dlaczego cząstka ma mieć ujemną energię? Poszukałem informacji o autorce i dowiedziałem się, że co do fizyki, to w tej dziedzinie edukację zakończyła na etapie szkoły średniej. Nie wyglądało to dobrze. Autorka jednak przyznaje, że Stephen Hawking bardzo dużo jej tłumaczył z fizyki. Zajrzałem zatem do jego oryginalnej pracy o tym promieniowaniu [2].

Możemy tam przeczytać (w moim tłumaczeniu).

Tuż za horyzontem zdarzeń będą pary wirtualnych cząstek, jedna o ujemnej energii i jedna o dodatniej energii. Cząstka o ujemnej energii jest w rejonie, który jest klasycznie zakazany, ale ona może tunelować przez horyzont zdarzeń do rejonu wewnątrz czarnej dziury, gdzie wektor Killinga, który reprezentuje przesunięcia w czasie jest typu przestrzennego.(...) Zamiast rozważania tunelowania cząstek o ujemnej energii przez horyzont (...) można by je traktować jako cząstki o dodatniej energii przekraczające horyzont (...).

Ale dalej wyjaśnia.

Należy podkreślić, że te obrazy mechanizmów odpowiedzialnych za termiczną emisję (...) są tylko heurystyczne i nie powinny być brane zbyt dosłownie.

Nie pozostaje zatem nic innego jak spróbować wyjaśnić, czy cząstka kwantowa na poziomie co najmniej relatywistycznej mechaniki kwantowej może faktycznie mieć ujemną energię i co to ewentualnie oznacza.

§2 Ujemna energia elektronu w polu elektrostatycznym protonu oraz ciała astronomicznego w polu grawitacyjnym

Ucząc się fizyki spotykamy się po raz pierwszy z możliwością, że energia ciała fizycznego jest ujemna podczas rozpatrywania jego ruchu w polach sił przyciągających. Szczególnie chodzi tu o energię potencjalną w polu grawitacyjnym oraz w przyciągającym polu elektrostatycznym. Typowa sytuacja polega na tym, że źródłem pola jest ciało o na tyle dużej masie w stosunku do masy ciała przyciąganego, że to pierwsze jest prawie nieruchome, a porusza się to drugie.

Celem wyjaśnienia o co w tym chodzi zacznijmy od przedstawienia wykresu energii potencjalnej elektronu w polu przyciągającego go elektrostatycznie protonu traktowanych klasycznie (rys. nr 1).

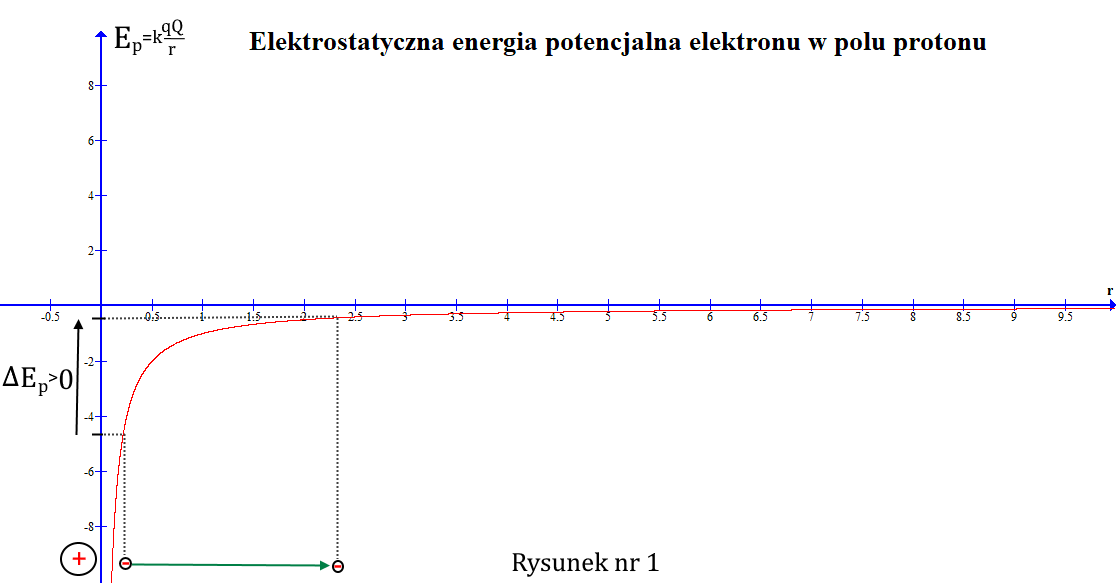
Aby przesunąć elektron od protonu do nieskończoności musimy wykonać nieskończoną pracę przeciwko sile Coulomba. Podobnie, aby przysunąć dodatni pozyton z nieskończoności do protonu też musimy wykonać taką pracę (rys. nr 2).

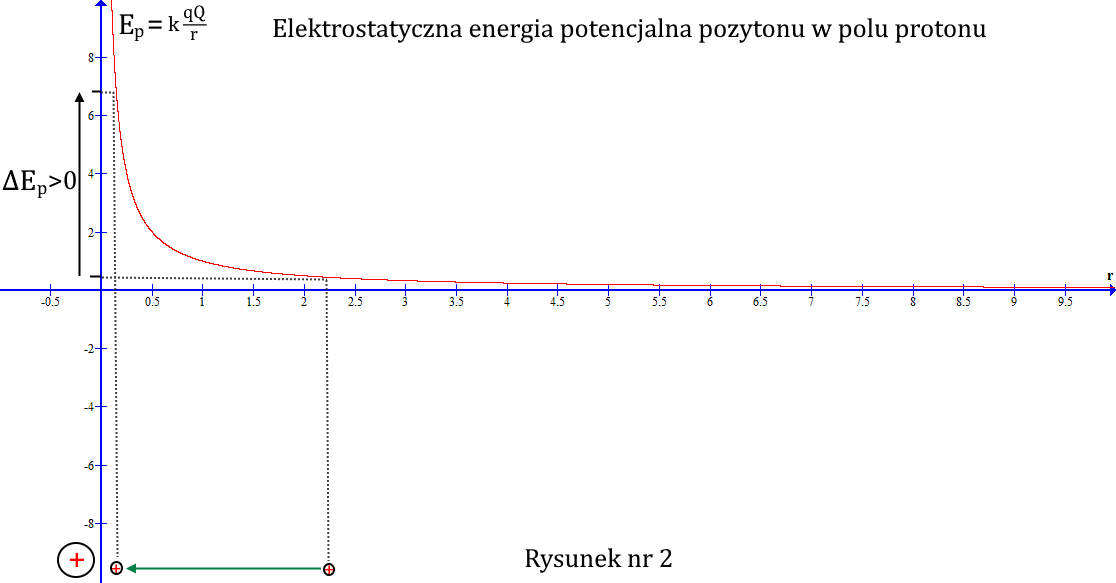
Jednak energia potencjalna musi być wielkością fizyczną uniwersalną i oba przypadki muszą mieścić się w definicji tej samej wielkości. Z przyczyn, o których niżej, wybrano, że elektron w pobliżu protonu ma energię ujemną, a w nieskończoności 0. Z kolei pozyton w pobliżu protonu ma energię potencjalną dodatnią, a w nieskończoności też 0.

W przypadku, gdy między dwoma przyciągającymi się ciałami istnieje znaczna różnica masy oba ciała tworzą układ, w którym lżejsze ciało możemy traktować jako uwięzione przez to cięższe. Aby się wyswobodzić lżejsze ciało musi zdołać się oddalić do nieskończoności. Będzie to możliwe, gdy uzyska ono odpowiedni przyrost energii potencjalnej dzięki pracy sił zewnętrznych, albo swojej energii kinetycznej, którą będzie mogło zamienić na pracę przeciwko siłom pola.

Przyjęcie, że poziom zerowy energii jest minimalną energią, przy której ciało staje się swobodne jest bardzo wygodne z punktu widzenia łatwego rozpoznania, czy ciało jest w stanie związanym, czy swobodnym. Jednak jest to tylko kwestią umowy, bo sens fizyczny ma tylko wykonana praca, czyli zmiana energii potencjalnej, a nie jej wartość bezwzględna. Rozważmy sytuację w polu grawitacyjnym.

Niech ciało astronomiczne pochodzące spoza Układu Słonecznego dysponuje pewną energią kinetyczną. Wpadając w nasz Układ przekracza granicę zera energii potencjalnej tego układu. Energia całkowita tego ciała, to

E_całkowita = E_p + E_k = 0 + E_k > 0. (1)

Jeśli tylko ciało to nie straci energii kinetycznej w wyniku zderzenia z innymi ciałami, to przekształcanie się energii potencjalnej ciężkości w jego energię kinetyczną z jednoczesnym zbliżaniem się ciała do centrum przyciągania nie będzie miało wpływu na losy ciała.

Dzięki zgromadzonemu zapasowi energii kinetycznej ciało mijając centrum Układu będzie w stanie jej kosztem wykonać pracę przeciwko sile przyciągania i w końcu uwolni się.

W ten sposób losy ciała można łatwo przewidzieć sprawdzając, czy w dowolnym punkcie jego toru ruchu ciało to posiada całkowitą energię większą od zera, równą zeru, czy też mniejszą od zera.

§3 Ujemna energia elektronu w teorii atomu Bohra i nierelatywistycznej mechanice kwantowej

Bardzo podobna sytuacja ma miejsce w modelu atomu wodoru Bohra [3].

Na energię elektronu zawartego w tym atomie również składają się jego energia potencjalna w polu jądra atomu, czyli E_p = -e²/4πε₀r oraz energia kinetyczna E_k = mv²/2 (m - to masa elektronu, a właściwie jego masa zredukowana ¹).

Dzięki postulatowi "kwantowemu" Bohra dopuszczającemu tylko te orbity elektronowe, które spełniają specjalny warunek dla momentu pędu elektronu

mvr = nh/2π, (2)

otrzymujemy, że energia całkowita elektronu w atomie wodoru jest dana jako

E_n = - me⁴/8ε₀²h²n² , (3)

a promień dozwolonej orbity elektronowej, to

r_n = ε₀h²n²/πme².  (4)

Z powyższych wzorów doskonale widać, że gdy n ⇾ ∞, to E_n ⇾ 0, a r_n ⇾ ∞.

Równanie Schrödingera [5], służące w nierelatywistycznej mechanice kwantowej do poszukiwania dozwolonych stanów energetycznych atomu wodoru (będących odpowiednikami dozwolonych orbit elektronowych w teorii N.Bohra) ma postać

Eψ = (-h²∇²/8π²μ - ke²/r)ψ,  (5)

gdzie E jest całkowitą energią elektronu, pierwszy człon w nawiasie jest jego energią kinetyczną, a drugi elektrostatyczną energią potencjalna w polu jądra, μ - masa zredukowana elektronu, ψ - funkcja służąca m.in. do obliczenia prawdopodobieństwa znalezienia elektronu.

W wyniku rozwiązania tego równania otrzymujemy dokładnie takie same poziomy energii elektronu jak dane powyżej wzorem (3).

Podsumowując, ujemny znak energii elektronu nadal oznacza jedynie fakt, że elektron w atomie wodoru jest w stanie związanym i może w pewnych warunkach "uwolnić się", i uzyskać całkowitą energię równą 0 J. Jednak proces ten nie prowadzi ani do przemiany elektronu w inną czastkę, ani do kreacji innej cząstki oprócz istniejącego elektronu.

Sytuacja radykalnie się zmieni, gdy do opisu elektronu użyjemy równania Diraca.

§4 Ujemna energia w teorii elektronu Diraca

Jako, że teoria Diraca jest teorią relatywistyczną wypadałoby zrobić najpierw jakiś wstęp. Wskażę tylko najistotniejsze elementy, które będą niezbędne do dalszych rozważań.

W fizyce nierelatywistycznej energię mechaniczną dzielimy na kinetyczną i potencjalną. Jeżeli jednak ciało fizyczne jest swobodne, nie znajduje się w jakimś polu oddziaływań, to jego energia potencjalna jest równa 0. Jeżeli do tego ciało to znajduje się w spoczynku względem jakiegoś układu odniesienia, to również i jego energia kinetyczna jest równa 0 w tym układzie. Wyglądałoby zatem, że ciało fizyczne może mieć energię równą zero, ale nie w fizyce relatywistycznej.

W mechanice relatywistycznej energia całkowita ciała ma postać

E = √(p²c² + m²c⁴). (6)

Zakładając, że prędkość ciała jest mała w stosunku do prędkości światła możemy energię rozwinąć w szereg i mamy

E ≈ mc² + mv²/2 + ... , (7)

gdzie m - to masa spoczynkowa, czyli masa ciała (bezwładna) zmierzona w układzie odniesienia, w kórym ciało to spoczywa.

W 1928 roku Paul Dirac odkrył równanie [6], które wreszcie poprawnie opisywało zachowanie elektronu na poziomie relatywistycznym, a także w sposób naturalny wyjaśniało dlaczego składowa np. zetowa spinu, czyli wewnętrznego moment pędu elektronu jest równa ℏ/2 i jaki to ma wpływ na widmo poziomów energetycznych np. atomu wodoru (²).

W jednej z kolejnych swoich prac [7] Dirac podjął próbę zniwelowania "wady" na jaką "cierpiało" jego równanie, a mianowicie to, że jego równanie dopuszcza przejścia kwantowe elektronu ze stanu o energii +mc² lub wyższej do stanu o energii -mc² lub niższej nawet w nieobecności zewnętrznego pola, a powstała nadwyżka energii o wartości co najmniej 2mc² jest spontanicznie emitowana w formie przynajmniej dwóch kwantów światła, a tym samym nie można ignorować istnienia stanów o ujemnej energii bez wywoływania niejasności co do interpretacji jego teorii.

Dla elektronu w spoczynku i w nieobecności jakichkolwiek pól rozwiązania tego równania przyjmują postacie

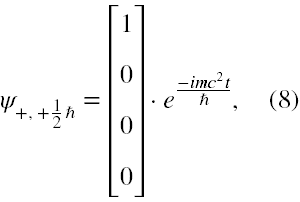
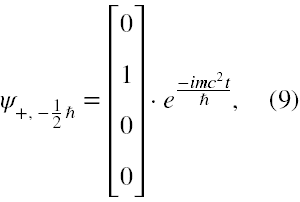
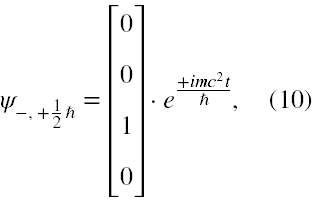
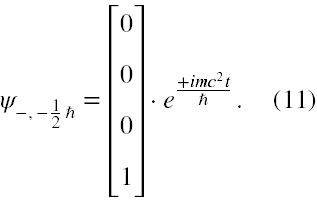
Działając na eksponenty powyższych funkcji operatorem energii całkowitej, czyli iℏ∂/∂t możemy przekonać się, że pierwsze dwie funkcje odpowiadają energii elektronu o wartości +mc², a dwie pozostałe -mc².

Celem rozwiązania powyższej "wady" Dirac skonstatował istotny fakt, ale oddajmy mu głos (w moim tłumaczeniu).

Zbadajmy funkcje falowe reprezentujące stany o ujemnej energii trochę bardziej szczegółowo. Jeśli dokonamy superpozycji pewnej liczby tych funkcji falowych w ten sposób, aby otrzymać pakiet falowy (³), to ruch tego pakietu będzie zachodził wzdłuż klasycznego toru ruchu danego przez Hamiltonian (3) z ujemną wartością E + eA₀. Taki tor ruchu, jak łatwo pokazać, to dopuszczalny tor ruchu dla zwykłego elektronu (o dodatniej energii) poruszającego się w polu elektromagnetycznym o przeciwnym znaku, lub dla elektronu o ładunku +e (i dodatniej energii) poruszającego się w niezmienionym polu elektromagnetycznym.

Powyższy wniosek zawiera istotną sugestię, że w grę wchodzi istnienie nowej cząstki, tylko jakiej? Zapewne domyślarz się, że chodzi o pozyton. W 1931 roku, na samym wstępie pracy [9] Dirac uznał, że chodzi o antyelektron (wówczas jeszcze nieodkryty), cząstkę o tej samej masie co elektron, identycznym spinie, ale o ładunku elektrycznym przeciwnego znaku. Zanim jednak do tego doszło było wiele zwrotów akcji, o czym możesz szerzej przeczytać w cytowanej wyżej książce Weinberga oraz w [10] o odkryciu w roku 1932 antyelektronu od strony doświadczalnej.

Niestety, odkrycie pozytonu nadal nie rozwiązuje problemu. Dlaczego? Przyjrzyjmy się bliżej równaniu Diraca w zewnętrznym polu elektromagnetycznym. Oto ono

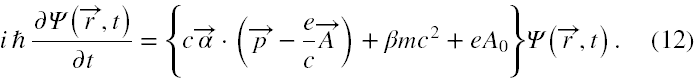
Nie zorientowanym wyjaśniam, że z dobrym przybliżeniem potencjał wektorowy A jest źródłem pola magnetycznego oraz zmiennego pola elektrycznego, a potencjał skalarny A₀ (to ten potencjał znany z kursu fizyki w szkole) jest źródłem pola elektrostatycznego.

Równanie (12), to faktycznie dwa równania. Jeżeli za e podstawimy -|e|, to otrzymamy równanie dla elektronu, a jeżeli |e| (czyli faktycznie nic nie zrobimy), to będziemy mieli równanie dla pozytonu.

Jeżeli teraz w obu równaniach za oba potencjały podstawimy 0 (czyli wyłączymy oba pola elektryczne i magnetyczne), to z obu równań zniknie ładunek elektryczny i równania te nie będą się niczym różnić, będą identyczne dla obu cząstek. Będą to równania dla obu cząstek w stanie swobodnym i obie cząstki będą miały identyczne rozwiązania zarówno o energii dodatniej, jak i ujemnej. Stąd funkcje (8)-(11) opisują nie tylko spoczywający elektron, ale także spoczywający pozyton.

Zatem nadal pozostawał niewyjaśniony problem interpretacji rozwiązań o ujemnej energii. Rozwiązał go w 1937 Kramers [11]. My w dalszej dyskusji oprzemy się na podręczniku [12]. Stąd podsumujmy.

1. Dirac wykazał, że elektron z ładunkiem -|e|, ale o ujemnej energii zachowuje się tak jak antyelektron o ładunku +|e| i dodatniej energii.

2. Pozyton został odkryty i rzeczywiście ma ten sam spin, tę samą masę spoczynkową co elektron, ale przeciwnego znaku ładunek elektryczny i powinien być opisywany przez równanie Diraca dla pozytonu.

Skoro elektron i pozyton mają tyle ze sobą wspólnego, to może da się otrzymać funkcję falową pozytonu o dodatniej energii bezpośrednio z funkcji falowej elektronu o ujemnej energii drogą jakiejś operacji algebraicznej zamiast rozwiązywać równanie Diraca dla pozytonu. Sformułujemy teraz problem matematycznie.

We wzorze (12) wyrażenie w nawiasie klamrowym, to operator Hamiltona dla równania Diraca w skrócie nazywany hamiltonianem Dirakowskim. Przyjmując za e ⇾ - e, otrzymamy hamiltonian Dirakowski dla elektronu, a e ⇾ e hamiltonian Dirakowski dla pozytonu.

Zastąpmy równanie (12) poniższymi dwoma

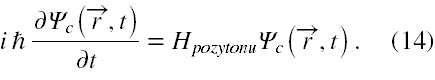
Przez H oznaczyliśmy hamiltonian Dirakowski, przez Ψ(r,t) funkcję falową elektronu, a przez Ψ_c(r,t) funkcję falową pozytonu.

Poddanie równania (13) pewnym operacjom algebraicznym takim, że w ich wyniku równanie (13) zamieni się dokładnie w równanie (14) pozwoli ustalić jakim operacjom też algebraicznym należy poddać funkcję falową dla elektronu, aby bezpośrednio z niej otrzymać funkcje falową dla pozytonu. I właśnie Kramers te operacje ustalił i nazwał łącznie sprzężeniem ładunkowym, które ma formę

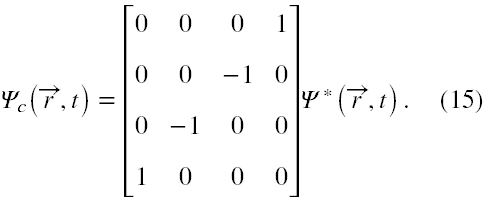
Nie będziemy sprawdzać poprawności wzoru (15) na funkcjach falowych (8)-(11), bo jest to zrobione w każdym podręczniku relatywistycznej mechaniki kwantowej, takim na przykład jak podręcznik Bjorkena-Drella, ale zrobimy to na funkcjach falowych elektronu i pozytonu w przedstawieniu standardowym dla potencjału elektrostatycznego typu bariery schodkowej, które otrzymałem w artykule Metody rozwiązywania równania Diraca - część 1. Otrzymane tam funkcje falowe elektronu i pozytonu istotnie różnią się.

Na podstawie tam znajdującego się wzoru (23) wypiszmy funkcję falową dla elektronu o energii ujemnej i spinie -1/2.

Po pierwsze za 'e' musimy podstawić '-e'. Dla uproszczenia przyjmiemy ruch elektronu tylko wzdłuż osi z, czyli p ⇾ (0,0,p_z). Zmienna E dla elektronu jest wtedy równa

E = eA₀ + √(p_z²c² + m²c⁴). (16)

Za C' musimy przyjąć

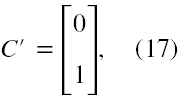
a funkcja falowa jest postaci

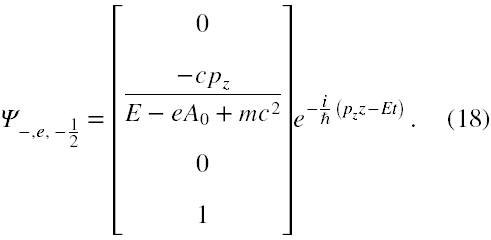
Na podstawie tam znajdującego się wzoru (20) wypiszmy funkcję falową dla pozytonu o energii dodatniej i spinie +1/2.

Teraz za 'e' musimy podstawić 'e'. Ponownie dla uproszczenia przyjmiemy ruch pozytonu tylko wzdłuż osi z, czyli p ⇾ (0,0,p_z). Zmienna E dla pozytonu jest wtedy równa

E = eA₀ + √(p_z²c² + m²c⁴). (19)

Za C musimy przyjąć

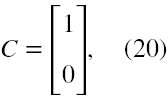
a funkcja falowa jest postaci

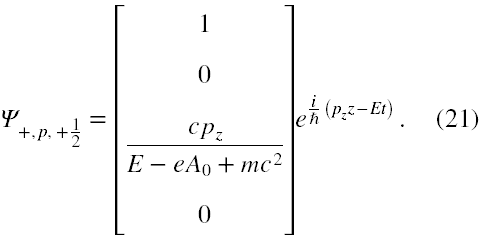
Zatem poddajmy funkcję falową (18) działaniu operacji (15). Najpierw wykonujemy sprzężenie zespolone w wykładniku funkcji eksponent, czyli zmieniamy znak przy 'i' na przeciwny, a następnie przemnażamy wektor-kolumnę przez kwadratową macierz (⁴). W wyniku tych operacji otrzymujemy dokładnie funkcję falową (21).

§5 Podsumowanie

W fizyce w zasadzie istnieje tylko jeden przypadek, gdy ciało fizyczne (cząstka kwantowa) może mieć ujemną energię całkowitą. Jest to przypadek, gdy ciało jest uwięzione w polu przyciągającego go centrum siły. Ujemność energii wskazuje, że ciało to bez źródła energii z zewnątrz samo się nie uwolni.

Istnieją rozwiązania o ujemnej energii relatywistycznych równań kwantowych takich jak równanie Diraca. Ich istnienie jednak nie oznacza, że cząstka lub antycząstka fizycznie posiada ujemną energię. W fizyce nie ma cząstek swobodnych o ujemnej energii.

W relatywistycznej mechanice kwantowej, a w szczególności dla równania Diraca istnieje swoista "nadreprezentacja" stanów, która przyjmuje następującą formę:

1. w równaniu dla elektronu rozwiązania o dodatniej energii opisują elektron, a o ujemnej reprezentują (⁵) pozyton,
2. w równaniu dla pozytonu rozwiązania o dodatniej energii opisują z kolei pozyton, a o ujemnej teraz reprezentują elektron.

Taka "nadreprezentacja" szczęśliwie umożliwia opis procesów kwantowych typu kreacja lub anihilacja pary pozyton-elektron, ponieważ niedopuszczalne jest użycie do obliczeń funkcji falowej z jednego równania jako opisującej elektron oraz innej z drugiego równania jako opisującej pozyton. Obie funkcje muszą być rozwiązaniami tego samego równania.

Można tylko skonstatować, że metody opisu świata fizycznego w mechanice kwantowej bardzo się różnią, szczególnie jeśli chodzi o intuicję od tychże w mechanice klasycznej.

Dopiero stworzenie Kwantowej Teorii Pola, na bazie relatywistycznej mechaniki kwantowej i przy pomocy operacji drugiej kwantyzacji, pozwoliło w pewnym sensie zapomnieć o rozwiązaniach o ujemnej energii. Ale to już zupełnie inna historia.

(¹) Masa zredukowana elektronu, to μ = mM/(m+M), gdzie m - to masa elektronu, a M - to masa jądra, patrz np. [4].

(²) Równanie to podobnie, jak i równanie Schrödingera opisuje zachowanie elektronu nie przy pomocy toru ruchu, ale za pomocą funkcji falowej, o której więcej napisałem w Co to jest funkcja falowa i po co jej używamy?

(³) Bronisław Średniawa w swoim podręczniku mechaniki kwantowej [8] tak to wyjaśnia.
Pakietem falowym nazywamy falę skoncentrowaną w przestrzeni, a więc falę opisaną przez funkcję falową mającą wartości różne od zera w skończonym obszarze przestrzeni, a poza tym obszarem znikającą.
  Obiekty kwantowe w stanie swobodnym, który odpowiada klasycznemu ruchowi jednostajnemu prostoliniowemu są opisane, niezależnie czy to wynika z równania Schrödingera czy Diraca, funkcją falową w postaci e^{-i(p·r - Et)/ℏ}. Taka funkcja ma kwadrat modułu |ψ(r,t)|² wszędzie równy 1. Z tego powodu takiemu obiektowi nie można przypisać w danej chwili czasu jakiegokolwiek konkretnego położenia. Aby obejść ten problem interpretacyjny mechaniki kwantowej wymyślono pakiet falowy.
  Problem interpretacyjny swobodnej funkcji falowej nie został tak naprawdę rozwiązany do dzisiaj, pojawiały się i nadal się pojawiają próby rozwiązania tej kwestii, między innymi także mojego autorstwa mająca tytuł "Czy cząstka kwantowa może poruszać się klasycznym torem ruchu?" - Część 1 oraz Część 2

(⁴) W wyniku mnożenia wektor kolumny przez kwadratową macierz otrzymujemy nowy wektor kolumnę o składowych według następującego schematu

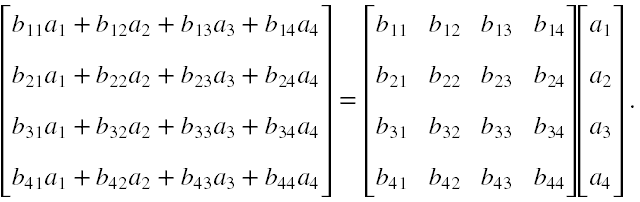
(⁵) Nieprzypadkowo użyłem słów "opisuje" i "reprezentuje" w taki sposób. "Opisuje" wiążemy z cząstką fizyczną, czyli stanem o dodatniej energii, bo cząstki fizyczne mają tylko energie dodatnie. Natomiast "reprezentuje" wiążemy z cząstką niefizyczną, czyli stanem o ujemnej energii, bo cząstka fizyczna nie może mieć ujemnej energii.

BIBLIOGRAFIA

[1] Kitty Ferguson, Krótka historia Stephena Hawkinga, Prószyński Media Sp. z o.o. Warszawa 2013.

[2] Stephen Hawking, Particle Creation by Black Holes, Commun. math. Phys. 43, 199—220 (1975) .

[3] H.A. Enge, M.R. Wehr, J.A. Richards, Wstęp do fizyki atomowej, §4-7 Model i teoria atomu Bohra, PWN, Warszawa 1983.

[4] Szczepan Szczeniowski, Fizyka doświadczalna, Część V Fizyka atomu, §21 Bohrowska teoria widma atomu wodoru, PWN, Warszawa 1974.

[5] Leonard Schiff, Mechanika Kwantowa, §16 Atom wodoru, PWN, Warszawa, 1977.

[6] Steven Weinberg, Teoria Pól Kwantowych,Tom I "Podstawy", strona 32 i dalsze, PWN, Warszawa 1999.

[7] Paul Dirac, A Theory of Electrons and Protons, Proc. R. Soc. A126, 360 (1930).

[8] Bronisław Średniawa, Mechanika Kwantowa, PWN, Warszawa, 1981.

[9] Paul Dirac, Quantized Singularities in the Electromagnetic Field, Proc. R. Soc. A133, 360 (1931).

[10] David L. Anderson, Odkrycie elektronu, rozdział 5, Dalszy rozwój fizyki elektronu, PWN, Warszawa, 1966.

[11] H.A. Kramers, The use of charge-conjugated wave-functions in the hole-theory of the electron, Proceedings Koninklijke Akademie van Wetenschappen 40, 814-823 (1937).

[12] J.D.Bjorken, S.D.Drell, Relatywistyczna teoria kwantów, Część I. Relatywistyczna mechanika kwantowa, §5.2, PWN, W-wa 1985.