W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 21

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: wtorek, 18 sierpień 2015 18:20

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 3.193 , Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Dwa działa znajdują się w odległości l = 300 m od siebie, lufy dział są ustawione w jednej płaszczyźnie pod jednakowymi kątami θ = 45° do poziomu (rys. 3.59). Z jakim opóźnieniem Δt w stosunku do pierwszego działa powinno wystrzelić drugie, aby pociski wystrzelone z prędkością początkową v₀ = 100 m/s zderzyły się w powietrzu?

pytanie uzupełniające, Janusz Szcząchor

Oblicz na jakiej wysokości i po jakim czasie od wystrzelenia drugiego pocisku nastąpi to zderzenie?

Rozwiązanie

Postanowiłem rozbudować to zadanie o dodatkowe pytanie, bo jego treść może stanowić ciekawy punkt wyjścia do analizy ruchów złożonych.

Powinieneś już wiedzieć, że rzut ukośny jest ruchem dwuwymiarowym, tj. leży w płaszczyźnie xy i jest on złożeniem dwóch niezależnych ruchów, wzdłuż osi x i osi y (na stronie poświęconej rzutowi ukośnemu możesz obejrzeć animację tego ruchu). Zastanówmy się co to znaczy z fizycznego punktu widzenia, że pociski zderzą się w powietrzu?

Odpowiedź może być tylko jedna. Dla pewnej chwili czasu t położenia obu pocisków muszą stać się identyczne i to co do współrzędnej x, jak i y (patrz rysunek nr 1 - Uwaga! To tylko szkic).

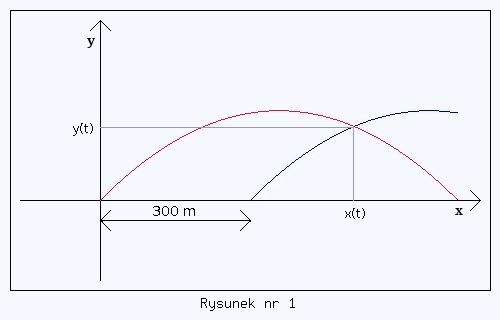
Aby obliczyć opóźnienie Δt z jakim trzeba wystrzelić drugi pocisk w stosunku do pierwszego, żeby pociski się zderzyły wystarczy wykonać obliczenia tylko dla osi x. Dlaczego?

Skoro ruchy pocisków wzdłuż osi x i y są niezależne, to oznacza, że warunków na zderzenie należy poszukiwać niezależnie dla każdej osi.

Zatem kiedy oba pociski będą miały to samo położenie na osi x ?

Zauważ, że oba pociski mają tę samą prędkość początkową. Stąd żaden z nich nie ma możliwości dogonienia drugiego. Dlatego z uwagi na różnicę położeń dział, aby pociski miały tę samą współrzędną x pocisk drugi musi być wystrzelony z takim opóźnieniem, aby w chwili jego wystrzelenia pierwszy pocisk znajdował się już w jego położeniu x. Tylko wtedy kontynuując lot oba pociski, mając różne współrzędne y, będą miały tę samą współrzędną x. Gdy prędkości początkowe obu pocisków są identyczne nie ma po prostu innej możliwości. Stąd współrzędna x pierwszego pocisku, to

x = v₀t cosθ, (1)

a drugiego

x^' = v₀t^'cosθ (2).

Uwzględniając to co powyżej wyjaśniłem, drugi pocisk znajdzie się w powietrzu później o Δt, które wiąże zmienne czasowe następująco

t^'= t - Δt. (3)

(Zauważ, że gdy t^' = 0, to t = Δt, lecz t^' nie może przyjmować wartości ujemnych!)

Tak więc równanie na warunek zderzenia obu pocisków dla współrzędnej x-owej,to

v₀tcosθ = l + v₀(t - Δt)cosθ. (4)

Przekształcenia są dość proste, skracamy stronami wyrazy z t, przenosimy wyraz z Δt na drugą stronę ze zmienionym znakiem, dzielimy stronami przez v₀cosθ i otrzymujemy rozwiązanie

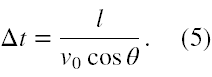
Mimo, że wynik zgadza się z odpowiedzią w zbiorze, to jednak jest to tylko warunek konieczny (jeśli chodzi o matematyczną poprawność) na zderzenie obu pocisków. Z tego jeszcze nie wynika, bez zbadania co się dzieje wzdłuż osi y, że do zderzenia w ogóle dojdzie. Dopiero ustalenie, że istnieje chwila czasu t > Δt, dla której położenia na osi y obu pocisków są identyczne oznacza, że do zderzenia faktycznie dojdzie. Stąd moje dodatkowe pytanie w treści zadania, to faktycznie pytanie o warunek dostateczny na zderzenie obu pocisków.

Warunek na identyczność tych współrzędnych to oczywiście

y(t) = y'(t - Δt), (6)

gdzie przez y i y' oznaczyłem odpowiednio współrzędne y-owe pierwszego pocisku oraz drugiego. Za oba y-i wstawiamy do (6) wzór na y dla rzutu ukośnego i otrzymujemy

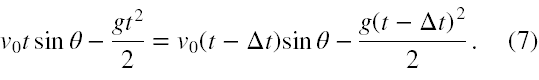
Redukujemy stronami wyrazy zawierające tylko t i celowo przenosimy wszystkie wyrazy z prawej strony na lewą ze zmienionymi znakami. Otrzymujemy wtedy równanie 8,

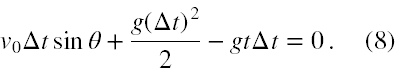
Zauważmy, że możemy wyłączyć Δt przed nawias. Otrzymamy wtedy dwa warunki na Δt. Pierwszy Δt = 0 jest oczywiście sprzeczny z tym otrzymanym we wzorze (5). Wprawdzie wtedy oba pociski też będą miały identyczne współrzędne y, lecz nigdy się nie zderzą. Zatem tą możliwość odrzucamy i z (8) obliczamy, że t jest równe

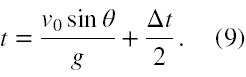
Niestety nie jest to jeszcze koniec analizy, ponieważ Δt nie jest daną, a wyliczoną wielkością, którą należałoby wstawić do (9). Zauważmy, że t musi być większe od Δt, a t' większe od 0. Zatem dalszą analizę możemy prowadzić w oparciu o t', bo warunek dla niego jest bardziej wyrazisty. Stąd po odjęciu od t wielkości Δt oraz podstawieniu za Δt wartości ze wzoru (5) otrzymujemy (po doprowadzeniu obu ułamków do wspólnego mianownika oraz skorzystaniu ze wzoru sin2θ = 2sinθcosθ)

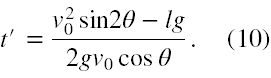
Otrzymaliśmy t' wyrażone tylko przez dane zadania. O tym, czy ułamek (10) jest większy od 0, decyduje znak licznika, ponieważ widzimy, że mianownik jest stale dodatni w granicach kąta podniesienia działa od 0° do 90° (cosθ dla kątów do 90° jest stale dodatni). Dla kąta θ = 45° otrzymujemy faktycznie warunek postaci

v₀² - gl > 0 .

Teraz możesz już sam sprawdzić, czy dane zadania spełniają warunek t' > 0. Jeśli tak (tutaj wartość v₀² - gl to około +7042 m²/s²), to aby wyliczyć wysokość y, na której nastąpi zderzenie pocisków należy podstawić do wzoru na y' wyliczoną w (10) wartość t'. Powinieneś otrzymać

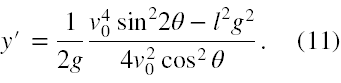
Podsumowanie

Dość często problem fizyczny dyskutowany w zadaniu wymaga dyskusji co do tego, czy otrzymany wynik spełnia założenia, przy których go otrzymaliśmy. W przypadku "zawodowej" fizyki pominięcie tego etapu jest nie do pomyślenia. Pamiętaj, że otrzymanie rozwiązania, które nie spełnia założeń wyprowadzenia oznacza, że:

1. zadanie nie ma rozwiązania, które dałoby się fizycznie zrealizować, albo
2. popełniliśmy błędy rachunkowe lub co gorsza błędnie zastosowaliśmy teorię fizyczną!