W jaki sposób nauczyć się rozwiązywać zadania z fizyki? - Część 22

Szczegóły

Kategoria: Zadania z fizyki

Opublikowano: wtorek, 18 sierpień 2015 19:20

Autor : Janusz Szcząchor

O mnie:

Nauczyciel w Centrum Nauki i Biznesu ŻAK w Łodzi oddział w Grudziądzu

zadanie nr 3.138 , Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Dwa ciała rzucono pionowo do góry tak, że jedno wzniosło się n = 4 razy wyżej niż drugie. Z jaką prędkością zostało rzucone ciało, które wzniosło się wyżej, jeżeli drugie ciało rzucono z prędkością v₁ = 8 m/s?  » Rozwiązanie

zadanie nr 3.142, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Ciało rzucono pionowo w dół. Prędkość przy upadku okazała się n = 5 razy większa od początkowej. Z jakiej wysokości rzucono ciało, jeśli czas spadania t = 3 s? Ile wynosiła prędkość początkowa? » Rozwiązanie

zadanie nr 3.148, Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

Oblicz prędkość początkową, z jaką rzucono ciało pionowo do góry, jeśli na wysokości h = 60 m znalazło się ono dwukrotnie w odstępie czasu t = 2 s ? » Rozwiązanie

Rozwiązanie

Ta część mojego poradnika została pomyślana jako zbiorowe repetytorium dla zagadnień swobodnego spadku ciał i rzutu pionowego. Podam tu rozwiązania 3 zadań, których teoria fizyczna jest typowa i charakterystyczna. Wszelkie tego typu zadania są jakąś wersją tychże i tych rozwiązań będzie można użyć jako wskazówek .

Na każde ciało znajdujące się na określonej wysokości nad Ziemią działa siła grawitacji. Jeżeli ta wysokość nie jest zbyt duża, to możemy zakładać, że pole grawitacji Ziemi jest jednorodne, czyli wartość przyspieszenia ziemskiego z jakim się to ciało porusza jest stała i wynosi g.

Stąd ruch każdego ciała w pobliżu Ziemi przy tym założeniu należy traktować jako ruch ze stałym przyspieszeniem. Są zatem do rozpatrzenia dwa przypadki.

Typ 1) Gdy ciało spada pionowo w dół, z ewentualnie nadaną mu prędkością początkową do dołu, to mamy do czynienia z ruchem jednostajnie przyspieszonym bez lub z prędkością początkową.

Typ 2) Gdy ciało zostało rzucone pionowo do góry, to mamy ruch jednostajnie opóźniony. Taki ruch zawsze jest z prędkością początkową. Patrz rysunek nr 1.

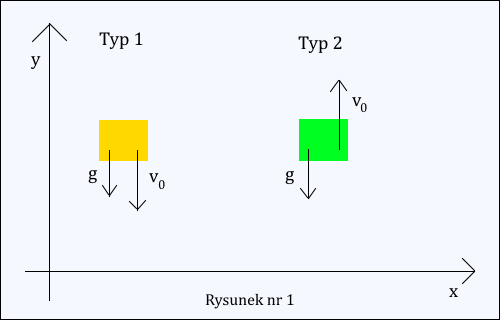
Przechodzimy do zadań. Na określoną tutaj nomenklaturę będę się powoływał w treści rozwiązań.

§1 Rozwiązanie zadania nr 3.138 ¹

Ruch obu ciał jest typu 2. Wzór na drogę w tym ruchu jest dany jako

h = v₀t - gt²/2, (1)

przy założeniu, że h₀ = 0, tzn. ciało wyrzucono z powierzchni Ziemi. Oczywiście, aby obliczyć h musimy znać czas lotu danego ciała.

Czas lotu ciała, o który chodzi w tym zadaniu, to czas jaki upłynął od chwili jego wyrzucenia w górę do chwili osiągnięcia przez nie maksymalnej wysokości. Ma to miejsce w punkcie zwrotu, gdy ciało przestaje się wznosić i zaczyna opadać. Przekładając to na język prędkości oznacza, że potrzebne jest wyznaczenie chwili czasu, dla której wartość prędkości jest równa 0. Wyznaczymy ten czas z równania (prędkość w ruchu jednostajnie opóźnionym przyrównana do 0)

v = v₀ - gt = 0 . (2)

Czyli po prostych przekształceniach mamy

t = v₀/g . (3)

Żeby rozwiązać nasze zadanie wprowadźmy oznaczenia sygnowane 1 dla ciała o nieznanej prędkości, a 2 dla ciała o prędkości początkowej 8 m/s. Zmieniłem tu oznaczenia w stosunku do treści zadania, bo jego autorzy są niekonsekwentni w logicznym łączeniu treści zadania i stosowanych w nim oznaczeń. Zatem równanie (1) dla ciała pierwszego przyjmie postać

h₁ = v₁t₁ - gt₁²/2. (4)

Po obliczeniu czasu wznoszenia się tego ciała zgodnie ze wzorem (3), czyli

t₁ = v₁/g, (5)

i podstawieniu tego do (4) mamy

h₁ = v₁²/g - gv₁²/2g² = v₁²/2g . (6)

Zatem dla ciała drugiego jest h₂ = v₂²/2g . Ponieważ zgodnie z treścią zadania ciało pierwsze wzniosło się n = 4 razy wyżej niż drugie, zatem możemy to opisać następującą równością

h₁ = nh₂ , (7)

czyli

v₁²/2g = nv₂²/2g. (8)

Skracając stronami mianowniki i również stronami wyciągając pierwiastek mamy, że

v₁ = (√n)v₂ . (9)

§1 Rozwiązanie zadania nr 3.142 ²

Teraz ruch ciała jest typu 1. Ponieważ w treści zadania mamy pewne dane na temat prędkości ciała i czasu jego lotu, więc wypiszmy wzór na prędkość ciała dostrzegając, że jego ruch to ruch jednostajnie przyspieszony z prędkością początkową, czyli

v(t) = v₀ + gt . (10)

Ponieważ mamy podane, że prędkość końcowa ciała była 5 razy większa od początkowej, więc możemy policzyć ile wynosiła prędkość początkowa ciała. W tym celu za v(t) w (10) podstawmy nv₀ i mamy

nv₀ = v₀ + gt . (11)

Przenosimy v₀ ze zmienionym znakiem na lewą stronę, wyciągamy v₀ przed nawias, dzielimy stronami (11) przez (n-1) i otrzymujemy, że prędkość początkowa ciała jest równa

v₀ = gt/(n-1) , (12)

co jest odpowiedzią na drugie z pytań zadania.

Aby obliczyć wysokość z jakiej rzucono ciało wypiszmy równanie na drogę w tym ruchu. Zauważmy, że wysokość z jakiej ciało zostało rzucone, to jego droga początkowa (i jednocześnie poszukiwana przez Nas wielkość), ruch jest z prędkością początkową v₀ oraz a = g, czyli

h(t) = h₀(t) - v₀t - gt²/2 . (13)

Droga początkowa została oznaczona jako zależna od t, ponieważ zgodnie z warunkami zadania im dłuższy czas spadania ciała, tym większa wysokość, z kórej spadło ciało.

Zgodnie z treścią zadania ciało po czasie t osiągnęło powierzchnię Ziemi, czyli h(t) = 0. Zatem ze wzoru (13) otrzymujemy

h₀(t) = v₀t + gt²/2 . (13a)

Za v₀ podstawmy do (13a), to co wyliczyliśmy w (12) i mamy

h₀(t) = gt²/(n-1) + gt²/2 . (14)

Musimy teraz oba ułamki w (14) sprowadzić do wspólnego mianownika, który ma postać 2(n-1). Przekształcając wzory, mamy kolejno aż do otrzymania odpowiedzi na pierwsze z pytań zadania

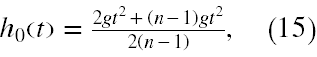
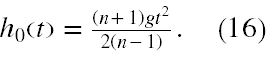
§3 Rozwiązanie zadania nr 3.148 ³

Choć opisany w zadaniu ruch dotyczy jednego ciała, to jednak jeśli chodzi o równania ruchu, to mamy do czynienia z dwoma fizycznie różnymi ruchami. Są tutaj połączone oba przypadki ruchów z poprzednich zadań. Ustalmy zatem postacie obu równań ruchu.

Gdy nasze ciało porusza się w górę, to wykonuje ruch jednostajnie opóźniony z prędkością początkową (którą musimy obliczyć), czyli jego droga jest dana jako (przy założeniu, że droga początkowa jest równa 0)

h(t) = v₀t - gt²/2, (17)

gdzie v₀ - nieznana prędkość początkowa. Oczywistym jest, że dla pewnej chwili czasu, oznaczmy ją jako t₁, prędkość ciała spadnie do zera i ten ruch ciała zakończy się. Wówczas

h(t₁) = v₀t₁ - g(t₁)²/2 . (18)

Jeśli chodzi o ruch ciała w dół, to zauważmy, że h(t₁) jest jego drogą początkową. Zatem jego równanie ruchu przyjmuje postać (19), gdzie dla odróżnienia ruchów ciała zmienną czasową oznaczyłem jako t'

h'(t') = h(t₁) - g(t')²/2 , (19)

a przez h'(t') oznaczyłem bieżące położenie ciała w tym ruchu.

Powstaje teraz pytanie jak wykorzystać dane zadania do obliczenia prędkości początkowej ciała?

Po pierwsze, dla naszych obliczeń załóżmy chwilowo, że znamy wartość v₀. Wtedy korzystając ze wzoru (3) z rozwiązania zadania 3.138 możemy napisać, że

t₁ = v₀/g , (20)

a tym samym analogicznie do wzoru (6) z tegoż zadania możemy obliczyć z (18), że

h(t₁) = v₀²/2g . (21)

Zatem tak obliczone h(t₁) możemy wstawić do (19) i pozbyć się tej zmiennej pośredniej, zostanie to użyte we wzorze (29).

Celem usunięcia wątpliwości podkreślam, że podczas wznoszenia się i podczas opadania, ze względu na zmianę postaci równania opisującego ruch ciała, występujące w tychże równaniach zmienne czasowe to różne zmienne i dlatego nie można w nich zastosować do obliczeń identycznego symbolu (aby nie dochodziło do omyłek).

Stąd dany w zadaniu odstęp czasu 2s faktycznie składa się z dwóch przedziałów czasu. Dla odróżnienia od zmiennych czasowych oznaczmy go chwilowo jako Δt.

Zatem odstęp ten składa się z przedziału, nazwijmy pierwszego, który trwał od chwili osiągnięcia przez ciało wysokości 60m po raz pierwszy, oznaczmy te chwilę jako t₀, do momentu osiągnięcia przez nie maksymalnej wysokości w chwili oznaczonej już uprzednio jako t₁. Oraz drugiego, który trwał od chwili rozpoczęcia przez ciało spadku do chwili osiągnięcia przez nie ponownie wysokości 60m, którą oznaczymy jako t₂. Ponieważ można przyjąć, że początek spadania zaczął się w chwili t' = 0s, więc chwilę t₂ można użyć jako miary tego drugiego przedziału.

Stąd mamy następujący bilans czasu dla łącznego ruchu ciała w formie

Δt = t₁ - t₀ + t₂ = 2s . (22)

Ponieważ już wyraziliśmy t₁ jako funkcję v₀, więc możemy podobnie wyznaczyć t₀ i t₂ jako funkcje tejże. Zrobimy to na pdst. równań ruchu (17) i (19).

A zatem dla chwili czasu t = t₀ równanie (17) przyjmuje postać zgodnie z danymi zadania w formie

h = v₀t₀ - g(t₀)²/2 , (23)

gdzie h, to dana zadania równa 60 m. Wyrażenia z prawej strony (23) przenosimy na lewą ze zmienionymi znakami i otrzymujemy równanie kwadratowe na t₀

g(t₀)²/2 - v₀t₀ + h = 0 . (24)

Współczynniki trójmianu kwadratowego są równe (tutaj wyjątkowo pogrubienie nie oznacza wektorów)

a = g/2 , b = -v₀, c = h. (25)

Zatem

Δ = b² - 4ac = (v₀)² - 2gh . (26)

I stąd dalej (wzór na rozwiązanie równania kwadratowego - patrz "W jaki sposób nauczyć się rozwiązywać zadania z fizyki?- Część 7")

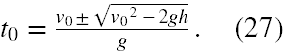
Musimy przedyskutować znak ± . Przedział czasu t₁ - t₀ musi być oczywiście dodatni (t₁ dane jest wzorem (20)), czyli

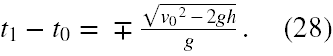
Widać, że w (28) w grę wchodzi wyłącznie rozwiązanie ze znakiem " + ".

Jeśli chodzi o chwilę czasu t₂, to z (19) i (21) mamy (gdzie h, to dana zadania równa 60 m)

h = v₀²/2g - g(t₂)²/2 . (29)

Z (29) możemy wyliczyć, że

g(t₂)²/2 = v₀²/2g - h. (30)

Doprowadźmy prawa stronę (30) do wspólnego mianownika 2g, a następnie pomnóżmy to wyrażenie stronami przez 2/g , a w końcu wyciągnijmy stronami pierwiastek kwadratowy i otrzymujemy

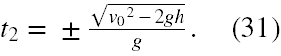
Oczywiście w grę ponownie wchodzi tylko rozwiązanie z " + " i ostatecznie wstawiając otrzymane wyniki (28) i (31) do (22) otrzymujemy, że

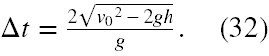
Teraz możemy już wyliczyć v₀ . W tym celu podnosimy (32) stronami do kwadratu, mnożymy stronami przez g², rozwijamy nawias po prawej stronie i przenosimy wyraz z h na drugą stronę ze zmienionym znakiem, obracamy stronami równanie, dzielimy stronami przez 4, wyciągamy stronami pierwiastek kwadratowy, wybieramy wynik z " + " i mamy rozwiązanie

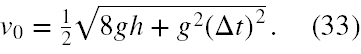
W odpowiedzi do tego zadania zawartej w wydaniu zbioru z roku 1976 jest błąd, natomiast w wydaniu z roku 1992 jest prawidłowa odpowiedź, zadanie to umieszczono tam pod numerem 210. Poprawiono także oznaczenie danych w zadaniu zastępując symbol t oczywistym Δt.