O poszukiwaniu stanów stacjonarnych w mechanice kwantowej

Szczegóły

Kategoria: Publikacje naukowe

Opublikowano:środa, 6 styczeń 2021 21:30

Autor : Janusz Szcząchor

On the search for stationary states in quantum mechanics

Abstract: Notion of the stationary quantum state is recalled. The classical way of finding stationary states for the Schrödinger equation is analysed. Attention is paid to the difference between the notion of physical stationary state and mathematical notion of function with separated variables. The mathematical basis of some general method for solving the Dirac equation is presented. The problem of finding stationary solutions for the case of the Dirac equation is analysed. A conclusion appears that there are no stationary states for the Dirac equation in a homogeneous electric field. Results of our paper [1] are confronted with some papers of other authors dealing with the problem of a homogeneous or constant electric field.

1. Wstęp

Przesłaniem tej pracy jest rzucenie szerszego światła na cele i motywację powstania naszej pracy [1] ze wskazaniem na istotność poruszonego w niej problemu znajdowania stanów stacjonarnych dla równań kwantowych. Można ją potraktować jako pewnego rodzaju suplement do tamtej pracy.

Wśród prac z relatywistycznej mechaniki kwantowej odnaleźliśmy kilka, po lekturze których można odnieść wrażenie, że fizycy tak się przyzwyczaili do istnienia stanów stacjonarnych, że są przekonani, iż w dowolnym polu elektromagnetycznym istnieją stany stacjonarne. Niestety, nie jest to prawdą.

Być może można to wytłumaczyć faktem, że znaczna część badań doświadczalnych fizyki kwantowej dotyczy atomów, których stany to rozwiązania równań kwantowych dla pola Kulombowskiego, o którym z doświadczenia wiemy, że ma stany stacjonarne.

Jednak matematyczny dowód tego faktu w przypadku równania Diraca dla atomu wodoru nie jest taki prosty, a i w podręcznikach mechaniki kwantowej je prezentujących i tak się pomija niektóre matematyczne szczegóły, które są rachunkowo szczególnie uciążliwe.

Co więcej niektóre z tych podręczników przedstawiają w dość pobieżny sposób samą metodę znajdowania stanów stacjonarnych co może wywoływać wśród fizyków odczucie banalności tego zagadnienia.

2. Co to są stany stacjonarne?

Historia odkrycia stanów stacjonarnych zaczyna się w końcu XIX wieku, przypomnimy tu podstawowe fakty za [2].

Dzięki intensywnemu rozwojowi spektroskopii z użyciem spektrometrów pryzmatycznych i siatkowych zaobserwowano, że światło emitowane przez pierwiastki będące w fazie gazowej daje nieciągłe widmo liniowe.

Zgodnie z modelem atomu Thomsona elektrony mogły emitować światło po wytrąceniu z położenia równowagi, którego częstość powinna być równa częstości drgań elektronu lub jej harmonicznych. Zagadkowe było to, że atomy nie emitowały linii o częstościach będących harmonicznymi częstości podstawowej.

Odkrycie jądra atomowego przez Rutherforda nasunęło hipotezę, że elektrony poruszają się po orbitach kołowych wokół jądra, a siła Kulombowskiego przyciągania spełnia rolę siły dośrodkowej. Jednak zgodnie z elektrodynamiką klasyczną elektron poruszający się z przyspieszeniem a, w tym również dośrodkowym jest źródłem promieniowania o mocy P = e²a²/6πε₀c³ W. Tym samym elektron w ruchu orbitalnym powinien tracić energię i ruchem spiralnym po 10^-8 s, spaść na jądro.

Jak wynika z [3][4][5] Bohr wkrótce po pojawieniu się modelu atomu Rutherforda postanowił go udoskonalić i skutecznie wyjaśnić widmo atomu wodoru pogrupowane w serie Balmera, Lymana, Paschena i inne.

W tym celu wyszedł on od wyrażenia na energię elektronu na dowolnej kołowej orbicie planetarnej dla atomu wodoru i różnicę energii na dwóch różnych takich orbitach próbował dopasować do energii fotonów doświadczalnie obserwowanych linii widmowych.

Udało się to przy przyjęciu założenia, że tylko niektóre orbity są dozwolone. Energia całkowita elektronu na takiej orbicie jest oczywiście ściśle określona i stała w czasie. Orbity te nazwano stacjonarnymi.

Gdy Bohr policzył orbitalny moment pędu na takich orbitach to okazało się, że jest on równy wielokrotności stałej Plancka. Z uwagi na jego prostotę można było się pokusić o podniesienie znaczenia tego faktu do rangi postulatu.

Jednak jak wskazuje autor [6], wielu fizyków wówczas uważało taki postulat za zbyt niezrozumiały, aby można go było traktować wprost jako fundament kwantowej teorii. Byli oni przekonani o konieczności stworzenia nowej ogólniejszej teorii, która zastąpiłaby mechanikę klasyczną w opisie atomów.

W toku poszukiwań takiej teorii wykrystalizowały się dwa kierunki badań. Pierwszy wskazany przez de’Broglie’a zyskał miano mechaniki falowej, a drugi wskazany przez Heisenberga miano mechaniki macierzowej. Born ukuł nazwę nowej teorii jako mechanika kwantowa, a niedługo potem Schrödinger wykazał równoważność obu podejść do problemu.

W toku powstawania mechaniki kwantowej stało się jasne, że opis materii nie może polegać tylko na przypisaniu cząstce skalarnych wartości masy, ładunku elektrycznego, energii czy wielkości wektorowych pędu, momentu pędu.

Okazało się, że takiemu obiektowi fizycznemu musi zostać przypisana funkcja falowa opisująca własności materii w czasowoprzestrzennym teatrze zdarzeń, a wielkości fizyczne są reprezentowane przez operatory, które dopiero w działaniu na funkcję falową dają wartości tych wielkości fizycznych.

Funkcja falowa zawiera w sobie informację nie tylko o wartościach wielkości fizycznych charakterystycznych dla danej cząstki, ale także informację o kierunku przebiegu zjawisk fizycznych jakim dana cząstka podlega.

Stąd wynikła potrzeba emocjonalnego podkreślenia (tak przynajmniej My to odbieramy), że funkcja falowa to nie jakaś funkcja matematyczna, ale wielkość fizyczna szczególnej kategorii i dlatego obdarzono ją alternatywną nazwą stanu cząstki kwantowej.

Tym samym dochodzi do podziału stanów cząstki na stacjonarne, w których cząstka ma stałą w czasie wartość energii i nie oddziałuje z kwantami pól oddziaływań oraz na wszystkie pozostałe, w których następuje jej interakcja z tymi kwantami, czyli stany niestacjonarne.

Jest oczywiste, że Bohrowskim orbitom stacjonarnym w mechanice kwantowej powinny odpowiadać stany, funkcje falowe stacjonarne.

3. Poszukiwanie stanów stacjonarnych w przypadku nierelatywistycznym

Jeżeli ograniczymy się do oddziaływań elektromagnetycznych, to w tym przypadku opis cząstki kwantowej sprowadza się do rozwiązania równania Schrödingera, w wyniku czego otrzymujemy przeliczalny lub nieprzeliczalny zbiór rozwiązań, z których każde jest pojedynczą (skalarną) na ogół zespoloną funkcją matematyczną (¹) zależną od zmiennych x, y, z, t.

Równanie Schrödingera w postaci ogólnej to

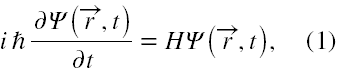
gdzie H operator Hamiltona układu, który na ogół zawiera człon opisujący jego oddziaływanie z polem elektromagnetycznym.

O tym czy dany stan Ψ jest stacjonarny (²), czy nie decyduje sposób zachowania się funkcji falowej względem operatora energii

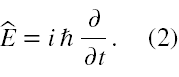
Jeżeli działając tym operatorem na tę funkcję otrzymamy równanie na wartości własne postaci

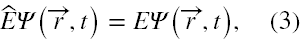
gdzie E jest liczbą rzeczywistą, to dany stan jest stacjonarnym (³) o wartości energii E.

Standardowe podręczniki mechaniki kwantowej [7-20] informują, że w takim przypadku funkcja falowa, w części zależnej od czasu powinna mieć formę

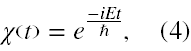
a cały stan stacjonarny ma postać

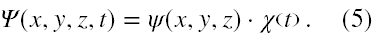
Aby miało sens poszukiwanie stanów stacjonarnych w danym zagadnieniu fizycznym operator H musi mieć postać sumy

H = H₀ + H_I, (6)

gdzie składnik H₀ nie zawiera czasu, a składnik H_I opisujący oddziaływaniem układu z polem jest na tyle mały, że oddziaływanie to można potraktować jako zaburzenie układu stacjonarnego (⁴). Oznacza to, że równanie

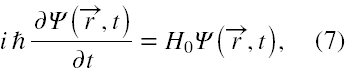
powinno w wyniku rozwiązania dać stany postaci (5), jeżeli posiada rozwiązania stacjonarne.

Wydawałoby się więc, że teraz wystarczy wstawić (5) do (7) i rozwiązać równanie. Niestety, takie nieostrożne postępowanie może prowadzić do błędnych rozwiązań.

Szereg podręczników mechaniki kwantowej [7-9,16,19-20] przedstawia pełną procedurę jak zbadać, czy rozwiązanie równania (7) może być zapisane w formie (5), ale są i takie [10-15,17-18], które podchodzą do tego problemu cokolwiek pobieżnie.

Jak taka procedura ma wyglądać pokażemy na przykładzie dwuwymiarowego równania falowego. Fragment ten został oparty na klasycznym podręczniku analizy matematycznej [23].

Dwuwymiarowe równanie falowe ma postać

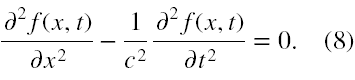
Pomińmy tu, jako mniej istotne dla ilustracji problemu, zagadnienie warunków brzegowych równania. Aby ustalić, czy (8) może posiadać rozwiązania stacjonarne postaci (5), musimy najpierw zbadać czy są dopuszczalne w tym równaniu rozwiązania o rozdzielonych zmiennych t i x.

W tym celu (⁵) przedstawmy rozwiązanie próbne jako

f(x,t) = T(t)·X(x),

które wstawiamy do (8). W wyniku obliczeń otrzymujemy kolejno

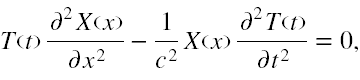
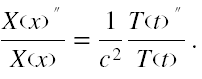
Po lewej stronie jest funkcja zależna tylko od zmiennej x, a po prawej tylko od t. Zatem równość jest możliwa tylko wtedy, gdy zarówno lewa strona, jak i prawa nie zależą ani od x, ani od t, czyli są równe jednej i tej samej stałej. Oznaczmy ją jako -k² i mamy

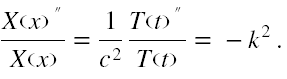
Stąd otrzymujemy do rozwiązania dwa niezależne równania

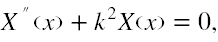
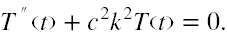
Dopiero teraz rozwiązanie drugiego z tych równań pozwoli odpowiedzieć na pytanie, czy równanie (8) ma rozwiązania stacjonarne. Procedura ta jest ogólna i dotyczy dowolnych równań różniczkowych cząstkowych.

Jako ilustrację z zakresu nierelatywistycznej mechaniki kwantowej proponujemy rozwiązanie równania Schrödingera dla przypadku ruchu elektronu w jednorodnym polu elektrycznym przedstawione w [11].

Przyjmując kierunek pola wzdłuż osi x, oznaczając jako F = eE siłę działającą na cząstkę w polu elektrycznym o natężeniu E, gdzie ładunek cząstki to e (⁶) mamy, że energia potencjalna cząstki w tym polu to

U = -Fx + const.

Za autorami [11] przyjmujemy const = 0, aby dla x = 0 było U = 0. Zatem niestacjonarne równanie Schrödingera w tym polu ma ostateczną formę

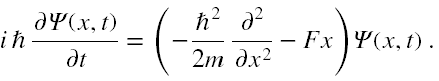
Podstawmy więc Ψ(x,t) = T(t)∙X(x) i zbadajmy, czy w tym przypadku jest dopuszczalne rozwiązanie o rozdzielonych zmiennych (⁷). Prowadząc standardowe rachunki otrzymujemy, że

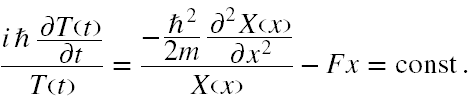
Przyjmując const = ε, stałą o wymiarze energii, czyli energię stanu stacjonarnego (⁸), można już przystąpić do rozwiązywania niezależnych równań na T(t) i X(x). Za autorami [11] podajemy, że rozwiązaniem o dowolnej energii ε jest stan

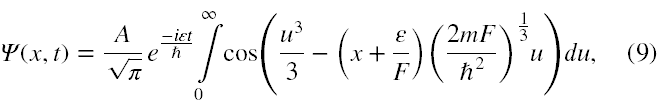
gdzie A to pewna stała.

4. Poszukiwanie stanów stacjonarnych w przypadku relatywistycznym

Ponownie ograniczymy się do oddziaływań elektromagnetycznych, ale i także cząstek o spinie ½. Zagadnienie to opisuje równanie Diraca, które można zapisać w postaci

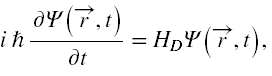
gdzie H_D to macierz operatorów różniczkowych zwyczajowo zwana hamiltonianem Diraca. Jest to zapis często stosowany, aby uwypuklić podobieństwo tego równania do równania Schrödingera.

Jednak metoda poszukiwania stanów stacjonarnych w tym przypadku nie może być kalką takiego postępowania dla równania Schrödingera, albowiem równanie Diraca jest układem czterech równań różniczkowych cząstkowych pierwszego rzędu na funkcję falową będącą układem (wektorem zwanym bispinorem) czterech matematycznych zespolonych funkcji skalarnych.

Typowe uniwersyteckie studia dla fizyków w ogóle nie uczą jak rozwiązywać takie zagadnienia matematyczne. Co więcej współczesne podręczniki traktujące o równaniach różniczkowych cząstkowych, np. [24] raczej skupiają się na dowodach istnienia słabych lub silnych rozwiązań takich zagadnień.

Dlatego najlepszym rozwiązaniem jest zajrzenie do starych podręczników analizy matematycznej szczegółowo tłumaczących te zagadnienia rozwiązane jeszcze w XIX wieku. Akurat w naszym ojczystym języku dysponowaliśmy trzema doskonałymi pozycjami [21,22,23].

Po ich lekturze można dojść do wniosku, że najbardziej obiecującym kierunkiem postępowania jest wykorzystanie metody mówiącej, że całkowanie układu równań różniczkowych można spróbować sprowadzić do całkowania jednego równania różniczkowego wyższego rzędu.

Aby było wszystko jasne szczegółowo przedstawimy rozumowanie (⁹) zawarte w [23]. Dla przykładu rozpatrzmy przypadek układu trzech równań różniczkowych rzędu pierwszego (dla prostoty zwyczajnych), rozwiązanego względem pochodnych

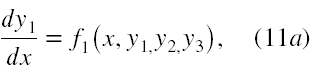
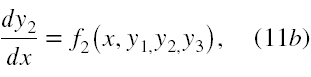
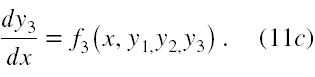
Załóżmy, że (11a) istotnie zawiera y₂ i potrafimy je rozwiązać względem y₂. Zatem mamy

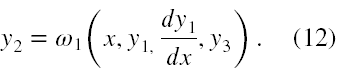
Obliczając formalnie pochodną funkcji złożonej y₂ (12) i podstawiając to za lewą stronę (11b) oraz podstawiając (12) do prawej strony (11b) otrzymujemy nową wersję równania (11b)

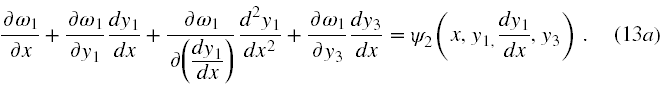
Z kolei podstawiając (12) do (11c) mamy nową wersję i tego równania

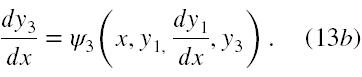
W końcu podstawiając ψ₃ z (13b) do (13a) w miejsce dy₃/dx i rozwiązując (13a) względem d²y₁/dx² oraz oznaczając ψ₃ jako χ₃ otrzymujemy układ równań (14) równoważny wyjściowemu układowi (10).

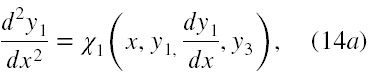
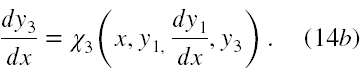
Ponownie zakładając, że potrafimy rozwiązać równanie (14a) względem y₃ możemy z niego otrzymać, że

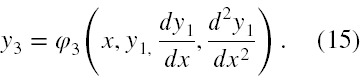
Obliczając formalnie pochodną z y₃ jako funkcji złożonej (15) oraz podstawiając to za lewą stronę (14b) oraz wstawiając (15) do prawej strony (14b) otrzymujemy nową wersję równania (14b)

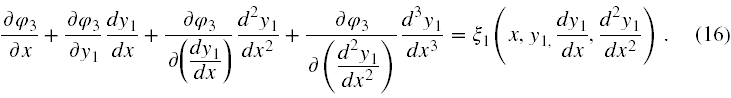
Równanie (16) jest po prostu równaniem różniczkowym trzeciego rzędu na y₁

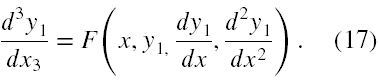
Jeżeli potrafimy scałkować (17), to jego formalne rozwiązanie będzie miało postać

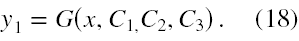
Podstawiając (18) do (15) otrzymujemy y₃ bez żadnych całkowań oraz podstawiając je do (12) wraz (15) otrzymujemy y₂ również bez żadnych całkowań.

W przypadku równania Diraca mamy zatem perspektywę zastąpienia układu czterech równań równaniem czwartego rzędu co nie jest przyjemną wiadomością, ale trzeba pamiętać, że są to równania różniczkowe cząstkowe na funkcje zespolone.

Na szczęście istnieje przedstawienie macierzy Diraca zwane spinorowym [15], które pozwala obniżyć problem o dwa rzędy. Ponownie zajmiemy się zagadnieniem jednorodnego pola elektrycznego, którego źródłem jest tylko potencjał skalarny A₀. Przy takich założeniach wyjściowych równanie Diraca można zapisać w formie [1]

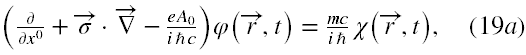
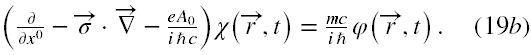
gdzie φ(r,t) to dwie górne składowe, a χ(r,t) to dwie dolne składowe bispinorowej funkcji falowej, x⁰= ct.

Skoro na prawych stronach (19) spinory są wymnożone przez liczby, więc przy pomocy opisanej wyżej metody podwyższania rzędu równań możemy je zastąpić nowym układem w postaci

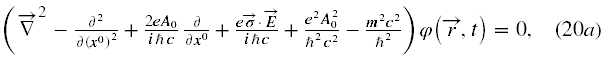
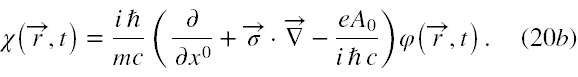
Rzeczywiście mamy równanie różniczkowe (cząstkowe) drugiego rzędu na górny bispinor, a dolny bispinor otrzymujemy z górnego tylko przez różniczkowanie. Jednak macierze Pauliego w (20a) mieszają obie składowe górnego bispinora ze sobą. Aby ostatecznie uniknąć perspektywy rozwiązywania równania czwartego rzędu skierowujemy pole elektryczne wzdłuż osi z, czyli przyjmujemy

A₀ = εz, E = -εk

gdzie ε to stała dodatnia, gdyż tylko macierz σ_z jest diagonalna.

Ponieważ teraz wzdłuż osi x i y cząstka odbywa ruch swobodny, więc możemy problem jeszcze uprościć przyjmując, że składowe pędu cząstki wzdłuż tych osi są równe zero. Pozbywamy się wtedy z (20) różniczkowania po tych zmiennych, a spinory stają się funkcjami tylko zmiennych z i x⁰. Ostatecznie otrzymujemy równoważny wyjściowemu równaniu Diraca (19) układ równań (¹⁰) w formie

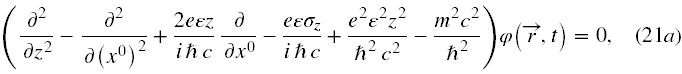
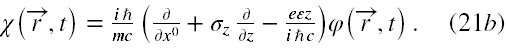
W ten sposób rozwiązywanie równania Diraca w jednorodnym polu elektrycznym, którego źródłem jest potencjał skalarny sprowadza się do rozwiązywania jednego równania różniczkowego drugiego rzędu czy to na φ¹ (a χ¹ dostajemy poprzez różniczkowanie tej pierwszej), czy na φ² (a χ² uzyskujemy podobnie jak χ¹). Nie powinno ulegać wątpliwości, że składowe φ¹ i χ¹ są niezależne od φ² i χ², a każde z nich opisują niezależne stany polaryzacyjne cząstki.

Zanim będziemy badać, czy równanie (21) ma rozwiązania stacjonarne zastanówmy się co oznacza pojęcie stacjonarności dla równania Diraca?

Skoro stan kwantowy jest opisany bispinorem, zatem teraz każda jego składowa powinna zawierać czynnik postaci (4) przynależny do tej samej wartości energii E. Zauważmy, że opisana powyżej metoda rozwiązywania równania Diraca ułatwia nam poszukiwanie takich rozwiązań.

Załóżmy, że składowa φ^k (k =1,2) ma już postać (5). Aby otrzymać χ^k należy zgodnie z (21b) podziałać na φ^k operatorami ∂/∂x⁰ i ∂/∂z, które w żaden sposób nie mogą wynieść zależności od czasu poza eksponent e^-iEt/ℏ. Zatem wtedy χ^k również będzie postaci (5), choć zależność od zmiennych przestrzennych może być inna. Widzimy stąd, że aby ustalić, czy układ równań (21) ma rozwiązania stacjonarne wystarczy sprawdzić czy ma je równanie (21a).

Zbadajmy teraz czy rozwiązania φ^k (k =1,2) mogą być stacjonarne. Ponownie, w tym celu najpierw musimy zbadać, czy da się w nich rozseparować zmienne z i t.

Podstawiając φ^k(z,t) = Z^k(z)∙T^k(t) (k = 1,2) do (21a) oraz dokonując standardowych przekształceń otrzymujemy

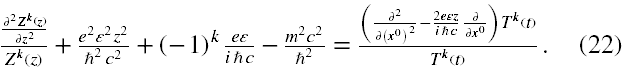
Z powodu obecności po prawej stronie (22) członu

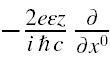
wiążącego ze sobą zmienne t i z nie jest możliwa separacja tych zmiennych w równaniu (21a). Zatem równanie Diraca w jednorodnym polu elektrycznym nie posiada rozwiązań stacjonarnych. Stąd nie pozostaje nic innego jak znaleźć rozwiązania niestacjonarne.

5. Podsumowanie

Z wielu powodów, mniej więcej od lat 40-tych XX wieku rozwój mechaniki kwantowej w sferze zagadnień relatywistycznych następował głównie na kierunku kwantowej teorii pola, gdzie królują metody perturbacyjno-propagatorowe oparte na diagramach Feynmana. Stąd obecnie w zasadzie nie uczy się studentów fizyki systematycznych metod rozwiązywania równania Diraca.

Nieliczne opisy takich metod, które są zawarte w podręcznikach akademickich, na przykład w [15] nie satysfakcjonowały nas między innymi dlatego, że zostały podane w zasadzie bez dowodu. Stąd postanowiliśmy opracować własną taką metodę opartą na czytelnym matematycznym uzasadnieniu.

Owocem tych działań jest metoda przedstawiona w poprzednim paragrafie. Pierwszym zagadnieniem, do rozwiązania którego jej użyliśmy jest przypadek jednorodnego pola elektrycznego przedstawiony w pracy [1]. Podczas powstawania tej pracy nie znaliśmy innych prób rozwiązania tego zagadnienia. Dopiero po otrzymaniu jej głównych wyników postanowiliśmy sprawdzić, czy były już takie próby w przeszłości. Okazało się, że było ich kilka, a oto efekt porównania wyników naszej pracy z wynikami tamtych prac.

Fritz Sauter był pierwszym, który usiłował rozwiązać równanie Diraca dla przypadku jednorodnego pola elektrycznego [25]. Potencjałowi skalarnemu dla tego pola nadał formę

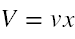
i szukając rozwiązania zastosował następujące podstawienie

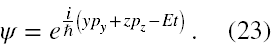
Kolejnym był Milton Plesset [26]. Rozważył on przypadek, w którym V jest wielomianem dowolnego stopnia względem x.

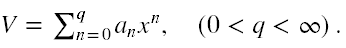
Poszukiwał rozwiązań w tej samej postaci jak Sauter.

Autorem trzeciej próby był Vernon Myers [27]. Przyjął on, że rozwiązanie powinno mieć postać

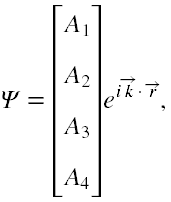
gdzie A₁, A₂, A₃, A₄ są funkcjami czasu , k_x = k_0x +ϵEt/ℏ, k_y = k_0y, k_z = k_0z, ϵ to ładunek elektryczny, E to pewna stała, k_0x, k_0y, k_0z to także stałe. Składowe A₁, A₂, A₃, A₄, które on otrzymał były dosyć skomplikowane, miały postać szeregu potęgowego i eksponentu.

I autorami ostatniej próby, którą znaleźliśmy, są Fradkin, Gitman i Shvartsman [28]. Oni badali zewnętrzne pole elektromagnetyczne, które jest złożeniem równoległych pól elektrycznego i magnetycznego danych przez potencjały (¹¹)

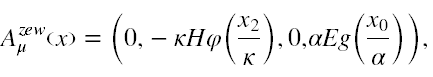
gdzie φ i g są dowolnymi funkcjami, a κ i α są parametrami kontroli wymiaru.

Potencjał ten daje następujące natężenia pól

E_x = E_y = H_x = H_y = 0,

E_z = Eg', H_z = Hφ'.

Celem uzyskania stałego pola elektrycznego należy przyjąć

g(x₀/α) = x₀/α.

Aby rozwiązać równanie Diraca autorzy [28] użyli ogólnej metody podanej w §32 podręcznika [15], gdzie wykorzystuje się tzw. kwadratowe równanie Diraca i zapostulowali, że jego rozwiązanie ma następującą postać

ψ(x) = L^-1 e^{-i[p₁x1+p₃x3/ℏ]}f_λ²,ζ(x₂)χ(x⁰)u_ζ, (24)

gdzie p₁ i p₃ są wartościami własnymi operatorów iℏ∂₁ i iℏ∂₃, a u_ζ są bispinorami własnymi macierzy α₃ i Σ₃

Σ₃u_ζ = ζu_ζ, α₃u_ζ = u_ζ, ζ = ±1.

Rozwiązanie zaproponowane przez Vernona Myers’a jest w sposób oczywisty niestacjonarne. Jednak w jego pracy brak jest wyjaśnień dlaczego akurat taką postać ma mieć rozwiązanie. Myers nie badał czy równanie Diraca w jednorodnym polu elektrycznym ma rozwiązania stacjonarne. Z drugiej strony postać zaproponowanej przez niego niestacjonarnej funkcji falowej oznacza narzucenie bardzo mocnych ograniczeń na postać rozwiązania. Wiązać się z tym powinno szczegółowe umotywowanie zasadności takiego postępowania.

Pozostali autorzy poszukiwali rozwiązań o rozdzielonych zmiennych, w tym pierwsi dwaj do tego stacjonarnych. Jednak nikt z nich nie badał, czy analizowany przez nich przypadek równania Diraca dopuszcza rozwiązania o rozdzielonych zmiennych.

Zwrócimy bardziej uwagę na ostatni przykład i zacytujemy tu postać kwadratowego równania Diraca, którą autorzy [28] analizowali. Ma ona formę

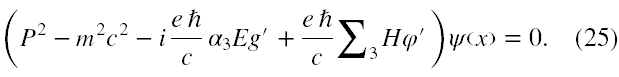
Jednak zawarty w nim wyraz P² to operator różniczkowy mający postać [15]

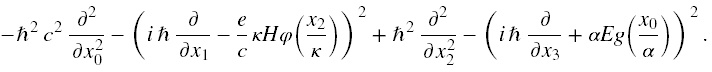
Jak widać występują w nim wyrazy mieszające zmienne x₁ i x₂ oraz x₀ i x₃. Zatem na pierwszy rzut oka można sobie wyobrazić możliwość rozdzielenia zmiennych tylko parami, czyli

ψ(x) = f(x₁,x₂)χ(x₀,x₃),

a stąd nie całkowicie.

Jak wynika z [29] istnieją w miarę proste metody pozwalające na uzyskanie rozwiązań, w których zmienna czasowa jest oddzielona od zmiennych przestrzennych (metoda Fouriera dla wielu zmiennych niezależnych), ale warunkiem jest niewystępowanie przy pochodnych przestrzennych współczynników będących funkcjami zmiennej czasowej. W przypadku równania (25) tak nie jest. Stąd naszym zdaniem przed skorzystaniem z podstawienia (24) należałoby podać dowód dopuszczalności takiego rozwiązania.

UWAGI

(¹) Zwyczajowo oznaczany symbolem Ψ i nazywany funkcją falową.

(²) Szerszy przegląd własności stanów stacjonarnych zawarty jest przykładowo w §8 książki Schiffa [7], §16 Dawydowa [8], §30 Błochincewa [9].

(³) Tak definicję stanu stacjonarnego podają Weyl [10], Dawydow [8], Landau i Lifszyc [11], Messiah [12] natomiast Schiff [7], Średniawa [20], Błochincew [9], Burkhardt i Leventhal [19], Sakurai [18], Merzbacher [17], Liboff [16] podkreślają, że istotnym jest niezależność od czasu gęstości prawdopodobieństwa znalezienia cząstki, jak i innych prawdopodobieństw.

(⁴) Ponadto układ opisywany przez H₀ musi być konserwatywny, a stany całego układu muszą się dać skonstruować jako superpozycja rozwiązań zagadnienia niezaburzonego, Merzbacher [17].

(⁵) Prezentowana tu metoda Fouriera rozwiązywania równań różniczkowych cząstkowych jest jedynie sposobem na zbadanie czy jest dopuszczalnym poszukiwanie rozwiązań równania różniczkowego w formie ψ(x,y,z)∙ω(t). Jako, że równanie Schrödingera zawiera tylko jedną i do tego pierwszego rzędu pochodną po czasie łatwo może dochodzić do utożsamienia zagadnienia rozdzielenia zmiennej czasowej od zmiennych przestrzennych z problemem znajdowania stanów stacjonarnych.

(⁶) Ładunek elektronu tu zgodnie z notacją kursu Fizyki Teoretycznej Landaua i współpracowników to e = -|e|.

(⁷) Autorzy [11] w ogóle tego nie badają, ten fragment rachunków pochodzi od nas.

(⁸) Chociaż energia stanu stacjonarnego jest tutaj stałą równą ε, to jednak zgodnie z postacią operatora energii kinetycznej Ê= iℏ∂/∂t-eA⁰ dla cząstki w polu, energia kinetyczna elektronu w tym przypadku jest równa ε+eEx.

(⁹) Poprawiliśmy trochę opis tej metody pochodzący z książki W. Smirnowa, aby stał się on naszym zdaniem bardziej przejrzysty. W tym celu w szczególności dodaliśmy wzór pośredni (16), który autor pominął jako zapewne zbyt oczywisty. Przedstawiona metoda należy do klasyki teorii równań różniczkowych, bo podręczniki nie wskazują jej autora. Jej opis w formie twierdzenia z dowodem znajduje się także w §1 rozdziału VII podręcznika [22]. Ponieważ podręczniki mechaniki kwantowej milczą na temat tej metody postanowiliśmy zamieścić tutaj jej szczegółowy opis.

(¹⁰) W równaniach tych jeszcze nie zostało sprecyzowane, czy badamy elektron, czy też pozyton.

(¹¹) Tutaj notacja jest zaczerpnięta z [28].

LITERATURA

[1] J. Szcząchor, On the wave function of relativistic electron moving in a uniform electric field, https://www.researchgate.net/, Rozwiązanie równania Diraca w jednorodnym polu elektrycznym - część 1, Rozwiązanie równania Diraca w jednorodnym polu elektrycznym - część 2, Quasi-klasyczna interpretacja rozwiązań równania Diraca w jednorodnym polu elektrycznym.

[2] H. A. Enge, M. R. Wehr, J. A. Richards, Introduction to Atomic Physics, Addison-Wesley, 1973.

[3] N. Bohr, On the constitution of atoms and molecules, Philosophical Magazine, Series 6, 26: 151 (1913), s. 1 — 25.

[4] Z. Strugalski, O zasadzie nieoznaczoności Heisenberga, Kwartalnik Historii Nauki i Techniki 24r/2, 355-366, 1979.

[5] P. Weinberger, Niels Bohr and the dawn of quantum theory, Philosophical Magazine, 2014; http://dx.doi.org/10.1080/14786435.2014.951710.

[6] D. L. Anderson, The Discovery of the Electron, D. Van Nostrand Company, Inc., 1964, Princeton N.J.

[7] L. Schiff, Quantum Mechanics, McGraw-Hill Book Company, New York, 1968.

[8] A. Dawydow, Mechanika kwantowa, PWN, Warszawa 1969.

[9] D. Błochincew, Podstawy mechaniki kwantowej, PWN, Warszawa 1954.

[10] H. Weyl, The Theory of Groups and Quantum Mechanics, Dover Publications, Inc, 1931.

[11] L.D. Landau, E.M. Lifshitz, Quantum Mechanics, Non-relativistic Theory, Pergamon, Oxford, 1958.

[12] A. Messiach, Quantum Mechanics, Volume I, North-Holland Publishing Company, Amsterdam 1967.

[13] P. A. M. Dirac, The Principles of Quantum Mechanics, Pergamon, Oxford, 1958.

[14] J. D. Bjorken, S. D. Drell, Relativistic Quantum Mechanics, McGraw-Hill, New York, 1964.

[15] V. B. Berestetskii, E. M. Lifschitz, L. P. Pitaevskii, Relativistic Quantum Theory, Part I, Pergamon, Oxford, 1971.

[16] R. Liboff, Introductory Quantum Mechanics, Addison-Wesley Publishing Company, 1980.

[17] E. Merzbacher, Quantum Mechanics, John Wiley & Sons, 1988.

[18] J. Sakurai, J. Napolitano, Modern Quantum Mechanics, Addison-Wesley Publishing Company, 2011.

[19] C. Burkhardt, J. Leventhal, Foundations of Quantum Physics, Springer, 2008.

[20] B. Średniawa, Mechanika Kwantowa, PWN, Warszawa 1981.

[21] W. Pogorzelski, Analiza matematyczna, Tom IV, PWN, Warszawa 1956.

[22] W. Stiepanow, Równania różniczkowe, PWN, Warszawa 1956.

[23] W. I. Smirnow, Matematyka wyższa, Tom II, §10, PWN, Warszawa 1963.

[24] L. Evans, Partial Differential Equations, American Mathematical Society, 1998.

[25] F. Sauter, Über das Verhalten eines Elektrons im homogenen elektrishen Feld nach der relativistischen Theorie Diracs, Z. f. Physik 69 (1931) 742.

[26] M. S. Plesset, The Dirac Electron in Simple Fields, Phys. Rev. 41 (1932) 278.

[27] V. W. Myers, Solutions of the Time-Dependent Klein-Gordon and Dirac Equations for a Uniform Electric Field, JOURNAL OF RESEARCH of the National Bureau of Standards - B. Mathematical Sciences 72 B No. 1 (1968) 37.

[28] E. S. Fradkin, D. M. Gitman, Sh. M. Shvartsman, Quantum electrodynamics with unstable vacuum,Chapter 5.1 Processes in an Electric Field, Berlin, Springer (1991).

[29] W. M. Babicz, M. B. Kapilewicz, S. G. Michlin, G. N. Natanson, P. M. Riez, L. N. Słobodecki, M. M. Smirnow, Równania liniowe fizyki matematycznej, Warszawa, PWN, 1970.