Rachunek różniczkowy i całkowy w fizyce szkolnej - część 9

Szczegóły
Kategoria: Rachunek różniczkowy i całkowy w fizyce szkolnej
Opublikowano: środa, 16, listopad 2016 15:55
Autor : Janusz Szcząchor

zadanie nr 5.64 , Bogdan Mendel, Janusz Mendel - "Zbiór zadań z fizyki", WSiP, Warszawa 1976

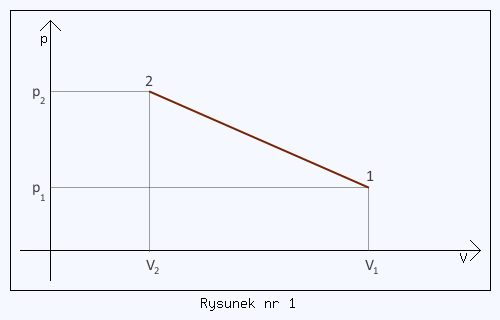
Hel o masie m = 20 g poddano powolnej przemianie gazowej, której wykres podano na rysunku 5.15. Jaką największą temperaturę miał gaz w tym procesie (V1 = 32 dm3, p1 = 4,1 atm, V2 = 8 dm3, p2 = 16,4 atm)?

Rozwiązanie

O helu musimy założyć, na tym etapie nauki fizyki, że jest gazem doskonałym. Równanie Clapeyrona jest wtedy podstawowym równaniem wiążącym jego ciśnienie, objętość i temperaturę ze sobą. Z treści zadania można wysnuć wniosek, że hel poddano przemianie gazowej, która nie jest ani izochoryczną, ani izobaryczną, bo to wynika z poniższego wykresu - patrz rysunek nr 1, na którym przedstawiono zależność między ciśnieniem helu, a jego objętością w czasie tej przemiany gazowej.

zależność p od V w przemianie gazowej

Co więcej, skoro mamy ustalić największą temperaturę helu w tym procesie, to raczej nie była ona stała, bo takie pytanie byłoby wtedy bezprzedmiotowe. W tej sytuacji znacznym ułatwieniem w analizie zadania będzie przypomnienie równania Clapeyrona

pV = (m/μ)RT , (1)

gdzie μ - to masa molowa danego gazu. Na podstawie tego wzoru możemy napisać, że temperatura helu na dowolnym etapie wskazanej przemiany, to jest dla dowolnej pary wartości p i V jest dana jako

T = μpV/(mR) . (2)

Z kolei na podstawie wykresu z rysunku nr 1 możemy zauważyć, że w tej przemianie ciśnienie helu jest liniową funkcją jego objętości, a zatem temperatura powinna być funkcją kwadratową tej zmiennej. Tym samym poszukiwanie temperatury maksymalnej helu w tym procesie można by sprowadzić do obliczeń algebraicznych, gdyby udało się podać zależność p od V dla helu w formie analitycznej, czyli wzorem.

Zauważmy, że prosta dana na rysunku nr 1 przechodzi przez dwa ustalone punkty. Stąd da się ustalić jej równanie na podstawie geometrii analitycznej. Zgodnie z (1) prosta nieprostopadła do osi OX i przechodząca przez dwa dane, różne punkty P1(x1,y1) i P2(x2,y2) ma równanie

równanie prostej przechodzącej przez dwa punkty

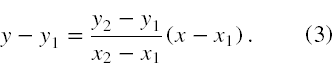
Utożsamiając zmienną y z p, a x z V możemy zapisać, że ciśnienie jest następującą funkcją objętości

p jako funkcja liniowa V

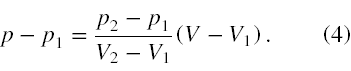
Dla uproszczenia obliczeń zapiszmy równanie (4) w formie

p = aV + b, (5)

gdzie jako a, współczynnik kierunkowy prostej będzie oznaczone poniższe wyrażenie

współczynnik kierunkowy prostej

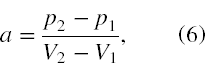
natomiast jako wyraz wolny b przyjmiemy

wyraz wolny

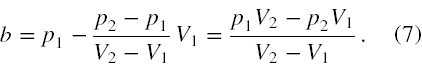
W takiej sytuacji wyrażenie (2) na temperaturę helu przyjmie postać

T = (μ/mR)(aV+b)V . (8)

Dla większej czytelności wprowadźmy dodatkowe oznaczenia. Niech jako c będzie przyjęta wielkość

współczynnik c

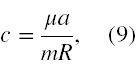
a jako d wielkość poniższa

współczynnik d

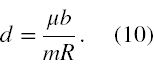
Wtedy równanie (8) będzie można zapisać w formie łatwej do analizy, czyli

T(V) = cV2 + dV . (11)

Maksimum funkcji T(V) będziemy poszukiwać w sposób standardowy (2). Zaczniemy od warunku koniecznego ekstremum, czyli przyrównamy pierwszą pochodną temperatury T względem objętości V do zera

przyrównanie pierwszej pochodnej T do zera

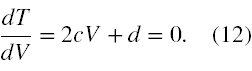
Zatem punktem podejrzanym o maksimum jest

V = - d/2c = - b/2a . (13)

Następnie bierzemy pod uwagę warunek wystarczający ekstremum, czyli obliczamy drugą pochodną funkcji temperatury helu względem objętości, która jest równa

d2T/dv2 = 2c . (14)

Teraz musimy zbadać znak drugiej pochodnej w punkcie podejrzanym o ekstremum. Jednak druga pochodna jest oczywiście funkcją stałą dla funkcji kwadratowej. Wchodzące w skład stałej c (9) wielkości μ, m, R są rzecz jasna dodatnie. Stąd jest tylko pytanie o znak a danego wzorem (6) dla danych naszego zadania. Krótka analiza tego wyrażenia daje odpowiedź, że a jest ujemne. Zatem

2c < 0 (15)

i dla objętości danej wyrażeniem (13) mamy maksimum.

Aby poznać wartość maksymalnej temperatury helu musimy po pierwsze do wyrażenia (11) podstawić wyrażenie (13), następnie podstawić odpowiednie wyrażenia za a, b, c, d i otrzymujemy

temperatura maksymalna helu

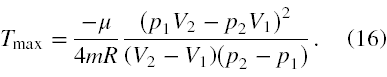
Interesującym jest poznanie wartości objętości i ciśnienia, dla których mamy maksimum temperatury helu. Z (13), (6) i (7) mamy, że

objętość dla T maksimum

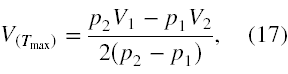
a z (5) i (13) otrzymujemy

ciśnienie dla T maksimum

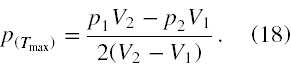
Zauważmy, na podstawie danych zadania (patrz treść), że akurat w tym zadaniu mamy spełnioną równość, że

p1V1 = p2V2 . (19)

Korzystając z tej własności, (należy wzór 18 pomnożyć przez (p1 + p2)/(p1 + p2), a wzór 17 przez (V1 + V2)/(V1 + V2) oraz skorzystać w mianowniku z równości (19) ) można pokazać, że

V(Tmax) = (V1 + V2)/2 , (20)

oraz że,

P(Tmax) = (p1 + p2)/2 . (21)

W ten sposób wzór (16) na maksymalną temperaturę helu przyjmuje postać

wzór na temperaturę maksymalna helu

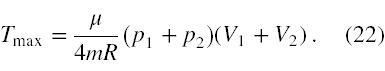
Aby obliczyć tę temperaturę, wzór (22), nie możemy tak wprost podstawić danych zadania. Pamiętając, że 1 atmosfera fizyczna to 101325 N/m2, a 1 dm3 to 0,001 m3 oraz, że masa molowa helu to mniej więcej 4 g/mol otrzymujemy, że

Tmax ≈ 499,92 K . (23)


LITERATURA

1 W. Leksiński, B. Macukow, W. Żakowski - Matematyka w zadaniach, Dla kandydatów na wyższe uczelnie, Wydawnictwo Naukowo - Techniczne, Warszawa 1981. §10.2. Prosta na płaszczyźnie

2 W. Leksiński, B. Macukow, W. Żakowski - Matematyka w zadaniach, Dla kandydatów na wyższe uczelnie, Wydawnictwo Naukowo - Techniczne, Warszawa 1981. §9.5. Ekstrema funkcji