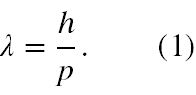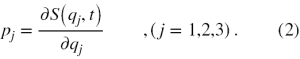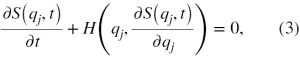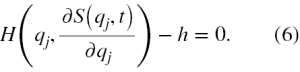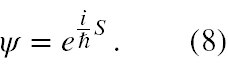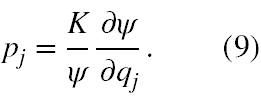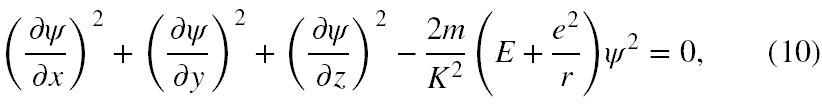Autor: Janusz Szcząchor

Chociaż obecnie nie omawia się na lekcjach fizyki w szkole średniej, nawet na poziomie rozszerzonym, zasady nieoznaczoności Heisenberga, to można spotkać w czasopismach popularnonaukowych artykuły starające się przybliżyć to zagadnienie.

Jako przykład może posłużyć artykuł “Wokół zasady nieoznaczoności” Jana Chwedeńczuka [1]. Informuje on czytelnika, iż powszechnie uznane i nie budzące kontrowersji sformułowanie zasady nieoznaczoności Heisenberga mówi, że nie można przygotować cząstki w takim stanie kwantowym, by zarówno jej położenie, jak i pęd były określone, a następnie przedstawia eksperyment myślowy wyjaśniający istotę zagadnienia.

Jednak załóżmy, że nasz czytelnik (młody) zna już rachunek różniczkowo-całkowy i mówi, że go to nie przekonuje, że chce zobaczyć rachunki matematyczne. Co możemy mu wówczas zaproponować?

Można zaryzykować tezę, że każdy “porządny” podręcznik mechaniki kwantowej dla studentów, taki jak [2-3,6-8] zawiera elementarny dowód zasady nieoznaczoności.

Jednak jak się dobrze przyjrzeć taki dowód zawiera nie tylko jawne założenie, że funkcja falowa jest całkowalna w kwadracie, ale także domyślne założenia, że operatory są hermitowskie, a ich wartości własne są rzeczywiste.

Jak pokażę to dalej nie dla każdej funkcji falowej założenia te są spełnione. A zatem dla niektórych stanów kwantowych układu fizycznego nie da się udowodnić spełnienia zasady nieoznaczoności. Tak więc znika obraz tej zasady jako powszechnie obowiązującego prawa fizyki. Co gorsza nie tylko laikom, ale nawet studentom fizyki nie podaje się tej informacji. Celem mojego artykułu jest właśnie zwrócenie uwagi na tą “piętę achillesową” zasady Heisenberga.

Wybrane pojęcia z podstaw mechaniki kwantowej

Jako literaturę uzupełniającą do tego fragmentu naszego artykułu polecamy stosunkowo nowy podręcznik mechaniki kwantowej S. Szpikowskiego [2] oraz szeroko znane pozycje L. Schiffa [3] i P. Diraca [4]. Ponadto zakładamy, że czytelnik zna już treść naszego artykułu “Co to jest funkcja falowa i po co jej używamy?“.

W mechanice kwantowej każda wielkość fizyczna jest reprezentowana przez operator. Dla ruchu cząstki wzdłuż osi x jej operator pędu to

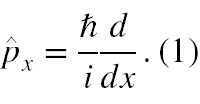
Aby poznać wartość pędu cząstki należy tym operatorem zadziałać na funkcję falową (wektor stanu) cząstki zgodnie z poniższym równaniem, zwanym równaniem własnym operatora, w którym wartość pędu ma być stałą wartością p

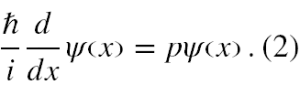
Jest to równanie różniczkowe (¹), którego rozwiązaniem jest funkcja falowa następującej postaci

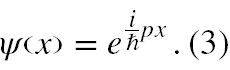
Jeżeli ta funkcja falowa, miałaby mieć interpretację probabilistyczną (²), to całka po całej przestrzeni z jej kwadratu modułu, tj. |ψ|² = ψ^*ψ powinna dać się unormować (³) do 1. Jednak tu kwadrat modułu jest stale równy 1, a stąd wartość takiej całki to +∞. Stąd podzielenie takiej funkcji przez dowolną stałą nie ma wpływu na wartość takiej całki. Stawia to pod znakiem zapytania tezę, że taka funkcja falowa (⁴) może być nośnikiem informacji o prawdopodobieństwie zajścia jakiegoś procesu fizycznego .

Funkcja delta Diraca

Paul Dirac pracując nad problemem funkcji falowych mających widmo ciągłe (⁵) wprowadził pojęcie funkcji δ(x), zwanej później deltą Diraca. Z definicji ma ona następujące własności:

dla x ≠ 0 oraz

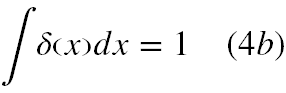
dla przedziału całkowania obejmującego położenie x = 0.

Jak podają podręczniki [2-3] (a także inne podręczniki mechaniki kwantowej), przy pomocy tej funkcji da się wyrazić związki ortogonalności (⁶) funkcji falowych (3) jako

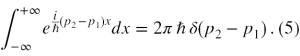
Jednak to nie oznacza, że równanie (5) jest tożsame z nadaniem funkcjom (3) interpretacji probabilistycznej (⁷). Aby tak było ∫ψ(x)^*ψ(x)dx musi być równa liczbie, a nie funkcji, bo prawdopodobieństwo jest liczbą z przedziału <0,1>.

Jak można przeczytać w [3] Dirac wyobrażał sobie, że δ(x) to funkcja wszędzie równa 0 za wyjątkiem małego przedziału o długości ε otaczającego początek układu x = 0, gdzie w tym przedziale jest ona na tyle duża, że jej całka po tym przedziale jest równa 1.

Wyjaśniał dalej, że jest to funkcja niewłaściwa, czyli coś bardziej ogólnego niż zwykła funkcja, że może być stosowana tylko w pewnym typie wyrażeń, aby nie doszło do niespójności, nielogiczności teorii.

W szczególności wskazywał, że podstawowym jej zastosowaniem powinny być wyrażenia postaci

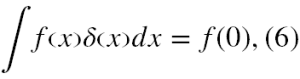
gdzie δ(x) występuje jako wyrażenie podcałkowe. Zatem równości typu (5) powinny mieć zastosowanie pod znakiem całki (⁸), a nie być interpretowane jako wyrażenia samodzielne.

Reasumując uważamy, że funkcje falowe postaci (3) nie mają interpretacji probabilistycznej i przy ich pomocy nie można obliczyć prawdopodobieństwa znalezienia cząstki o pędzie p_x w położeniu x. Dokładniejsze nasze poglądy na interpretację tych funkcji falowych zawarliśmy w artykułach “Czy cząstka kwantowa może poruszać się klasycznym torem ruchu? – część 1 i część 2“.

Sformułowanie zasady nieoznaczoności

Oczywiście nie będziemy tutaj przytaczać pełnych rachunków prowadzących do sformułowania zasady nieoznaczoności, ale zacytujemy najważniejsze elementy dowodu oparte głównie na [2], paragraf 2.3.5.

Wartość oczekiwana ā (względnie średnia pomiarów), pewnej wielkości fizycznej, którą reprezentuje operator Â, dla stanu układu opisanego unormowaną funkcją falową ψ jest dana jako

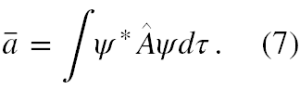
Załóżmy, że mamy jeszcze jeden operator Ô, niekomutujący (⁹) z operatorem Â. Jego wartość oczekiwana ō w stanie ψ, to oczywiście

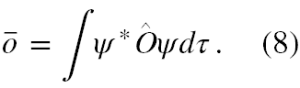
Niech ψ będzie dowolną unormowaną funkcją falową, ale założymy, że w ogólności nie jest ona funkcją własną któregokolwiek z operatorów  lub Ô. W tym stanie, dla każdego z powyższych operatorów można zdefiniować uśredniony po wszystkich pomiarach kwadrat odchylenia pomiarów od wartości średniej. Będą to wielkości odpowiednio dane wzorami

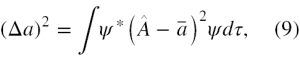
oraz

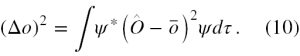
Będziemy szukać ograniczenia od dołu iloczynu “rozrzutów” pomiarów wielkości fizycznych reprezentowanych przez te dwa niekomutujące operatory tj. iloczynu (Δa)² ·(Δo)².

Rozwiązaniem jest lemat, który mówi, że dla dowolnych dwóch funkcji u i v całkowalnych w kwadracie zachodzi następująca nierówność

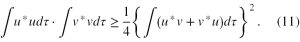
Jeżeli za funkcje u i v przyjmiemy u = (Â-ā)ψ ,v = i(Ô-ō)ψ  i podstawimy je do (11), to po wykonaniu kilku przekształceń otrzymamy, że

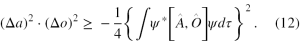
W kolejnych częściach naszego artykułu będziemy analizować wnioski wypływające ze wzoru (12) po zastosowaniu go do wybranej funkcji falowej oraz konkretnej pary niekomutujących operatorów.

Zasada nieoznaczoności a atom wodoru

Poszukiwanie funkcji falowych opisujących zachowanie się elektronu w atomie wodoru to zagadnienie dwóch ciał, kwantowy analog klasycznego problemu dwóch ciał (¹⁰). Zagadnienie to rozwiązuje się w układzie współrzędnych kulistych §14 w [3]. Rozwiązanie ma wówczas postać u_nlm(r,θ,φ) = R_n,l(r) · Y_lm(θ,φ), §16 w [3].

Radialna część funkcji falowej to R_n,l(r) = e^-ρ/2 ρ^l L^2l+1_n+l(ρ),
gdzie ρ = 2Zr/na₀, a₀ = ħ²/μe², L^2l+1_n+l(ρ) – stowarzyszone wielomiany Laguerre’a, a μ to masa zredukowana układu jądro – elektron.

Z kolei Y_l,m(θ,φ) = (-1)^m[(2l+1)(l-|m|)!/4π(l+|m|)!]^1/2 P_l^m(cosθ) e^imφ, gdzie P_l^m(cosθ) to wielomiany Legendre’a.

Interesować nas będą własności stanu 1s, w którym n = 1, l = 0, m = 0. Wówczas, stosując oznaczenia z [3], funkcja falowa tego stanu to
u_1,0,0 = (πa³₀)^-1/2 e^-r/a₀. Jak można w prosty sposób sprawdzić funkcja ta istotnie jest unormowana (¹¹).

W tym momencie możemy już przystąpić do sprawdzenia słuszności zasady nieoznaczoności dla wybranej pary operatorów w stanie 1s. Operator pędu we współrzędnych sferycznych ma postać (przykład 1b, §14.107 w [9])

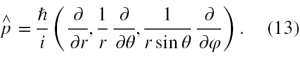
Natomiast operator położenia w tych samych współrzędnych to

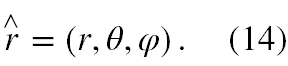
Komutator r-tych składowych tych operatorów łatwo policzyć pamiętając, że on także jest operatorem, a więc powinien być obliczany podczas działania na funkcję falową. Jest on równy

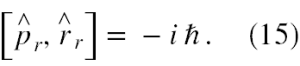
Prawa strona wzoru (12), po uwzględnieniu, że interesującym nas komutatorem jest (15), który działa na stan u_1,0,0 jest równa

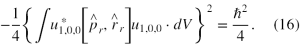
Aby obliczyć lewą stronę (12) przy tych samych założeniach będziemy musieli policzyć wartości oczekiwane r-tych składowych operatorów położenia i pędu oraz ich kwadratów. W przypadku operatora położenia mamy (¹²):

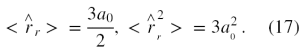
Wartość oczekiwana pędu radialnego to (¹³)

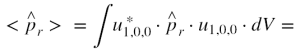
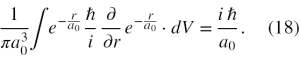
Nie powinno zatem ulegać wątpliwości, że wartość oczekiwana operatora kwadratu pędu radialnego jest równa -ħ²/(a₀)².

Jak pokazuje elementarny rachunek,  uśredniony po wszystkich pomiarach kwadrat odchylenia pomiarów od wartości średniej dla operatora pędu radialnego jest równy 0 (¹⁴), natomiast ta sama wielkość dla operatora położenia radialnego jest równa 3a₀²/4  (¹⁵).

Podstawiając wyniki obliczeń do (12), wstawiając jawnie a₀ (¹⁶) otrzymujemy

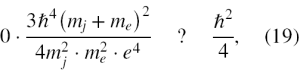
skąd widzimy, że zasada nieoznaczoności w tym przypadku nie zachodzi.

Zasada nieoznaczoności a cząstka swobodna

Podsumowanie

---

(¹) Jest to najprostsze równanie różniczkowe zwane liniowym jednorodnym. Metody jego rozwiązywania uczy się w szkole średniej na matematyce, przynajmniej na poziomie rozszerzonym.

(²) Interpretacja probabilistyczna (statystyczna) funkcji falowej zakłada, że ψ(x)^*ψ(x) jest gęstością prawdopodobieństwa położenia cząstki w punkcie x, a ψ(x)^*ψ(x)dx jest prawdopodobieństwem znalezienia cząstki w przedziale dx wokół położenia x. Sumując (całkując) prawdopodobieństwa po wszystkich dopuszczalnych położeniach musimy dostać pewność, czyli 1. Wyraża to ideę, że cząstka istnieje.

(³) Załóżmy, że całka ∫ψ(x)^*ψ(x)dx nie jest równa 1, ale jest skończona i równa a². Wtedy przyjmując podstawienie ψ₁(x) = ψ(x)/a otrzymujemy nową funkcję falową ψ₁(x), która już spełnia warunek ∫ψ₁(x)^*ψ₁(x)dx = 1. Co więcej taka funkcja również spełnia równanie własne (2) do tej samej wartości własnej.

(⁴) Mimo niespełniania warunku normowalności do 1 jest to nadal funkcja falowa, bo spełnia równanie (2), a ponadto może poprawnie opisywać np. zjawisko interferencji.

(⁵) Przykładem funkcji falowej mającej widmo ciągłe jest właśnie (3). Zbiór dopuszczalnych wartości pędu (a co za tym idzie i energii) tej funkcji jest tożsamy ze zbiorem liczb rzeczywistych. Przeciwieństwem jest funkcja falowa mająca widmo dyskretne. Są nimi np. funkcje falowe elektronu w stanie związanym w atomie wodoru, bo odpowiadające im dopuszczalne wartości energii (atomu wodoru) można ponumerować kolejnymi liczbami naturalnymi.

(⁶) Z lekcji matematyki i fizyki w szkole średniej powinieneś pamiętać, że dwa wektory są do siebie prostopadłe, gdy ich iloczyn skalarny jest równy 0. Natomiast iloczyn skalarny wektora samego ze sobą to kwadrat jego długości.

Dla dowolnych funkcji falowych φ(x) i ψ(x) też da się zdefiniować iloczyn skalarny. Jest to wyrażenie oznaczane jako <φ|ψ> i równe ∫φ^*(x)ψ(x)dx. Jeżeli <φ|ψ> = 0, to mówimy, że dwie funkcje falowe są do siebie ortogonalne (prostopadłe), a kiedy <ψ|ψ> = 1, to mówimy, że funkcja falowa jest unormowana. Jeden wzór matematyczny łączący te obie własności nazywamy związkiem ortonormalności.

(⁷) Jako ilustrację trudności z nadaniem funkcjom (3) interpretacji probabilistycznej zacytujmy dwóch autorów.

S. Szpikowski na stronie 47 w [2] pisze:
“Równość (2.28) pokazuje, że funkcje własne operatora położenia są ortogonalne. Natomiast, zamiast unormowania do funkcji δ Kroneckera, otrzymaliśmy „unormowanie” do funkcji δ Diraca. Takie „unormowanie” będzie występowało wszędzie tam, gdzie widmo wartości własnych będzie widmem ciągłym.
Cudzysłów „unormowania” ma podkreślać fakt, że nie można tu mówić o właściwym unormowaniu prowadzącym zawsze do wektorów o jednostkowej długości. Wynik (2.28) pokazuje, że funkcje własne ψ (2.27) są „wektorami” o nieskończonej długości, a więc nie mogą być elementami przestrzeni Hilberta.

Z kolei A. Dawydow na stronie 42 w [6] pisze:
“Być może, nienormalizowalność funkcji własnych

(∫|ψ_F(ξ)|²dξ=∞)

operatorów o widmie ciągłym jest związana właśnie z tym, że odpowiednich stanów nie można urzeczywistnić. Praktycznie można urzeczywistnić tylko takie stany, w których wartość F leży w pewnym przedziale F, F+ΔF. Stany takie są opisywane pakietami fal typu (10.7), które można normować. “

(⁸) Jest to z pewnością doskonałe narzędzie do prowadzenia obliczeń w relatywistycznym rachunku zaburzeń powstałym przy pomocy teorii propagatorów [5], gdzie pozwala to na łatwe wyrażenie zasady zachowania czteropędu w języku funkcji falowych.

(⁹) Dla dwóch operatorów  i Ô można zdefiniować trzeci operator zwany ich komutatorem [Â,Ô] w ten sposób, że z definicji jest on równy [Â,Ô] = ÂÔ-ÔÂ. Jeżeli komutator jest równy 0, to mówimy, że operatory ze sobą komutują. Dla bezpieczeństwa wartość komutatora należy obliczać zawsze w działaniu na jakąś funkcję falową.

(¹⁰) .

(¹¹) Dowód, że stan 1s jest unormowany.

(¹²) Obliczenie wartości oczekiwanych dla operatora położenia.

(¹³) Należy się tu dygresja. Jak dowodzi się np. w [7] §6.3. operator pędu jest operatorem hermitowskim, a więc powinien mieć rzeczywiste wartości własne (a nie urojone). Gdzie tkwi “błąd”?

Powyższy dowód jest oparty na tym, że równanie własne operatora i równanie do niego sprzężone dają tę samą wartość własną. Tak jest dla funkcji falowych zespolonych, których wewnętrzna zmienna jest urojona (patrz funkcje własne operatora pędu do rzeczywistej wartości własnej). Tak naprawdę operator pędu jest hermitowski tylko dla zespolonych funkcji falowych, dla rzeczywistych jest skośnie hermitowski i daje wtedy wartości własne urojone. Rozwiązując równanie własne (2) milcząco założyliśmy, że wartości własne są rzeczywiste.  

Powstaje oczywiście pytanie jaki jest sens fizyczny urojonej wartości własnej operatora pędu? Przestrzegalibyśmy przed przyjęciem, że jest po prostu równa 0, albowiem np. wartość momentu pędu (a raczej pierwiastek kwadratowy z wartości własnej operatora kwadratu momentu pędu) w stanie u_1,0,0 jest właśnie równy 0. Naszym zdaniem najprawdopodobniej należy przyjąć, że pęd radialny w tym stanie jest nieokreślony. Jak wskazaliśmy w artykule  Czy wszystko już wiemy o związanych stanach stacjonarnych? – Część 3 pęd radialny dla elektronu w polu Coulomba nie komutuje z hamiltonianiem, zatem nie jest tutaj całką ruchu.

(¹⁴)Obliczenia – uśredniony po wszystkich pomiarach kwadrat odchylenia pomiarów od wartości średniej dla operatora pędu radialnego.

(¹⁵) Obliczenia – uśredniony po wszystkich pomiarach kwadrat odchylenia pomiarów od wartości średniej dla operatora położenia radialnego.

(¹⁶) Masa zredukowana układu jądro-elektron, to μ = m_j⋅m_e/(m_j+m_e), patrz §16 w [3].

Literatura

[1] J. Chwedeńczuk – Wokół zasady nieoznaczoności, Delta 10/2017.
[2] S. Szpikowski, Podstawy Mechaniki Kwantowej, WUMCS, Lublin 2011.
[3] L. Schiff, Mechanika kwantowa, PWN, Warszawa, 1977.
[4] P. A. M. Dirac, The Principles of Quantum Mechanics, Pergamon, Oxford, 1958.
[5] J. D. Bjorken, S. D. Drell, Realtywistyczna teoria kwantów, PWN, Warszawa, 1985.
[6] A. Dawydow, Mechanika kwantowa, PWN, Warszawa 1969,
[7] B. Średniawa, Mechanika kwantowa, PWN, Warszawa 1981,
[8] D. Błochincew, Podstawy mechaniki kwantowej, PWN, Warszawa 1954,
[9] E. Karaśkiewicz, Zarys teorii wektorów i tensorów, PWN, Warszawa 1974.