Tag: równanie Hamiltona-Jacobiego

Jeśli ktoś chciałby poznać autorskie wyprowadzenie (¹) równania Schrödingera poprzez po prostu zajrzenie do jakiegoś podręcznika mechaniki kwantowej, to spotka go przykre rozczarowanie. Źródła te prezentują różne wyprowadzenia, ale mają one niewiele wspólnego z tym oryginalnym zawartym w [5]-[8].

Zanim przejdę do sedna problemu warto pokrótce przypomnieć jak w ogóle powstała mechanika kwantowa.

§.1 Kiedy powstała mechanika kwantowa?

Za pierwszą udaną próbę wyjaśnienia widma najprostszego z atomów należy przyjąć teorię Nielsa Bohra i rok 1913. Chociaż teoria ta podawała poprawny układ poziomów energetycznych atomu wodoru, to nie była w stanie podać prawdopodobieństw przejść kwantowych między poszczególnymi poziomami. Wynika to z faktu, że mimo wprowadzenia kwantowania orbitalnego momentu pędu elektronu teoria ta nadal była w zasadzie teorią klasyczną, a co najważniejsze nie posługiwała się jakąkolwiek wielkością fizyczną, której można by użyć bezpośrednio do takich obliczeń.

Prawdopodobieństwa przejść kwantowych, to wielkości mierzalne w fizyce atomowej i w tej sytuacji naturalnym były próby poprawienia teorii Bohra lub zbudowania nowej tak, aby podać ich teoretyczne wyjaśnienie. Jak wskazuje Born [1] udane prace w tym zakresie zaczęły się pojawiać w roku 1921, a trzy lata później Born użył po raz pierwszy pojęcia mechanika kwantowa.

§.2 Jak pojawiło się w fizyce pojęcie funkcji falowej?

Pierwszym przełomem była praca Heisenberga [2], w której autor porzucił obraz orbit elektronowych o określonych promieniach i okresach obiegu, czyli zamiast opisywać ruch elektronu w atomie poprzez podawanie współrzędnej położenia jako funkcji czasu r(t), postawił za cel wyznaczenie macierzy amplitud przejść X_mn między poziomami energetycznymi.

Niestety, mimo wielu kolejnych prac chociażby takich fizyków jak Dirac, czy Pauli takie sformułowanie teorii znane jako mechanika macierzowe było zbyt formalne, a przez to mało zrozumiałe. Trudno było bowiem dostrzec jakie własności, na przykład elektronów powodują, że taka zmiana podejścia jest konieczna.

Rozwiązanie wskazał Louis de Broglie [3], który był przekonany, że w przypadku elektronów również zachodzi dualizm falowo-korpuskularny i z każdą taką cząstką można związać falę płaską o skończonej długości zgodnie ze wzorem

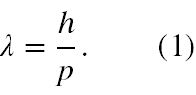
Davisson i Germer [4] oraz inni udowodnili, że rzeczywiście również każda niefotonowa cząstka elementarna ma własności falowe. Jednak wzór (1) dotyczy tylko cząstek swobodnych, a de Broglie nie opisał własności falowych elektronu związanego w atomie. Ze słów Borna w [1] można wyciągnąć wniosek, że po prostu nikt poza Schrödingerem nie wiedział jak to zrobić.

§.3 Oryginalna myśl Schrödingera

Ponieważ Schrödinger wyszedł od opisu mechaniki klasycznej przy pomocy równania Hamilton-Jacobiego, to tytułem wprowadzenia przedstawię podstawowe wiadomości o tym równaniu [9].

A zatem równanie Hamiltona-Jacobiego, to równanie różniczkowe zawierające pochodne cząstkowe, którego rozwiązaniem jest skalarna funkcja S zwana działaniem. Jeśli dla danego układu mechanicznego znamy postać funkcjonalną działania S, to pędy uogólnione tego układu (w przypadku atomu wodoru, gdy źródłem pola elektrycznego jest tylko potencjał skalarny pęd elektronu jest taki sam jak jego pęd uogólniony) są dane jako funkcje położeń q_j i czasu t zgodnie z poniższym wzorem

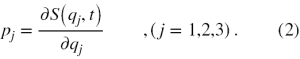
Równanie Hamiltona-Jacobiego w ogólnym przypadku ma postać

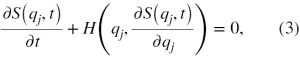
gdzie H, to funkcja Hamiltona. W przypadku, gdy ∂H/∂t = 0 funkcja Hamiltona może być energią układu, czyli

gdzie T, to energia kinetyczna układu, a V to energia potencjalna i funkcja działania S może mieć postać

gdzie h jest pewna stałą. W takiej sytuacji równanie Hamiltona-Jacobiego przyjmuje postać

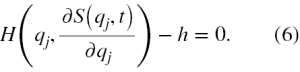
Schrödinger w [1] wyszedł od wzoru (6), gdzie zmienił oznaczenie z h na E i antycypował w ten sposób  fakt, że dopuszczalnych będzie wiele różnych wartości E, które będą tworzyć dozwolone poziomy energetyczne atomu wodoru (²). Dalej wprowadził kolejne własne oryginalne założenia.

Po pierwsze, przyjął on, że funkcja działania S nie jest dalej już niezależną wielkością, a oblicza się ją z innej funkcji ψ według poniższego wzoru (³)

Stałą K wprowadza się na podstawie analizy wymiarowej i musi ona mieć wymiar działania. Kierując się standardową wiedzą z mechaniki kwantowej przekazywaną na przykład na uniwersyteckim wykładzie Mechanika Kwantowa I odwróćmy wzór (7) i mamy, że powinno być

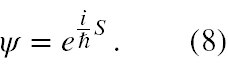
Nie ulega wątpliwości, że Schrödingera funkcja ψ to obecna funkcja falowa, a stała K powinna być równa ħ/i. W ten sposób pęd uogólniony jest dany wzorem

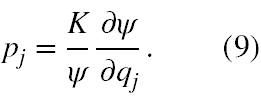
Natomiast równanie (6) staje się równaniem na funkcję ψ. Dla zagadnień nierelatywistycznych energia kinetyczna w funkcji Hamiltona jest kwadratową funkcją pędu (patrz [9]) i równanie (6) w wersji energii potencjalnej dla atomu wodoru, po niewielkim przekształceniu przyjmie postać

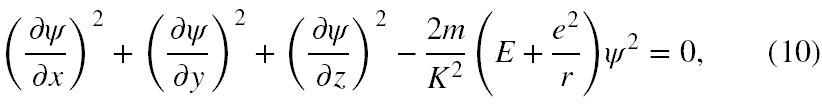
gdzie e = ładunek elektryczny, m = masa elektronu, r² = x² + y² + z². Do tego momentu funkcja ψ będąca rozwiązaniem równania (10) powinna dawać tą samą funkcję działania S, która wynika z równania (6).

Dalsze rachunki Schrödinger przeprowadził zakładając, że funkcja ψ jest wszędzie rzeczywista, jednowartościowa, skończona, różniczkowalna w sposób ciągły do drugiego rzędu.

Wyrażenie po lewej stronie równania (10) uznał za osobną wielkość fizyczną. Dlatego oznaczymy je jako funkcję Z, która jest zależna od ψ oraz jej pochodnych położeniowych ∂ψ/∂x_j

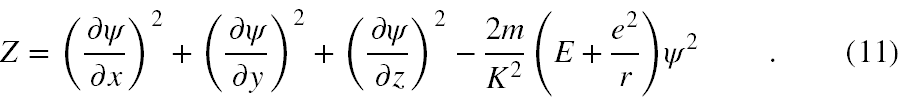
Dalej przyjął, że w przeciwieństwie do mechaniki klasycznej w mechanice kwantowej ta funkcja nie musi być równa 0, a dozwolone wartości tego wyrażenia, a tym samym dozwolone postacie funkcji ψ należy wyznaczyć inaczej.

Funkcję Z (11) uznał za pewnego rodzaju gęstość zależną od położenia i scałkował ją po całej dostępnej przestrzeni (⁴). Tak otrzymaną całkę oznaczmy jako J

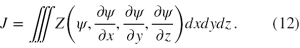
Nie jest ona zwykłą całką, ale funkcją zależną od ψ i jej pochodnych, nazywa się ją funkcjonałem.
W końcu Schrödinger zażądał, aby fizycznie dopuszczalnymi były tylko te funkcje ψ, dla których funkcjonał J przyjmuje wartość ekstremalną. Matematycznie na takie pytania odpowiada rachunek wariacyjny [10], który mówi, po pierwsze, że takie dopuszczalne funkcje ψ muszą być w tym przypadku rozwiązaniami równania postaci

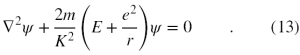
Oraz po drugie, nie mniej ważne, że funkcje ψ muszą przyjmować wartość 0 na powierzchni otaczającej obszar całkowania (czyli w tym przypadku zerować się w nieskończoności).
Przyglądając się równaniu (13) widzimy, że jest to już praktycznie słynne równanie Schrōdingera znane z wykładów mechaniki kwantowej. Pozostaje tylko wykazać, że K = ħ.

§.4 Podsumowanie

Tak naprawdę Schrödinger w swoich pracach [5]-[8] przedstawił dwa wyprowadzenia swojego równania.

O metodzie, którą tu przedstawiłem, powiedział w [6] “…Ta metoda postępowania nie będzie już rozwijana dalej w tej pracy. Naszym celem było tylko podać tymczasowy, szybki przegląd zewnętrznego związku między równaniem falowym i równaniem Hamiltona-Jacobiego. …”. Nieco szerszą analizę tej metody zawarliśmy w artykule Czy wszystko już wiemy o związanych stanach stacjonarnych? – Część 2, gdzie także zacytowaliśmy pogląd Schrödingera na interpretację funkcji falowej.

Druga metoda rozpoczyna się od przedstawienia związków między mechaniką klasyczną w ujęciu Hamiltona, a optyką geometryczną. Ma ona posłużyć dalej uzasadnieniu, że pożądana postać mechaniki kwantowej powinna cechować się takim związkiem formalnym z mechaniką klasyczną jak optyka falowa z optyką geometryczną. Zainteresowanych odsyłam do [6] lub do mojego artkułu W jaki sposób Schrödinger wyprowadził swoje niestacjonarne równanie?, który jest w pewnym sensie moim autorskim tłumaczeniem artykułu [6].

---

(¹) W Internecie można znaleźć stwierdzenia, że równania Schrödingera nie można wyprowadzić, a można je tylko zapostulować. Jednak lektura tego krótkiego artykułu opartego na pracy [5] powinna Cię przekonać, że przedstawione tutaj rozumowanie Schrödingera można nazwać wyprowadzeniem. Podobnie sądzę, że to samo można orzec o jego rozumowaniu zawartym w pracy [8].

(²) Jeżeli będziemy chcieli, jako przykład rozwiązać równanie Hamiltona-Jacobiego dla ruchu ładunku punktowego e w jednorodnym polu elektrycznym E według klasycznej mechaniki relatywistycznej, to jako stałą h należy przyjąć energię spoczynkową ładunku, czyli mc².

(³) Schrödinger w pracy [5] nie wyjaśnił dlaczego dokonał takiego podstawienia. Jednak jeśli wrócimy do wprowadzonej przez de Broglie’a postaci funkcji falowej, to można zauważyć, że w przypadku cząstki swobodnej (która jest opisywana falą płaską), jej faza ma postać k·r-ωt. Biorąc pod uwagę, że k = p/ħ oraz ω = E/ħ można dojrzeć, iż faza tej fali to nic innego jak klasyczne działanie swobodnej cząstki podzielone przez ħ. Dlatego sądzę, że Schrödinger dzięki tej obserwacji doszedł do wniosku, że punktem startowym do wyprowadzenia równania kwantowego na funkcję falową powinno być równanie Hamiltona-Jacobiego w którym dokonać należy podstawienia (7).  Następnie uznał, że tak otrzymane równanie dla szczególnej postaci funkcji falowej powinno być również słuszne dla innych funkcji falowych o postaciach niezgodnych ze wzorem (8).  Ale to wynika już z postulatów fizyki jako teorii. Albowiem jeśli funkcja falowa jest wielkością fizyczną (a przynajmniej chcielibyśmy, żeby taką była), to powinno istnieć jedno ogólne równanie na tą wielkość niezależnie od tego, czy cząstka jest swobodna, czy też porusza się w jakimś potencjale V.

(⁴) Schrödinger w pracy [5] również nie wyjaśnił dlaczego dokonał całkowania zgodnie ze wzorem (12). Aby zrozumieć sens jego postępowania przypomnijmy (patrz np. [11]), że klasyczne działanie to całka po czasie z funkcji Lagrange’a (czyli różnicy energii kinetycznej i potencjalnej) dla klasycznego punktu materialnego, czyli

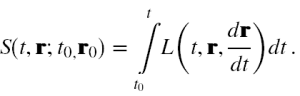
Całka jest wykonywana od początkowych położenia i chwili czasu, które są ustalone, do końcowych, które mogą być zmienne. Zakłada się, że funkcja Lagrange’a zależy od czasu oraz od zmiennych położeniowych i ich pochodnych po czasie, ale nie dowolnych, a tylko takich, które wynikają z rzeczywistych równań toru ruchu tego punktu. Zatem również i funkcja Z (11) dla ruchu klasycznego poprzez funkcję falową (7) i jej pochodne, zgodnie ze wzorem (8) zależy tylko od tych położeń i prędkości, które wynikają z toru ruchu tego punktu.

Wykonanie całki z funkcji Z po zmiennych x, y, z, ale nie po czasie t w sposób podany we wzorze (12) oznacza potraktowanie tych zmiennych jako zmiennych niezależnych.  Oznacza to założenie, że położenia x_j nie są już jednoznacznymi funkcjami czasu, nie są od niego już w ogóle zależne i mogą przyjmować dowolne wartości, a zatem nie opisują już toru ruchu cząstki. Takie postępowanie oznacza konieczność nadania szczegółowej, w tym oderwanej od pojęcia toru ruchu, interpretacji dla funkcji falowej ψ.

Literatura

1. Max Born, The statistical interpretation of quantum mechanics, Nobel Lecture, 1954.
2. Werner Heisenberg, Z. Physik, 33 (1925) 879.
3. Louis de Broglie, The wave nature of the electron, Nobel Lecture, 1929.
4. C.J. Davisson, L. H. Germer, Phys. Rev. 30, 707 (1927).
5. Erwin Schrödinger, Quantisation as a Problem of Proper Value, Part I, Annalen der Physik, 79 (1926) 361.
6. Erwin Schrödinger, Quantisation as a Problem of Proper Value, Part II, Annalen der Physik, 79 (1926) 489.
7. Erwin Schrödinger, Quantisation as a Problem of Proper Value, Part III, Annalen der Physik, 80 (1926) 437.
8. Erwin Schrödinger, Quantisation as a Problem of Proper Value, Part IV, Annalen der Physik, 81 (1926) 109.
9. W. Rubinowicz, W. Królikowski, Mechanika Teoretyczna, PWN, Warszawa 1978, rozdział III, §3.
10. I. M. Gelfand, S. W. Fomin, Rachunek Wariacyjny, PWN,Warszawa 1979, rozdział VII, §31.
11. R. S. Ingarden, A. Jamiołkowski, Mechanika Klasyczna, PWN, Warszawa-Poznań 1980, §15.1.